Proximal Algorithms 3 Interpretation

目录

• Moreau-Yosida regularization
• 与次梯度的联系
• 改进的梯度路径
• 信赖域问题

Proximal Algorithms

这一节，作者总结了一些关于proximal的一些直观解释

Moreau-Yosida regularization

内部卷积(infimal convolution)：

\[(f \: \Box \: g)(v)=\inf_x (f(x)+g(v-x))
\]

Moreau-Yosida envelope 或者 Moreau-Yosida regularization 为:

\[M_{\lambda f}=\lambda f \: \Box \: (1/2)\|\cdot\|_2^2
\]

， 于是:



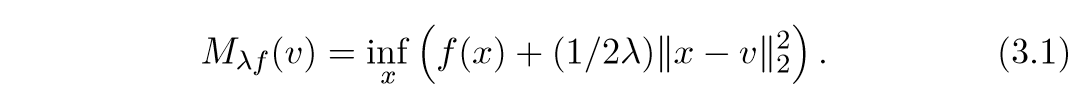
事实上，这就是，我们在上一节提到过的东西。就像在上一节一样，可以证明:

\[M_f (x) = f(\mathbf{prox}(x)) + (1/2) \|x-\mathbf{prox}_f(x)\|_2^2
\]

以及:

\[\nabla M_{\lambda_f}(x) = (1 / \lambda)(x- \mathbf{prox}_{\lambda f}(x))
\]

虽然上面的我不知道在\(f\)不可微的条件下怎么证明.

于是有与上一节同样的结果:



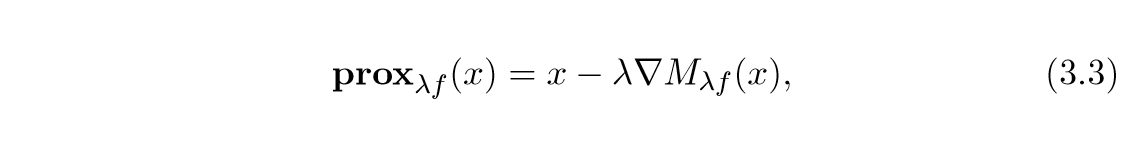
总结一下就是，近端算子，实际上就是最小化\(M_{\lambda f}\), 等价于\(\nabla M_{f^*}\)，即:

\[\mathbf{prox}_f(x) = \nabla M_{f^*} (x)
\]

这个，需要通过Moreau分解得到.

与次梯度的联系 \(\mathbf{prox}_{\lambda f} = (I + \lambda \partial f)^{-1}\)

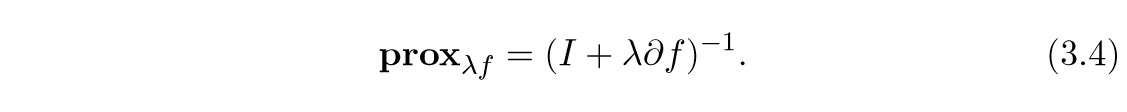
上面的式子，有一个问题是，这个映射是单值函数吗（论文里也讲，用关系来讲更合适），因为\(\partial f\)的原因，不过，论文的意思好像是的，不过这并不影响证明:

改进的梯度路径

就像在第一节说的，和之前有关Moreau envelope表示里讲的:

\[\mathbf{prox}_{\lambda f} (x) = x - \lambda \nabla M_{\lambda f}(x)
\]

实际上，\(\mathbf{prox}_{\lambda f}\)可以视为最小化Moreau envelope的一个迭代路径，其步长为\(\lambda\). 还有一些相似的解释.

假设\(f\)是二阶可微的,且\(\nabla^2 f(x) \succ0\)（表正定）,当\(\lambda \rightarrow 0\):

\[\mathbf{prox}_{\lambda f} (x) = (I + \lambda \nabla f)^{-1} (x) = x - \lambda \nabla f(x)+o(\lambda)
\]

这个的证明，我觉得是用到了变分学的知识:

\[\delta(I+\lambda \nabla f)^{-1}|_{\lambda=0}=-\frac{\nabla f}{(I+\lambda \nabla f)^{-2}}|_{\lambda =0}= -\nabla f
\]

所以上面的是一阶距离的刻画.

我们先来看\(f\)的一阶泰勒近似:

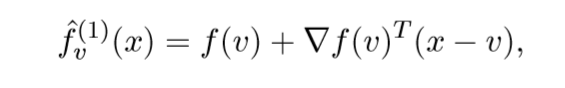
其近端算子为:



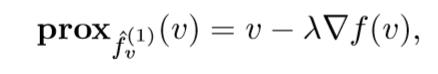
感觉，实际上是为:\(\mathbf{prox}_{\lambda \hat{f}_v^{(1)}}\)

相应的，还有二阶近似：

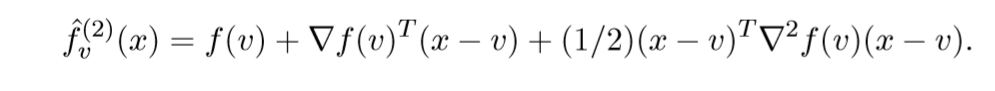
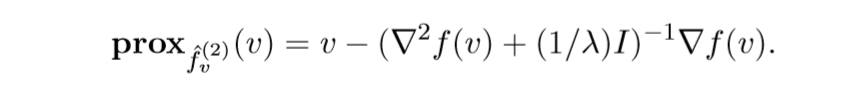
这个是Levenberg-Marquardt update的牛顿方法，虽然我不知道这玩意儿是什么.

上面的证明都是容易的，直接更具定义便能导出.

信赖域问题

proximal还可以用信赖域问题来解释:

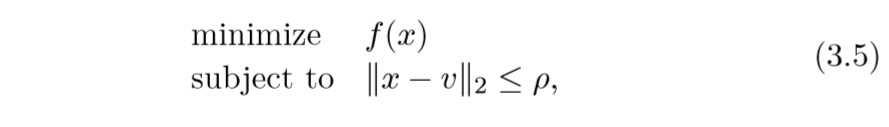
而普通的proximal问题：



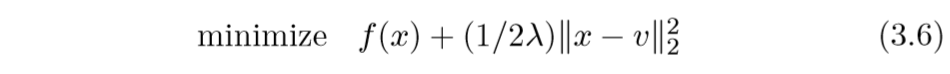
约束条件变成了惩罚项, 论文还指出，通过指定不同的参数\(\rho\)和\(\lambda\)，俩个问题能互相达到对方的解.