【数据结构与算法Python版学习笔记】树——二叉树的应用:解析树

解析树（语法树）

• 将树用于表示语言中句子， 可以分析句子的各种语法成分， 对句子的各种成分进行处理
• 语法分析树
• 程序设计语言的编译
  • 词法、语法检查
  • 从语法树生成目标代码
• 自然语言处理
  • 机器翻译
  • 语义理解

---

表达式解析

\(((7+3)*(5-2))\)

• 叶节点保存操作数，内部节点保存操作符
• 树中每个子树都表示一个子表达式

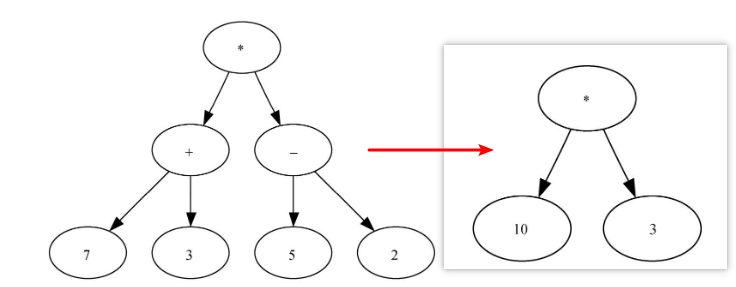
构建解析树

定义规则

• 如果当前标记是(，就为当前节点添加一个左子节点，并下沉至该子节点；
• 如果当前标记在列表['+', '-', '/', '＊']中，就将当前节点的值设为当前标记对应的运算符；为当前节点添加一个右子节点，并下沉至该子节点；
• 如果当前标记是数字，就将当前节点的值设为这个数并返回至父节点；
• 如果当前标记是)，就跳到当前节点的父节点。

步骤

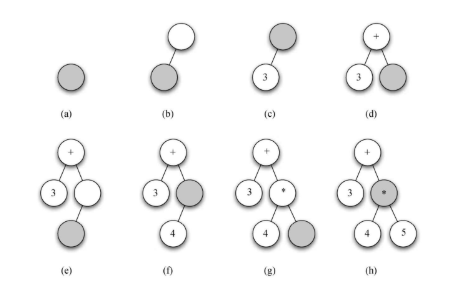
1. 创建一棵空树。
2. 读入第一个标记(。根据规则1，为根节点添加一个左子节点。
3. 读入下一个标记3。根据规则3，将当前节点的值设为3，并回到父节点。
4. 读入下一个标记+。根据规则2，将当前节点的值设为+，并添加一个右子节点。新节点成为当前节点。
5. 读入下一个标记(。根据规则1，为当前节点添加一个左子节点，并将其作为当前节点。
6. 读入下一个标记4。根据规则3，将当前节点的值设为4，并回到父节点。
7. 读入下一个标记＊。根据规则2，将当前节点的值设为＊，并添加一个右子节点。新节点成为当前节点。
8. 读入下一个标记5。根据规则3，将当前节点的值设为5，并回到父节点。
9. 读入下一个标记)。根据规则4，将＊的父节点作为当前节点。
10. 读入下一个标记)。根据规则4，将+的父节点作为当前节点。因为+没有父节点，所以工作完成。

思路

• 创建左右子树可调用insertLeft/Right
• 当前节点设置值，可以调用setRootVal
• 下降到左右子树可调用getLeft/RightChild
• 上升到父节点，这个没有方法支持，用一个栈来记录跟踪父节点
  • 当前节点下降时，将下降前的节点push入栈
  • 当前节点需要上升到父节点时，上升到pop出栈的节点即可！

代码

class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def push(self, item):  # 将item加入栈顶，无返回值
        return self.items.append(item)
    def pop(self):  # 将栈顶数据项移除，并返回，栈被修改
        return self.items.pop()
    def peek(self):  # "窥视"栈顶数据项，返回栈顶的数但不移除，栈不被修改
        return self.items[len(self.items)-1]
    def size(self):
        return len(self.items)
class BinaryTree:
    def __init__(self, rootObj):
        self.key = rootObj
        self.leftChild = None
        self.rightChild = None
    def insertLeft(self, newNode):
        if self.leftChild == None:
            self.leftChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.leftChild = self.leftChild
            self.leftChild = t
    def insertRignt(self, newNode):
        if self.rightChild == None:
            self.rightChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.rightChild = self.rightChild
            self.rightChild = t
    def getRightChild(self):
        return self.rightChild
    def getLeftChild(self):
        return self.leftChild
    def setRootVal(self, obj):
        self.key = obj
    def getRootVal(self):
        return self.key
def buildParseTree(fpexp):
    fplist = fpexp.split()
    pstack = Stack()
    eTree = BinaryTree('')
    # 入栈下降
    pstack.push(eTree)
    currentTree = eTree
    for i in fplist:
        # 表达式开始
        if i == '(':
            currentTree.insertLeft('')
            pstack.push(currentTree)  # 入栈下降
            currentTree = currentTree.getLeftChild
        elif i not in ['+', '-', '*', '/', ')']:
            currentTree.setRootVal(int(i))
            parent = pstack.pop()  # 出栈上升
            currentTree = parent
        elif i in ['+', '-', '*', '/']:
            currentTree.setRootVal(i)
            currentTree.insertRignt('')
            pstack.push(currentTree)
            currentTree = currentTree.getRightChild()
        elif i == ')':
            currentTree = pstack.pop()  # 出栈上升
        else:
            raise ValueError
    return eTree

---

表达式解析树求值

• 由于二叉树BinaryTree是一个递归数据结构， 自然可以用递归算法来处理

• 求值函数evaluate的递归三要素

  • 基本结束条件：叶节点是最简单的子树，没有左右子节点，其根节点的数据项即为子表达式树的值
  • 缩小规模：将表达式树分为左子树、右子树，即为缩小规模
  • 调用自身：分别调用evaluate计算左子树和右子树的值，然后将左右子树的值依根节点的操作符进行计算，从而得到表达式的值

• 一个增加程序可读性的技巧：函数引用

  import operator
  op= operator.add
  

代码

def evaluate(parseTree):
    opers = {
        '+': operator.add,
        '-': operator.sub,
        '*': operator.mul,
        '/': operator.truediv
    }
    # 缩小规模
    leftC = parseTree.getLeftChild()
    rightC = parseTree.getRightChild()
    if leftC and rightC:
        fn = opers[parseTree.getRootVal()]
        # 递归调用
        return fn(evaluate(leftC), evaluate(rightC))
    else:
        # 基本结束条件
        return parseTree.getRootVal()