LeetCode1240铺瓷砖

题目

n*m的矩阵，只用正方形铺。求最少正方形个数。

n，m<=13

思路

贪心：

加入是最大的正方形，显然行不通，比如n=11,m=13。那么贪心策略是1个11，其余是大小为2的正方形5个，大小为1的两个。一共1+5+2=8个。

然而正确答案是7一个，6一个，5一个，4两个，1一个，共6个。

DP：

直接尝试所有方案：

f(n,m)

if(n=m) 返回1.

if(n=1||m=1)返回不等于1的。

if(n小于m) 交换n,m//使得n>=m

如果memo中计算过，则直接返回。

for(i=[1,m]）

在左上角放入大小为i的正方形。那么剩下来的部分有两种方法：以正方形的两条线把矩阵分割成一共三个部分。

f(m-i,n)+f(i,n-i)或者f(n-i,m)+f(m-i,i)。这两种方案取小者。

上面的思路是错误，对于下面的形式不能适用。

普通形式应该是上图这样的。之前的形式是上图的特殊情况。

以中间的矩形为观测中心，矩形上界为i1,下界为i2，左界为j1，右界为j2。因为是左上角是正方形，所以j1=i2.

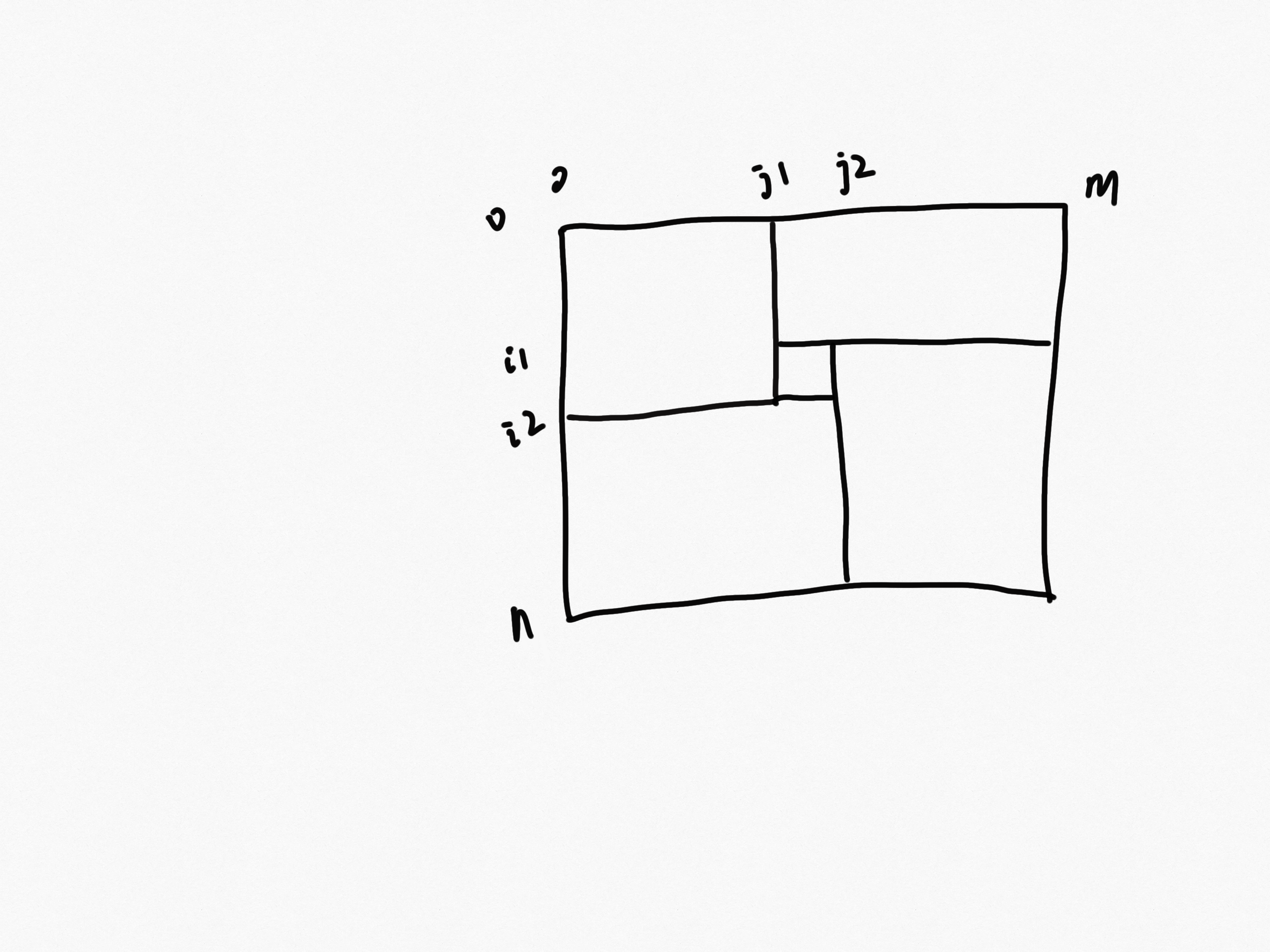
实现手段用DP即可。计算f(n,m)时，只依赖于参数小于n、m的值。

递推公式：

f(n,m)=1+f(i2-i1,j2-j1)中间的+f(i1,m-j1)右上角的+f(n-i2,j2)左下角+f(n-i1,m-j2)

其中j1=i2，因为左上角是正方形。

1<=i1<=i2<=n;j1<=j2<=m，遍历这些值取最小值即可。

出口：m==n时，直接返回1.n或者m有一个为0时，返回0，代表有线重合，是某种特殊情况。

public int tilingRectangle(int n, int m) {
    int[][] dp = new int[n + 1][m + 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {//dp[i][j]=dp[j][i]
            dp[i][j] = getRes(dp, i, j);
        }
    }
    return dp[n][m];
}

/**
 * @param dp
 * @param n
 * @param m
 * @return
 */
private int getRes(int[][] dp, int n, int m) {
    if (n == m) {
        return 1;
    }
    int min = Integer.MAX_VALUE;
    for (int i1 = 1; i1 <= n; i1++) {
        for (int i2 = i1; i2 <= n; i2++) {
//                for (int j1 = 1; j1 <= m; j1++) {//左上角正方形,j1=i2
            int j1 = i2;
            for (int j2 = j1; j2 <= m; j2++) {
                int tmpRes = 1 + dp[n - i2][j2] + dp[i1][m - j1] + dp[n - i1][m - j2] + dp[i2 - i1][j2 - j1];
                min = Math.min(tmpRes, min);
            }

        }

    }
    return min;
}