[学习笔记] IT项目管理 - 关键路径法

关键路径法

只有项目网络中最常的或者耗时最多的活动完成之后，项目才能结束，这条最长的活动路线就叫关键路径。组成关键路径的活动称为关键活动。

图形表示

最早开始时间ES	工期Duration	最早结束时间EF
	活动ID
最晚开始时间LS	浮动时间Slack	最晚结束时间LF

其中浮动时间Slack = LS - ES 或 LF - EF

例子

工作代号	紧前工作	工期
A		5
B	A	2
C	A	8
D	B、C	10
E	C	5
F	D	10
G	D、E	15
H	F、G	10

画出工序图

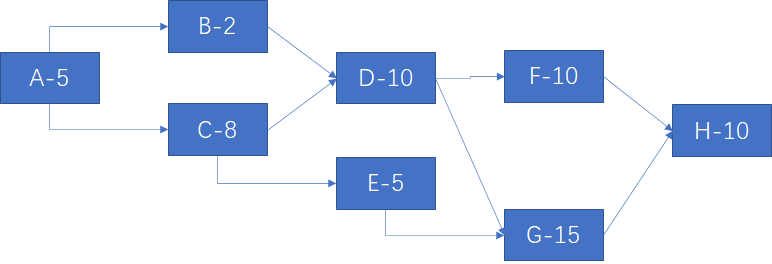
加入最早时间

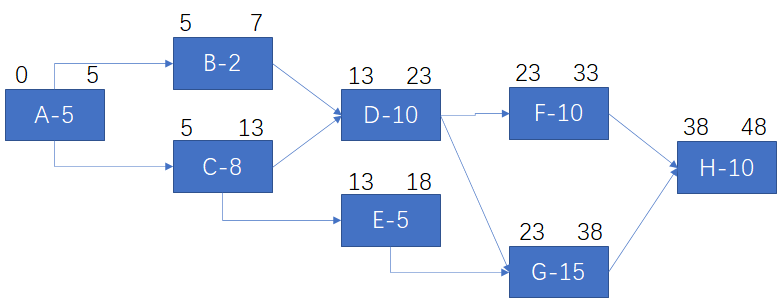
加入最晚时间

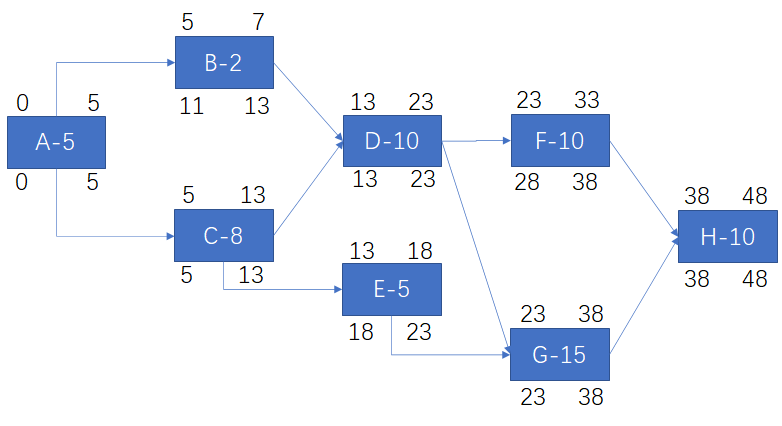
浮动时间：B:6, E:5, F:5

关键路径：A-C-D-G-H

总时差（TF）

当一项活动的最早开始时间和最迟开始时间不相同时，它们之间的差值是该工作的总时差。计算公式是：TF=LS-ES。

总时差：B:6, E:5, F:5

自由时差（FF）

在不影响紧后活动完成时间的条件下，一项活动可能被延迟的时间是该项活动的自由时差，它由该项活动的最早完成时间EF和它的紧后活动的最早开始时间决定的。计算公式是：FF=min{后一活动ES}-EF。

自由时差：B:6, E:5, F:5

干扰时差

和紧后工作共用的时间，其实就是占用了后续工作的自由时差。

总时差 = 自由时差 + 干扰时差