UVA10079 Pizza Cutting 题解

Content

求用 \(n\) 条直线最多能将平面分成多少块区域。

多组输入，以一个负数结束。

数据范围：\(0\leqslant n\leqslant 2.1\times 10^8\)。

Solution

小学奥数题。

首先你得要知道 \(1+2+...+n=\dfrac{n(n+1)}{2}\)。

我们先通过画图来找一下规律。

• 不切，此时很显然总共有 \(1\) 个区域。

• 切一刀，此时最多有 \(2\) 个区域。

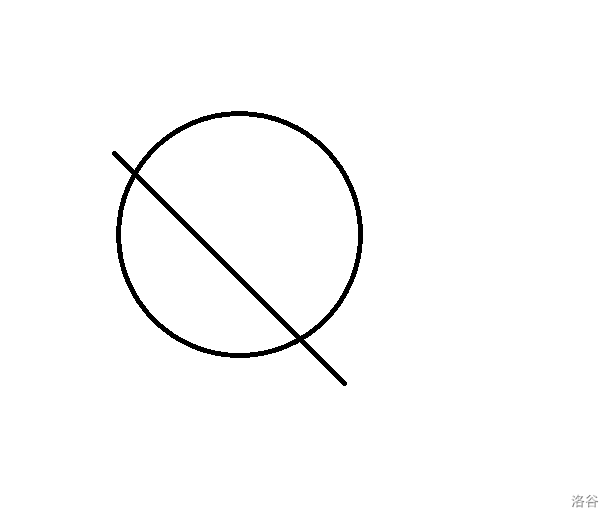
• 切两刀，此时最多有 \(4\) 个区域。

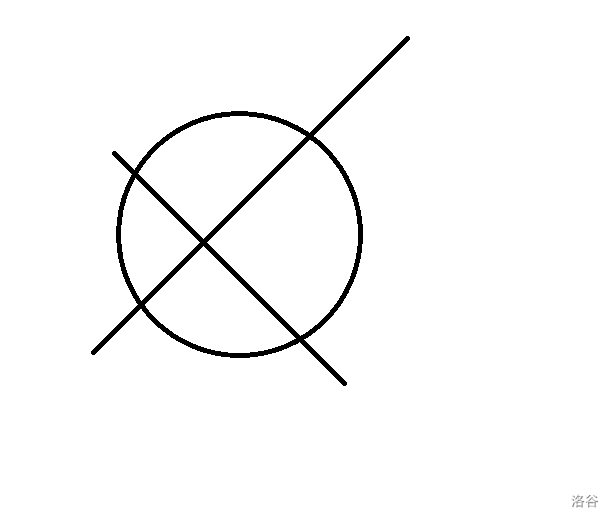
• 切三刀，此时最多只能有 \(7\) 个区域。

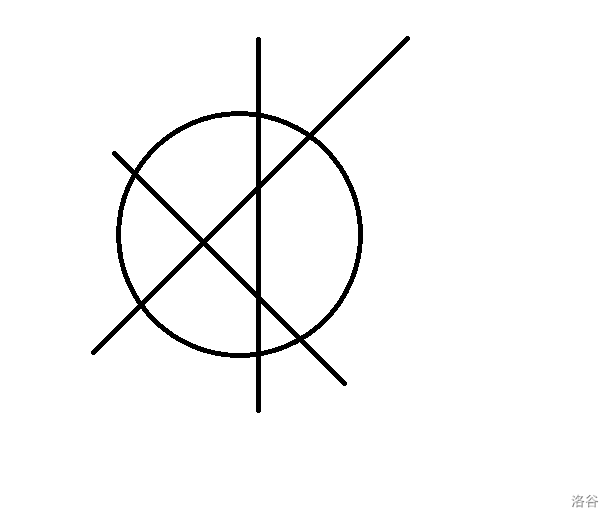
为什么呢？

因为第三条直线最多只能和前面的直线有 \(2\) 个交点，这样直线就分成了三个部分，因此最多只能够新产生 \(3\) 个区域。

类似的，第 \(n\) 条直线最多只能和前面的直线有 \((n-1)\) 个交点，把直线分成 \(n\) 个部分，最多只能够新产生 \(n\) 个区域。

故，\(n\) 条直线最多能将平面分成：\(1+1+2+...+n=1+\dfrac{n(n+1)}{2}\) 个区域。

注意这么大的答案如果只开 \(\texttt{int}\) 的话是肯定要爆的，因此得开 \(\texttt{long long}\)。

Code

#include <cstdio>
#include <algorithm>
using namespace std;

long long n;

int main() {
	while(~scanf("%lld", &n) && n >= 0)
		printf("%lld\n", n * (n + 1) / 2 + 1);
}