[HEOI2014]逻辑翻译

ywy_c_asm的良心题解

是道好题

体现了二进制位的形象递归思想，以及将FWT的思路（都是拆位分治）用到题目中的典范

可以暴力高斯消元。完全没有利用2^N以及+-1的良好性质

发现项数，方程和二进制位有关系

考虑类似FWT，FFT能不能递归？

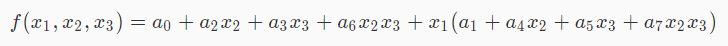
已经具备递归的模式

但是怎样递归下去？
消掉x1的话，对应的位置，1010,0010，相加除以2，相减除以2，分别作为两边递归下去的答案，即可。

这样，通过化简规模，最终到了边界就可以直接得到解。

细节比较多

1.我是+用1，-用0，选择1用1，选择0用0，最后使得项数下标和最后选择的方程下标一致，直接得到答案

2.输出恶心，还是分治。注意别重复输出。其实写的好看一点，本质是线段树的x<<1,x<<1|1

3.读入double，不要强转int，可能是0.999999999999999,所以，x=round(100*df)，四舍五入即可。

4.为了卡常，必须快输。

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
int n;
int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}
struct node{
    int u,d;
    node(){}
    node(ll s,ll m){
        u=s;d=m;
    }
    node friend operator +(node a,node b){
        return node(a.u+b.u,a.d);
    }
    node friend operator -(node a,node b){
        return node(a.u-b.u,a.d);
    }
    node friend operator *(node a,ll b){
        return node(a.u*b,a.d);
    }
    node friend operator /(node a,ll b){
        return node(a.u,a.d*b);
    }
    void op(){
        if(u<) putchar('-'),u=-u;
        int g=gcd(u,d);
        u/=g;d/=g;
        printf("%d",u);
        if(d!=) printf("/%d",d);
    }
}c[<<];//,f[1<<20],g[1<<20];
char s[];
void get(){
    scanf("%s",s);
    int to=;
    for(reg i=;i<n;++i){
        if(s[i]=='+') to+=(<<i);
    }
    double df;
    scanf("%lf",&df);
    c[to].d=;c[to].u=round(df*100.0);
}
void div(int l,int r,int to,int cnt){
    if(cnt==n){
        //f[to]=c[to];
        return;
    }
    int mid=(l+r)>>;
    for(reg i=;i<(<<(n-cnt-));++i){
        int t1=(i<<(cnt+))|(to)|(<<cnt);
        int t0=(i<<(cnt+))|(to);//|(1<<cnt)
        node tmp=c[t1];
        c[t1]=(tmp-c[t0])/;
        c[t0]=(tmp+c[t0])/;
    }
    div(l,mid,to,cnt+);
    div(mid+,r,to|(<<cnt),cnt+);
}
bool has[<<];
void op(int s){
    if(has[s]) return;
    has[s]=;
    if(c[s].u==) return;
    c[s].op();
    putchar(' ');
    for(reg i=;i<n;++i){
        if(s&(<<i)){
            printf("x%d",i+);
        }
    }
    puts("");
}
void out(int l,int r,int to,int cnt){
    if(cnt==n-){
        op(to);op(to|(<<cnt));op(to|(<<cnt)|(<<(cnt+)));op(to|(<<(cnt+)));
        return;
    }
    if(!has[to])op(to);
    int mid=(l+r)>>;
    out(l,mid,to|(<<cnt),cnt+);
    out(mid+,r,to,cnt+);
}
int main(){
    rd(n);
    for(reg i=;i<(<<n);++i) get();
//    for(reg i=0;i<(1<<n);++i){
//        cout<<c[i].u<<" "<<c[i].d<<endl;
//    }
    div(,(<<n)-,,);
    if(n==){
        op();op();return ;
    }
    out(,(<<n)-,,);
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2019/1/11 19:21:58
*/