Beta Distribution

首先思考一个问题：

熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average)，就是用一个运动员击中的球数除以击球的总数，我们一般认为0.266是正常水平的击球率，正常范围在0.215到0.36，而如果击球率高达0.3就被认为是非常优秀的。

现在有一个棒球运动员，我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率，用击中的数除以击球数，但是如果这个棒球运动员只打了一次，而且还命中了，那么他就击球率就是100%了，这显然是不合理的，因为根据棒球的历史信息，我们知道这个击球率应该是0.215到0.36之间才对啊。

在这种具有先验知识的情况下，一种考虑可能是贝叶斯，但是击球命中与否是对立事件，贝叶斯用于描述两个事件之间的因果关系。这种已有先验知识，再去更新统计数据的情况，Beta Distribution可能是最佳选择了。

B分布的理解和使用不需要考虑其数学定义，B分布定义在(0, 1)，用B(x; α, β) 表示，其中x是自变量，α, β是hyperparameter，给出α, β就可以确定其形状。

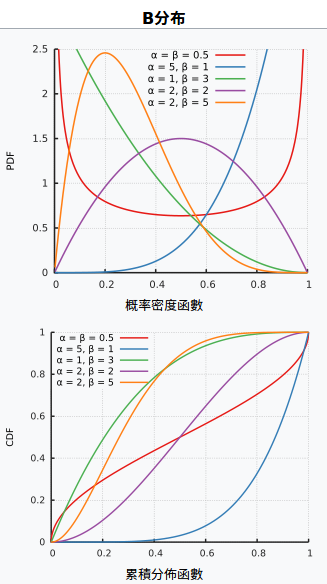
B分布有一些很实用的性质：其众数、期望、方差、偏差、峰度等分布特征都由α, β确定；当初始参数α, β确定以后，可以在先验的基础上开始统计，并更新概率分布。回到最开始的问题。

对于这个问题，我们可以用一个二项分布表示（一系列成功或失败），一个最好的方法来表示这些经验（在统计中称为先验信息）就是用beta分布，这表示在我们没有看到这个运动员打球之前，我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。

接下来我们将这些先验信息转换为beta分布的参数，我们知道一个击球率应该是平均0.27左右，而他的范围是0.21到0.35，那么根据这个信息，我们可以取α=81,β=219。

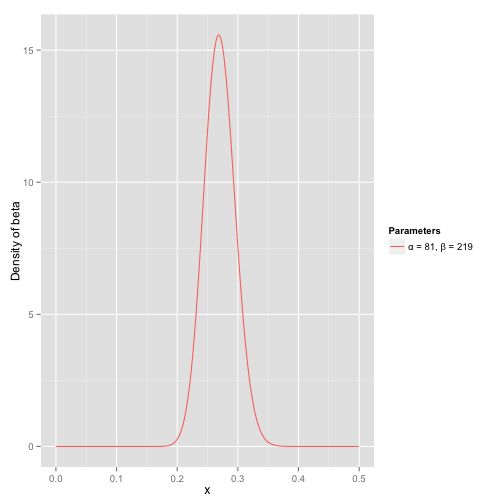
之所以取这两个参数是因为：

• beta分布的均值是
• 从图中可以看到这个分布主要落在了(0.2,0.35)间，这是从经验中得出的合理的范围。

在这个例子里，我们的x轴就表示各个击球率的取值，x对应的y值就是这个击球率所对应的概率。也就是说beta分布可以看作一个概率的概率分布。

那么有了先验信息后，现在我们考虑一个运动员只打一次球，那么他现在的数据就是”1中;1击”。这时候我们就可以更新我们的分布了，让这个曲线做一些移动去适应我们的新信息。beta分布在数学上就给我们提供了这一性质，他与二项分布是共轭先验的（Conjugate_prior）。所谓共轭先验就是先验分布是beta分布，而后验分布同样是beta分布。结果很简单：

这个新的B分布的数学期望，可以认为是该运动员最新的命中率。