P2149 [SDOI2009]Elaxia的路线

题目描述

最近，Elaxia和w**的关系特别好，他们很想整天在一起，但是大学的学习太紧张了，他们必须合理地安排两个人在一起的时间。

Elaxia和w**每天都要奔波于宿舍和实验室之间，他们希望在节约时间的前提下，一起走的时间尽可能的长。

现在已知的是Elaxia和w**所在的宿舍和实验室的编号以及学校的地图：地图上有N个路口，M条路，经过每条路都需要一定的时间。具体地说，就是要求无向图中，两对点间最短路的最长公共路径。

输入输出格式

输入格式：

第一行：两个整数N和M（含义如题目描述）。

第二行：四个整数x1、y1、x2、y2（1 ≤ x1 ≤ N，1 ≤ y1 ≤ N，1 ≤ x2 ≤ N，1 ≤ y2 ≤ N），分别表示Elaxia的宿舍和实验室及w**的宿舍和实验室的标号（两对点分别 x1,y1和x2,y2）。

接下来M行：每行三个整数，u、v、l（1 ≤ u ≤ N，1 ≤ v ≤ N，1 ≤ l ≤ 10000），表 u和v之间有一条路，经过这条路所需要的时间为l。

输出格式：

一行，一个整数，表示每天两人在一起的时间（即最长公共路径的长度）

输入输出样例

输入样例#1：
复制

输出样例#1： 复制

说明

对于30%的数据，N ≤ 100；

对于60%的数据，N ≤ 1000；

对于100%的数据，N ≤ 1500，输入数据保证没有重边和自环。

可证最优解一定是连续的一段，因为两点间的最短路是一定的，所以最优解如果有一段不连续的话两个人走的不相同的两段路的长度也一定相同，也就是说其实可以走一起走一样的路而不用分开走以获得更优解

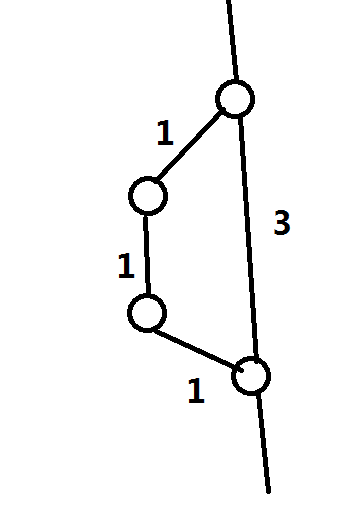
所以要找的就是同时在两条最短路上的最长的连续重合路径

思路：找出每一条同时在两条最短路上的边，最长的连续段即为所求。

方法：

1.从x1,x2,y1,y2跑4遍spfa

2.穷举每一条边，如果这条边边长+边的一边到x1的距离+另一边到y1的距离=x1到y1的距离同时x2到y2也符合上述条件则此边在两条最短路上，把此边加入集合

3.重新建图注意这次要建单向边！！ 也就是说只有当一条边在x1到y1的路径上而不是在y1到x1的路径上时才把此边加入

4.从新建的图上找出最长的连续段即为所求

#include<iostream>

#include<stdio.h>

#include<queue>

#include<cstring>

using namespace std;

queue<int> q;

int i,m,n,j,k,a[1501][1501],ver[2500001],nex[2500001],head[100001],x[2],y[2],u,v,l,edge[2500001];

int maxx,cnt,fr[2500001],mm[1501];

bool b[1501][1501];

inline int getint()

{

    char ch;

    int res=0;

    while(ch=getchar(),ch<'0'||ch>'9');

    res=ch-48;

    while(ch=getchar(),ch>='0'&&ch<='9')

    res=(res<<3)+(res<<1)+ch-48;

    return res;

}

void add(int x,int y,int z)

{

    cnt+=1;

    ver[cnt]=y;

    nex[cnt]=head[x];

    head[x]=cnt;

    edge[cnt]=z;

    fr[cnt]=x;

}

int spfa(int x)

{

    while(q.size()) q.pop();

    q.push(x);

    a[x][x]=0;

    while(q.size())

    {

        int t=q.front();

        q.pop();

        for(int i=head[t];i;i=nex[i])

        {

            int r=ver[i];

            if(a[x][r]>a[x][t]+edge[i])

            {

                a[x][r]=a[x][t]+edge[i];

                q.push(r);

            }

        }

    }

}

void tp(int x,int f)

{

    for(int i=head[x];i;i=nex[i])

    {

        int t=ver[i];

        if(t==f) continue;

        if(mm[x]+edge[i]>mm[t])

        {

            mm[t]=mm[x]+edge[i];

            maxx=max(maxx,mm[t]);

            tp(t,x);

        }

    }

}

int main()

{

    n=getint(); m=getint(); x[0]=getint(); y[0]=getint(); x[1]=getint(); y[1]=getint();

    for(i=1;i<=m;i++)

    {

        u=getint(); v=getint(); l=getint();

        add(u,v,l);

        add(v,u,l);

    }

    memset(a,0x3f,sizeof(a));

    spfa(x[0]); spfa(x[1]); spfa(y[0]); spfa(y[1]);

    k=cnt; cnt=0; memset(head,0,sizeof(head));

    for(i=1;i<=k;i++)

    {

        if((a[x[0]][fr[i]]+edge[i]+a[y[0]][ver[i]]==a[x[0]][y[0]])&&(a[x[1]][fr[i]]+edge[i]+a[y[1]][ver[i]]==a[x[1]][y[1]]))

            add(fr[i],ver[i],edge[i]);

        else if((a[x[0]][fr[i]]+edge[i]+a[y[0]][ver[i]]==a[x[0]][y[0]])&&(a[x[1]][ver[i]]+edge[i]+a[y[1]][fr[i]]==a[x[1]][y[1]]))

            add(fr[i],ver[i],edge[i]);

    }

    for(i=1;i<=cnt;i++)    if(mm[fr[i]]==0) tp(fr[i],0);

    printf("%d",maxx);

}

ps.依然坚持认为我写的跑n遍dijkstra的n²logn的时间复杂度挺好的（我才不会承认它确实只能得28分QAQ