一:线性dp

概念：

动态规划是运筹学的一个分支，是求解决策过程最优化的数学方法。

动态规划是通过拆分问题，定义问题状态和状态之间的关系使得问题能够以递推（或者说分治）的方法去解决。

解决策略：

1）最优化原理：如果问题的最优解包含的子问题的解也是最优的，就称该问题又最有子结构，既满足最优化原理。

2）无后效性：某阶段状态一旦确定，就不受这个状态以后的决策影响。也就是说，某状态以后的过程不会影响以前的状态，至于当前状态有关。

3）有重叠子问题：即子问题之间不是独立的，一个字问题在下一阶段决策中可能多次被用到。（该性质并不是动态规划的必要条件，但如果没有这条性质，

　　动态规划算法和其他算法相比就不具备优势）

解决问题步骤：

1.拆分问题

　  　把原问题分解为若干个子问题，子问题和原问题形式相同或类似，只不过规模变小了。子问题都解决，原问题即解决(数字三角形例）。

　　 子问题的解一旦求出就会被保存，所以每个子问题只需求 解一次。

2.找状态（初始值）

　　  在用动态规划解题时，我们往往将和子问题相关的各个变量的一组取值，称之为一个“状 态”。一个“状态”对应于一个或多个子问题， 所谓某个“状态”下的“值”，就是这个“状 态”所对应的子问题的解。

　　  所有“状态”的集合，构成问题的“状态空间”。“状态空间”的大小，与用动态规划解决问题的时间复杂度直接相关。

　　 整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。在数字三角形里每个“状态”只需要经过一次，且在每个状态上作计算所花的时间都是和N无关的常数。

　　还需要确定一些（初始状态）边界状态的值。

3.状态转移方程

其实动态规划就好比中学时候学的通项公式，找到这个通项公式之后每次递推就可以取得最后的结果。

用动态规划能写的题基本上用递归的方法都可以。

　　递归到动规的一般转化方法

　　　　 递归函数有n个参数，就定义一个n维的数组，数组的下标是递归函数参数的取值范围，数组元素的值是递归函数的返回值，这样就可以从边界值开始， 逐步填充数组，相当于计算递归函数值的逆过程。

　　

 1.最长上升子序列

　　子序列：字符的子序列指的是从给定的字符序列中随意的（不一定连续）的曲调若干个字符（也可能一个也不去掉）最后形成的字符序列。

　eg:

给你一个长度为n的序列，求其最长上升子序列。

//*****LIS

#include<bits/stdc++.h>
using namespace std;
int a[10010];
int dp[10010];
int main()
{
　　int n;

　　while(cin>>n&&n)
　　{
　　for(int i=0;i<n;i++)
　　{
　　　　cin>>a[i];
　　　　dp[i]=1;
　　}
　　int ans=0;
　　for(int i=1;i<n;i++)
　　{
　　　　for(int j=0;j<i;j++)
　　　　　　if(a[j]<a[i])
　　　　　　　　dp[i]=max(dp[j]+1,dp[i]);
　　
　　　　ans=max(ans,dp[i]);
　　}
　　　cout<<ans<<endl;
　　}
　　return 0;
}

//2 5 3 7 4 2

推荐题目链接：http://acm.nyist.edu.cn/JudgeOnline/problem.php?pid=17

2.求最长上升子序列的长度

//*****LIS nlogn

#include<bits/stdc++.h>
using namespace std;
const int INF=9999999;
int dp[100];//dp[i]表示长度为i+1的子序列末尾元素最小值；
int a[100];
int main()
{
　　int n;
　　while(cin>>n&&n)
　　{
　　for(int i=0;i<n;i++)
　　{
　　　　cin>>a[i];
　　　　dp[i]=INF;
　　}
　　for(int i=0;i<n;i++)
　　　　*lower_bound(dp,dp+n,a[i])=a[i];//找到>=a[i]的第一个元素，并用a[i]替换；
　　

　　cout<<lower_bound(dp,dp+n,INF)-dp<<endl;//找到第一个INF的地址减去首地址就是最大子序列的长度；
　　}
　　return 0;

}

/*
2 1 5 3 6 4 8 9 7
1 3 4 7 9
1 2 3 4 5
1 3 4 7 9
*/

3.最长公共子序列

题目链接：http://acm.nyist.edu.cn/JudgeOnline/problem.php?pid=36

大意：给两个字符串，要求求出最长的公共子序列，求出的公共子序列在每个给定的字符串中可不连续

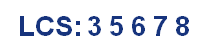
//*******LCS

#include<bits/stdc++.h>
using namespace std;

string s1,s2,s3;
][];
int len1,len2;
int main()
{
    while(cin>>s1>>s2)
    {
        memset(dp,,sizeof(dp));
        len1=s1.length();
        len2=s2.length();
        ; i<len1;i++)
            ; j<len2;j++)
            {
                if(s1[i]==s2[j])
                    dp[i+][j+]=dp[i][j]+;
                else
                    dp[i+][j+]=max(dp[i+][j],dp[i][j+]);
            }
        cout<<dp[len1][len2]<<endl;
    }
    ;
}

最后推荐两个写dp的博客：

https://blog.csdn.net/baidu_28312631/article/details/47418773

https://blog.csdn.net/baidu_28312631/article/details/47426445