题解 p2017 [USACO09DEC]晕牛Dizzy Cows

前言：P大终于又更新了

正文

转送门

由于当时我这个ZZ不知怎么了，这份题解排版可能有些尴尬，建议大家读完题后，看我主程序前的代码的注释，然后看最下面的图片，然后看第一张图片，对不起，望多谅解

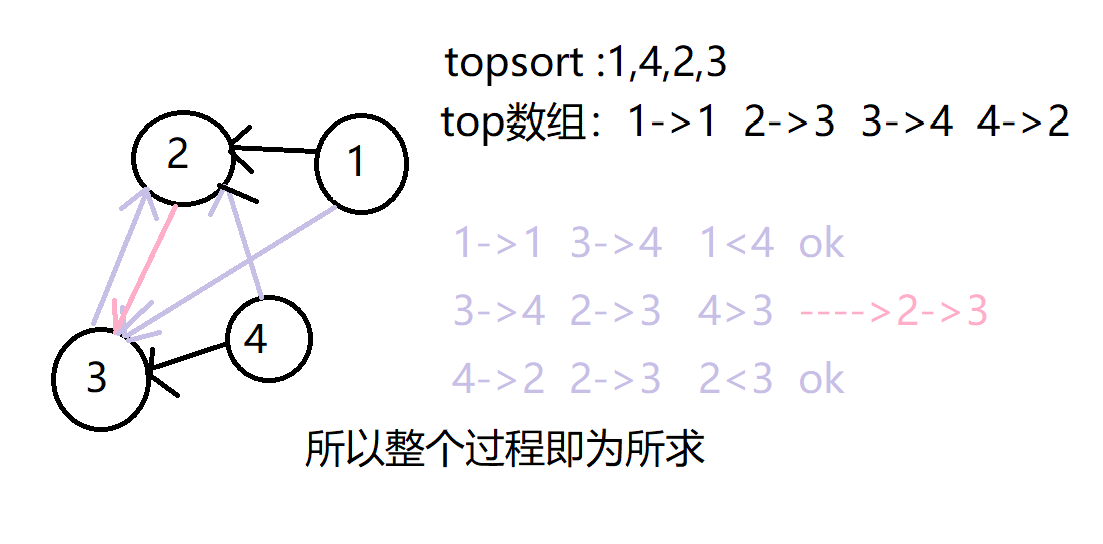
以样例为例。具体看代码及其中的注释，这样做的正确性，看最下面说明

#include<iostream>#include<cstdio>#include<queue>using namespace std;/*    晕牛：拓扑排序    根据题干可知，有向边不成环，所以通过拓扑排序可以知道哪个入度少    当你强行把拓扑排序后在排序位置前面的点a和排序在后面的点b链接这一起    形成一条从b到a的有向边，则就会形成环。    而未避免形成环，就要在后面读入无向图时进行判断     而此题由于无向图的双向性不好处理，    于是，就规定输入第一个数字为出度，第二个数字为入度     先把不会形成环的点跑一个拓扑排序    然后在判断让某些点强行连接后会不会有环    会就改方向，不会就不用管 */const int MAXN=100001;int tot,a,b,n,p1,p2,cnt;int top[MAXN];//top是拓扑排序后每个数的编号 int head[MAXN],ver[MAXN],nxt[MAXN],deg[MAXN];//存图 void add(int x,int y){    ver[++tot]=y;nxt[tot]=head[x];    head[x]=tot;deg[y]++;}void topsort(){//拓扑排序     queue<int> q;    for(register int i=1;i<=n;i++)        if(deg[i]==0) q.push(i),top[i]=++cnt;    //先扫一遍，把初始就没有入度的排序     while(q.size()){        int x=q.front();q.pop();        for(register int i=head[x];i;i=nxt[i]){            int y=ver[i];            //y是该到某个边的出度点了             if(!(--deg[y])) q.push(y),top[y]=++cnt;            //如果它入度为零的话，就把它塞进栈里         }    }}int main(){    scanf("%d%d%d",&n,&p1,&p2);    for(register int i=1;i<=p1;i++)        scanf("%d%d",&a,&b),add(a,b);    topsort();    for(register int i=1;i<=p2;i++){        scanf("%d%d",&a,&b);        if(top[a]>top[b]) printf("%d %d\n",b,a);        //如果在原本拓扑排序中a的序列在b后面，强行连一条从a到b的边，会有环         else printf("%d %d\n",a,b);    }    return 0;}

说明

 

国际惯例：thankyou for your attention