[机器学习] SVM——Hinge与Kernel

Support Vector Machine

[学习、内化]——讲出来才是真的听懂了，分享在这里也给后面的小伙伴点帮助。
learn from:
https://www.youtube.com/watch?v=QSEPStBgwRQ&list=PLJV_el3uVTsPy9oCRY30oBPNLCo89yu49&index=29
台湾大学李宏毅教授，讲授课程很用心，能把我之前看过却不理解的知识很易懂、精彩的讲出来——respect

1、SVM

SVM是一个经典的二分类、监督学习算法。与logistic regression很像（需要先学此基础），主要独特之处有两点：

1.loss fuction 用 Hinge Loss。

2.模型 f(x) 使用了 kernel method。

下面依次理解这两个关键，来学习SVM。

2、Hinge Loss

2.1

SVM 算法结构与 logistic regression 或者 binary classification 基本一样：

在解决上面原L(f)不能做梯度下降时，与logistic regression使用 sigmoid + cross entropy不同，使用Hinge Loss，从而产生了Linear SVM。

Hinge：

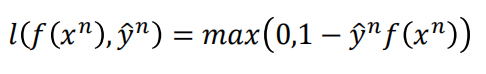
logistic regression 与 Linear SVM两个算法唯一的不同之处就是使用了不同的loss function,前者使用的sigmoid+cross，而后者用 hinge 。

2.2

下面讲讲 loss function 那些事，理解这些后，将对 SVM 的 HInge 有很深的理解。
因为原本的loss fuction（下图中标①的loss function，下文简称L①）不能微分所以无法做梯度下降 ，所以我们要做的就是用一个可以微分的loss function（下文简称L②）来近似代替L①。我们知道L①的作用：当预测值与实际值相等时，L=0，不相等时，L=1（函数括号里成立时，函数值=0，否则为1，不清楚的可以查一下 kronecker 记号）。binary classification 中:

而y只等于+1或-1，所以预测正确时，即g(x)与y相等时，y一定与f(x)同号，预测错误时异号。（以0点为界，y·f(x)越大即就是预测正确，y·f(x)越小即为预测错误，下图中用yf(x)作图分析并说Larger value, smaller loss，应该是这样理解的）所以我们需要找这样一个L②来代替L①：当同号时，loss接近0；当异号时，loss很大。

下面是尝试使用不同的L②：

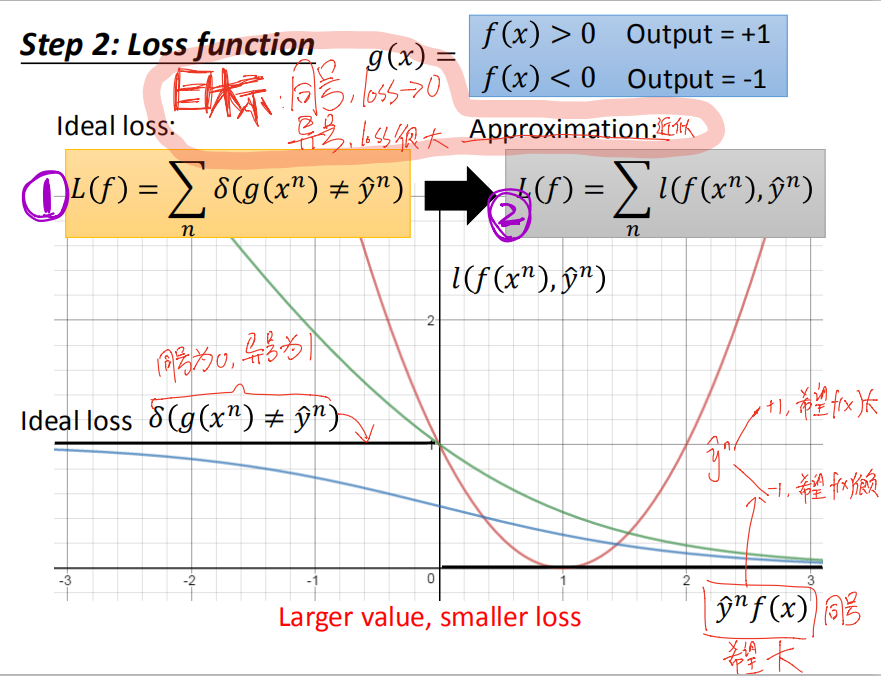
square loss: 不行。

连我们上面分析L②应有的性质都不满足，而已早在 logistic regression 里就知道了 square loss 是不适用这种离散型任务的。

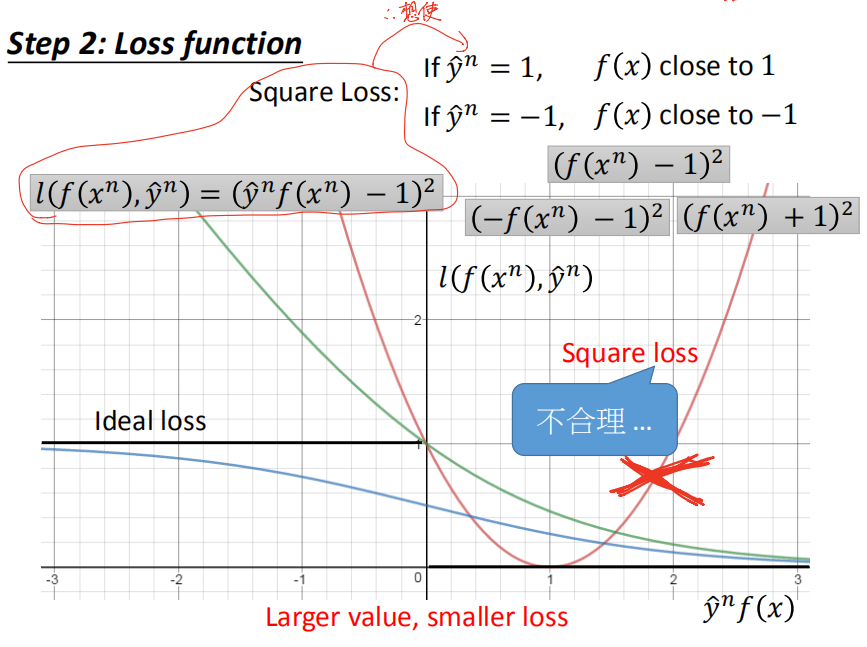
sigmoid+square

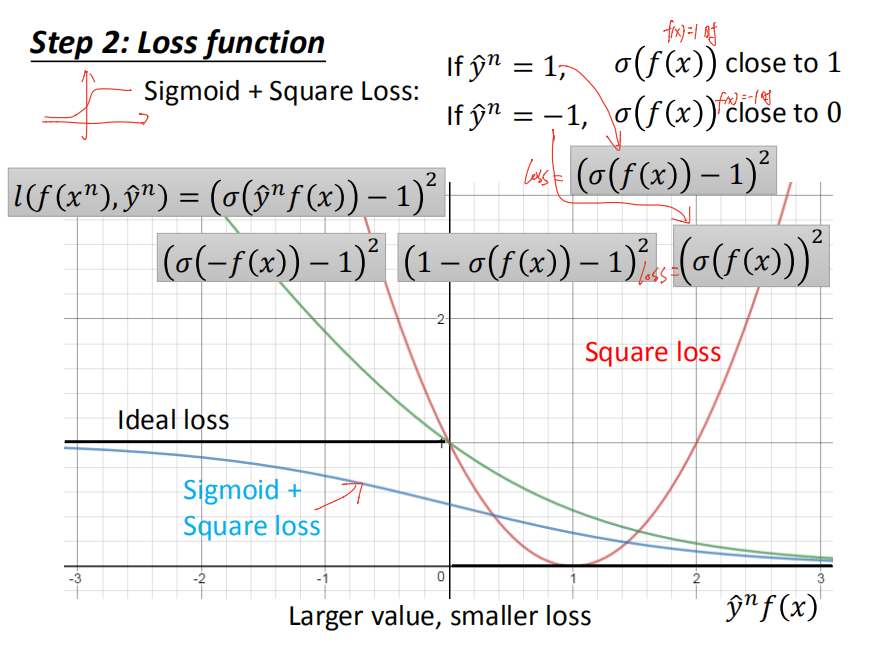
sigmoid+cross entropy

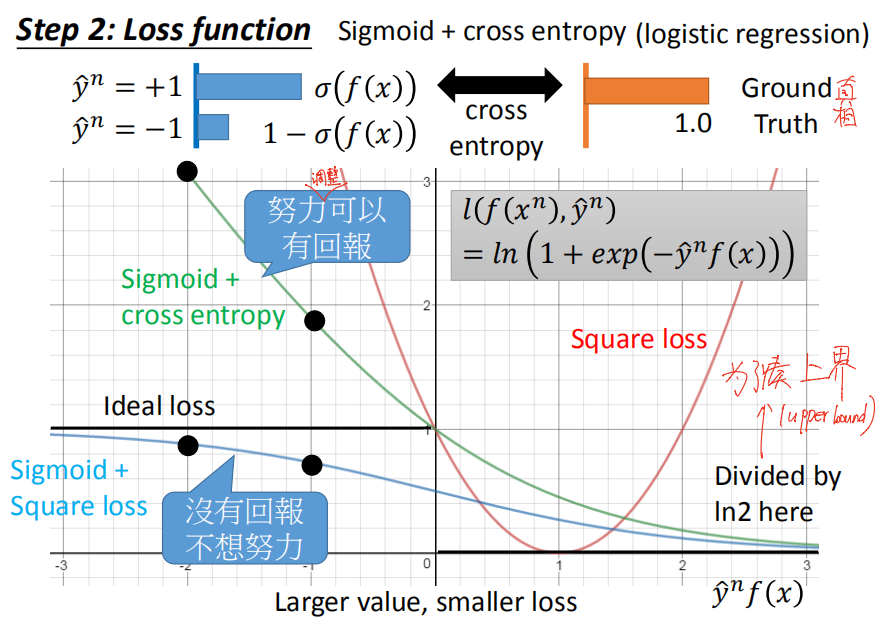
Hinge

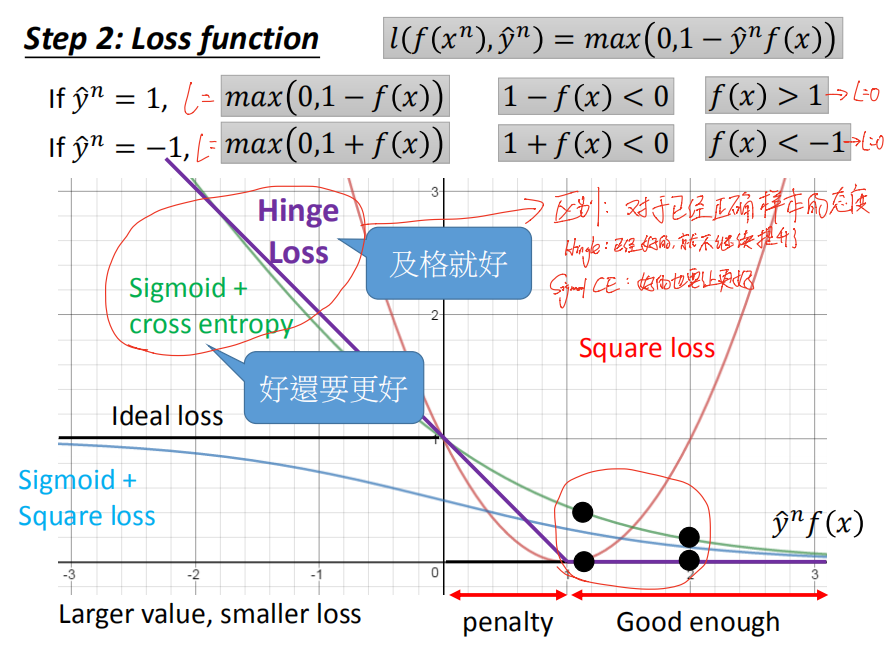
Hinge 与 sigmiod+cross entropy 这两个loss function的区别：对于结果已经正确的样本数据，hinge 就不再继续产生loss用于继续提升，而sigmiod+cross entropy 会继续产生loss 使其再继续远离刚刚能正确分类的点（不满足于刚刚超过阈值）。

2.3

确定好了loss function之后，就可以做梯度下降了。

c(w)有很多都为0，不=0的那些c(w)即为 support vector.
SVM有很好的鲁棒性（robust），因为有很多数据（即那些c(w)=0的）不会影响结果，而 logistic regression 相比就没有这样的鲁棒性。

2.4 Linear SVM的另一种表示形式

3、kernel trick

下面是花书（Deep Learning）中关于SVM的部分，主要就是在说kernel，说的比较宏观比较笼统，先看一下有利于下面深入学习。

3.1

先概括一下我自己理解的kernel trick：利用很多机器学习算法的模型参数都能写成样本间内积的特点，利用核函数代替先转换空间（即非线性ϕ(x)）再内积的方法，来学习非线性模型。

先知道一个事实：w是x的线性组合。
听起来可能难以相信：训练出的模型参数w是数据x的线性组合？解释一下：梯度下降更新参数w时，c(w)只能取0，±1，取0不用说了，取±1时，w就是在±学习率*x

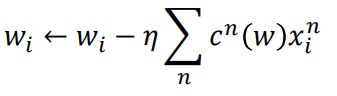
下面看直接看PPT式子就行了。

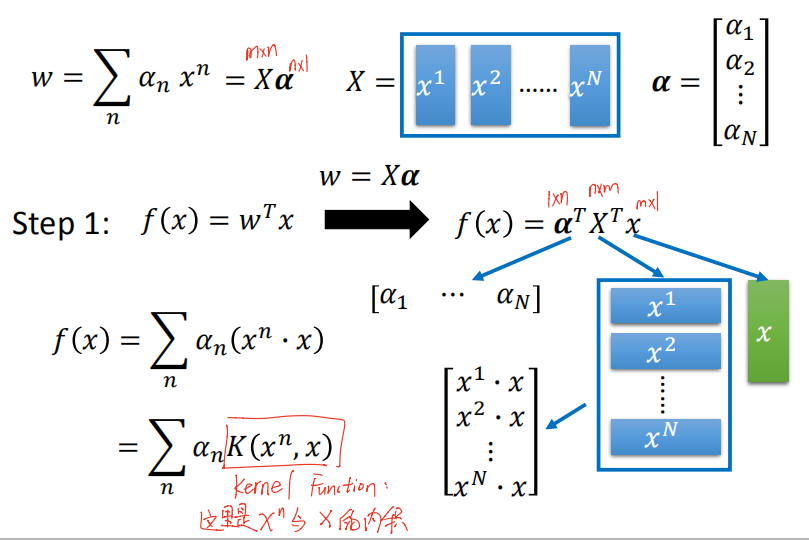
3.2 径向基函数

径向基函数是一个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意一点c的距离，c点称为中心点，也就是Φ（x，c）=Φ(‖x-c‖)。任意一个满足Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数，标准的一般使用欧氏距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。在神经网络结构中，可以作为全连接层和ReLU层的主要函数。

3.3 与神经网络

3.3.1 sigmiod kernel 与神经网络

用sigmiod kernel就相当于一个只有一层hidden layer的神经网络。
每个神经元的参数就是一个输入的data。神经元的个数 ＝ support vector的个数。

3.3.1 SVM 与神经网络

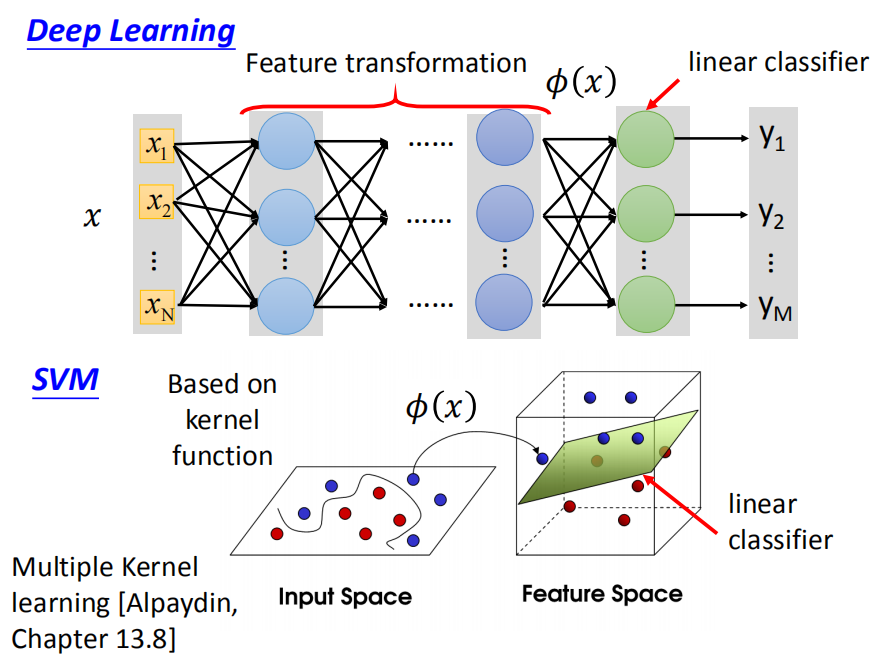
其实kernel是可学习的，但是可学习性没有神经网络参数强，只能给几点kernel然后学习出他们的组合。
只有一个kernel相当于只有一层隐藏层，由多个Kernel组合相当于由多个隐藏层。