st表复习笔记

st表，一种高效的区间最值查询（RMQ）算法。本质其实是一个动态规划。

其实吧，对于看过线性dp的人来说应该不难理解，只是处理有些麻烦。但是本土狗因为-1的问题居然改了许久...

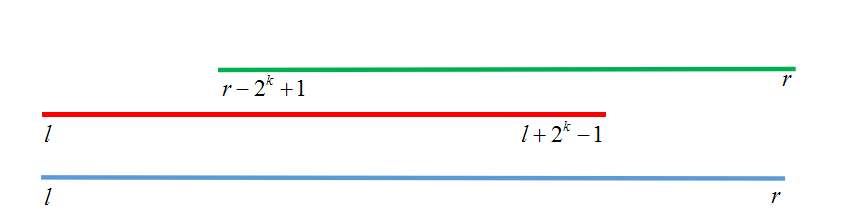
用两个2^i的区间把整个区段覆盖，dp[i][j]表示区间最值，从i开始，向前2^j个数字。根据动态规划的定义，把这个区间分割成两个小区间，于是就有

dp[i][j]=max(dp[i][j-1],dp[i][i+(1<<j-1)]);（然而我在这里处理区间的时候多减了一个1....）

一直分割下去，直到1。复杂度O(nlogn)。

于是查询：

我们找到左右区间大小（y-x+1），把它log一下，再2的次方一下，就成了覆盖区间的最大2^i次方的区间。同理，右区间也是。比较两区间最值，就可以得出最值了。

code：

#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=;
int n,m,a[maxn],dp[maxn][],l[maxn];

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    l[]=-;
    for(int i=;i<=n;++i)
    {
        dp[i][]=a[i];
        l[i]=l[i>>]+;
    }
    for(int j=;j<=;++j)
    {
        for(int i=;i+(<<j)-<=n;++i)
        {
            dp[i][j]=max(dp[i][j-],dp[i+(<<(j-))][j-]);
        }
    }
    for(int i=;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        int s=l[y-x+];
        printf("%d\n",max(dp[x][s],dp[y-(<<s)+][s]));
    }
    return ;
}

类比线段树：

优点：

1、码量小

2、快（不用说了，线段树常数大得呦...）

缺点：

1、只能静态

2、只能最值

（完）