POJ 2155 Matrix （2维树状数组）

POJ-Matrix

题意：给你一个n*n矩阵的灯泡，灯泡的初始状态都为0，T次操作，分别是翻转操作:将x1,y1 --- x2, y2的灯泡状态反转 和 查询操作 找出x1, y1位置灯泡的状态。

题解：开一个2维树状数组进行更新操作。

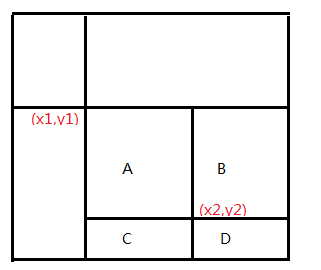
假设我们现在需要翻转A区域内的灯泡， 我们就需要先将ABCD4个区域一起转换，然后再将CB,BD翻转，再将D翻转，这样结束之后就只有A的状态翻转了，所以我们需要先以（x1,y1）为起点更新ABCD区域，再以（x2+1,y1）, (x1,y2+1)对BD, CD进行更新，最后以（x2+1,y2+1）进行更新。

 #include<iostream>
 #include<string>
 #include<cstring>
 using namespace std;
 const int N = +;
 int dp[N][N];
 int n, m;
 int lowbit(int x)
 {
     return x &(-x);
 }
 void Add(int x, int y)
 {
     for(int i = x; i <= n; i += lowbit(i))
         for(int j = y; j <= n; j += lowbit(j))
             dp[i][j]++;
 }
 int Query(int x, int y)
 {
     int cnt = ;
     for(int i = x; i > ; i -= lowbit(i))
         for(int j = y; j > ; j -= lowbit(j))
            cnt += dp[i][j];
     return cnt;
 }
 int main()
 {
     ios::sync_with_stdio(false);
     cin.tie();
     cout.tie();
     int t;
     cin >> t;
     while(t--)
     {
         cin >> n >> m;
         memset(dp, , sizeof(dp));
         string str;
         int x1, y1, x2, y2;
         while(m--)
         {
             cin >> str >> x1 >> y1;
             if(str[] == 'C')
             {
                 cin >> x2 >> y2;
                 Add(x2+,y2+);
                 Add(x1,y1);
                 Add(x1,y2+);
                 Add(x2+,y1);
             }
             else
             {
                 if(Query(x1,y1)&) cout <<  << endl;
                 else cout <<  << endl;
             }
         }
         cout << endl;
     }
     return ;
 }