有关logistic(sigmoid)函数回归

在神经网络中，经常用到sigmoid函数，y = 1 / (1+e^-x)

作为下一级神经元的激活函数，x也就是WX（下文，W以θ符号代替）矩阵计算结果。

这个函数通常用在进行分类，通常分为1或0的逻辑分类，所以又叫logistic回归。

常规常规情况下，我们使用的损失函数是 j(θ) = 1 / 2n * ∑(h_θ(x) - y) ， h_θ(x)  也就是激活函数(或hypothesis函数)，y是样本结果数据。在大部分情况下，这是通用的。以向量来看，空间点H_θ(x)和Y距离最小化。

但是，由于sigmoid函数是非线性的，所以用以上损失函数，求偏导后，得到的 j(θ)只能是局部最小值（左图），得不到真正的最小值。

因此，在logistic回归中，最优的损失函数，应该是：

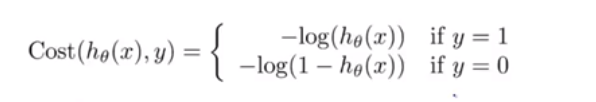
y是指样本值。（也即是损失函数和y的关系，不再是直接减去y(样本目标值)）

图像：

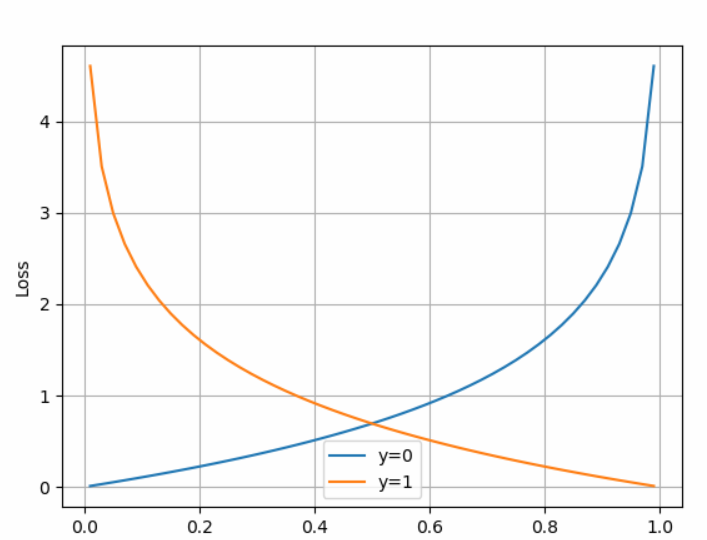
当y=0时，如果H_θ(x)越接近0，那么损失越小。也就是说，只要偏导数为0，反向传播时依然往最小值方向（而非局部最小值）

如果y=0，但是H_θ(x)不接近0，甚至于大于1，那么损失就非常巨大，那么可以造成反响传播时，修改原θ值就越大了。

连个曲线合并，就是J = y * log(x) + (1 - y) * log (1 - x)，y的取值只能为0或1

整个损失函数简化后，得到：

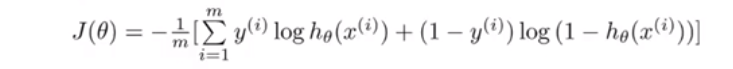（此函数，又叫交叉熵函数）

θ其实也即是权，或参数值。

总的来说，根据学习的结果类型（是0或1类型，还是数值类型），选择合适的激活函数，同时，也要有对应的损失函数，才能得到最佳效果。