二叉树根结点到任意结点的路径（C语言）

有一棵二叉树，如下图所示：

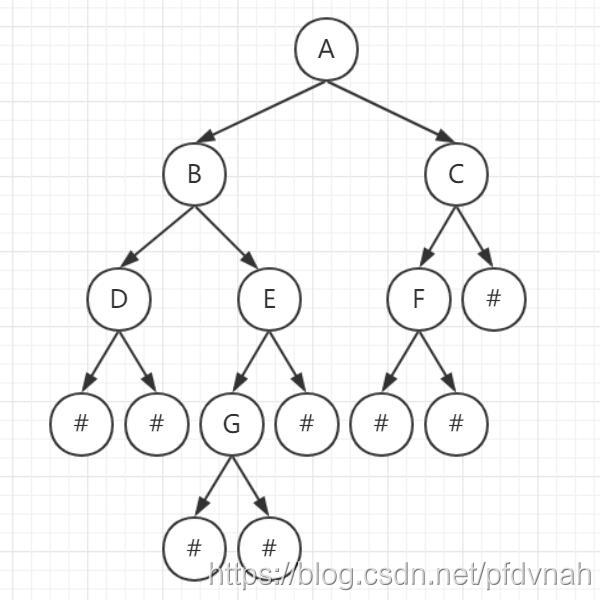
其中 # 表示空结点。

先序遍历：A B D E G C F

问题：怎么得到从根结点到任意结点的路径呢？

示例：输入 G，怎么得到从结点 A 到结点 G 的路径呢？

很明显，我们一眼就能看出来路径是 A B E G。如何通过程序得到这条路径就是我们接下来需要做的。

定义二叉树的 链式存储结构 如下：

typedef struct BiTNode {
	char data;
	struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;// 二叉树结点的存储结构

二叉树的遍历有三种方式：即先序遍历，中序遍历，后序遍历。

先序遍历是先访问结点再递归子树。我们只需要访问到目标结点的时候就知道了路径就可以结束递归，因此正好符合要求。另外两个也可以得到路径，但是还要先访问子树，显然是没必要的。

先序遍历可以通过递归实现，我们只需要加个容器来保存路径即可。栈 正好满足要求。由于不知道路径的长度，因此采用 链栈 来实现。

链栈 结构如下：

typedef struct StackNode {
	char data;
	struct StackNode* next;
}StackNode, * Stack;// 链栈

完整代码：

/*************************************************************************
	实现功能：	输出从根结点到指定结点的路径
	编译环境：	Visual Studio 2019
	更新日期：	2019年10月10日15:16:28
	更新内容：	增加清空二叉树和栈的函数
				优化if判断条件
	博客链接：	https://blog.csdn.net/pfdvnah/article/details/102387839
	作者：		wowpH
*************************************************************************/

#define _CRT_SECURE_NO_WARNINGS

#include<stdio.h>
#include<stdlib.h>// exit,malloc,free头文件

#define EMPTY_NODE '#'
#define TRUE 1
#define FALSE 0
#define STACK_EMPTY TRUE
#define STACK_NOT_EMPTY FALSE
#define FOUND TRUE
#define NOT_FOUND FALSE

typedef struct BiTNode {
	char data;
	struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;// 二叉链表

typedef struct StackNode {
	char data;
	struct StackNode* next;
}StackNode, * Stack;// 链栈

// 创建二叉树结点，返回创建的二叉树结点
BiTree createBiTNode();
// 创建二叉树，返回根结点
BiTree createBiTree();
// 初始化二叉树，返回根结点
BiTree initBiTree();
// 清空二叉树
void clearBiTree(BiTree T);

// 创建栈结点，返回创建的栈结点
Stack createStackNode();
// 初始化栈，返回栈的头结点
Stack initStack();
// 栈是否初始化
int isStackExist(Stack S);
// 栈是否为空
int isStackEmpty(Stack S);
// 入栈
char push(Stack S, char data);
// 出栈
char pop(Stack S);
// 查看栈顶元素
char peek(Stack S);
// 清空栈
void clearStack(Stack S);

// 寻找路径，返回是否找到目标结点
int searchPath(BiTree T, Stack S);
// 是否找到目标结点
int isFindTargetNode(Stack S);
// 显示路径
void showPath(Stack S);
// 输出路径
void outputPath(Stack S);

// 输出程序提示信息
void outputTips();

int main() {
	outputTips();// 输出程序提示信息
	BiTree tree = initBiTree();
	Stack stack = initStack();// 头结点存储目标结点信息
	searchPath(tree, stack);// 寻找路径
	showPath(stack);// 输出路径信息
	clearBiTree(tree);// 清空二叉树
	clearStack(stack);// 清空栈
	return 0;
}

/******************************** 二叉树 ********************************/
// 创建二叉树结点
BiTree createBiTNode() {
	BiTree newNode = (BiTree)malloc(sizeof(BiTNode));
	if (newNode == NULL) {
		printf("错误（%d）：创建二叉树结点错误！\n", __LINE__);
		exit(0);
	}
	newNode->lchild = NULL;
	newNode->rchild = NULL;
	return newNode;
}

// 创建二叉树
BiTree createBiTree() {
	char ch = getchar();
	if (ch != '\n' && ch != EMPTY_NODE) {
		BiTree T = createBiTNode();
		T->data = ch;
		T->lchild = createBiTree();// 左子树
		T->rchild = createBiTree();// 右子树
		return T;
	}
	return NULL;
}

// 初始化二叉树
BiTree initBiTree() {
	printf("输入二叉树：");
	BiTree tree = createBiTree();
	char enter = getchar();
	return tree;
}

// 清空二叉树
void clearBiTree(BiTree T) {
	if (T != NULL) {
		clearBiTree(T->lchild);
		clearBiTree(T->rchild);
		free(T);
	}
}

/********************************** 栈 **********************************/
// 创建栈结点
Stack createStackNode() {
	Stack newNode = (Stack)malloc(sizeof(StackNode));
	if (newNode == NULL) {
		printf("错误（%d）：创建栈结点错误！\n", __LINE__);
		exit(0);
	}
	newNode->next = NULL;
	return newNode;
}

// 初始化栈，并返回头结点
Stack initStack() {
	printf("输入指定结点：");
	char targetNode = getchar();
	Stack stack = createStackNode();// 头结点存储目标结点数据
	stack->data = targetNode;
	return stack;
}

// 栈头结点是否存在
int isStackExist(Stack S) {
	if (S == NULL) {
		printf("错误（%d）：栈的头结点未初始化！\n", __LINE__);
		exit(0);
	}
	return TRUE;
}

// 栈是否为空
int isStackEmpty(Stack S) {
	if (isStackExist(S) == FALSE) {
		return STACK_EMPTY;
	}
	if (S->next == NULL) {
		return STACK_EMPTY;
	}
	return STACK_NOT_EMPTY;
}

// 入栈，data是要入栈的结点的数据
char push(Stack S, char data) {
	if (isStackExist(S) == TRUE) {
		Stack node = createStackNode();
		node->data = data;
		node->next = S->next;
		S->next = node;
	}
	return data;
}

// 出栈，返回栈顶结点的数据
char pop(Stack S) {
	char ret = STACK_EMPTY;
	if (isStackEmpty(S) == STACK_NOT_EMPTY) {
		Stack delete = S->next;
		S->next = delete->next;
		ret = delete->data;
		free(delete);
	}
	return ret;
}

// 查看栈顶元素
char peek(Stack S) {
	return isStackEmpty(S) == STACK_EMPTY ? STACK_EMPTY : S->next->data;
}

// 清空栈
void clearStack(Stack S) {
	while (isStackEmpty(S) == STACK_NOT_EMPTY) {
		pop(S);
	}
	free(S);
}

/********************************* 路径 *********************************/
// 寻找路径
int searchPath(BiTree T, Stack S) {
	if (isFindTargetNode(S) == FOUND) {
		return FOUND;
	}
	if (T == NULL) {// 空树
		return NOT_FOUND;
	}
	push(S, T->data);
	// 查找子树
	if (searchPath(T->lchild, S) == FOUND) {
		return FOUND;
	}
	if (searchPath(T->rchild, S) == FOUND) {
		return FOUND;
	}
	pop(S);
	return NOT_FOUND;
}

// 是否找到目标结点
int isFindTargetNode(Stack S) {
	if (isStackEmpty(S) == STACK_NOT_EMPTY && peek(S) == S->data) {
		return FOUND;
	}
	return NOT_FOUND;
}

// 输出路径，递归
void outputPath(Stack S) {
	if (isStackEmpty(S) == STACK_NOT_EMPTY) {
		outputPath(S->next);
		if (isStackEmpty(S->next) == STACK_NOT_EMPTY) {
			printf(" ");
		}
		printf("%c", S->next->data);
	}
}

// 显示路径
void showPath(Stack S) {
	if (isFindTargetNode(S) == FOUND) {
		printf("路径：");
		outputPath(S);
		printf("\n");
	} else {
		printf("未找到结点'%c'\n", S->data);
	}
}

// 输出提示
void outputTips() {
	printf("1、先序输入二叉树\n");
	printf("2、空结点用'%c'表示\n", EMPTY_NODE);
	printf("3、Enter表示输入结束\n");
	printf("4、字符个数必须正确\n");
}

/*************************************************************************
1、先序输入二叉树
2、空结点用'#'表示
3、Enter表示输入结束
4、字符个数必须正确

示例1：
输入二叉树：ABD##EG###CF###
输入指定结点：G
路径：A B E G

示例2：
输入二叉树：124##56##7##3##
输入指定结点：7
路径：1 2 5 7
*************************************************************************/