【微信小程序】 小程序中的递归运算/二分查找算法/Maximum call stack size exceeded

摘要： 小程序中的递归运算/二分查找算法/Maximum call stack size exceeded

场景：最近做一个车贷计算器， 其中存在一个公式如下：

　

    /****
    总金额 * 月利率 * (1+月利率)^贷款期限 / ( (1+月利率)^贷款期限 — 1) = 月还款额
    totalmoney --- 总金额
    month_rate --- 月利率
    year_rate ----  月利率*12 --- month_rate*12
    limit --- 贷款期限
    monthsup --- 月还款额
    共有4个变量totalmoney, month_rate, limit, monthsup
    在知道totalmoney, month_rate, limit时计算monthsup是简单的, 但是由其他三个倒推出 monthsup 呢？
    ****/

利用数学方法解决这个问题可太难了，我在微博求助@毕导THU，毕导竟然给我解出来了。。。这清华的博士真是吓到我了。。

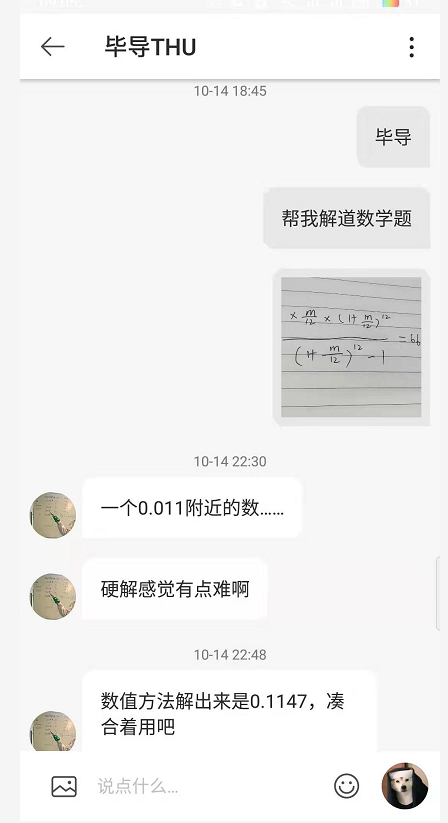
这里我们来想想怎么用代码来算出年利率/ 月利率

已知利率是0到1之间的数，大于0小于1

思路： 递归思想， 二分查找算法，

代码：

    function myfn(min, max, totalmoney, limit, monthsup){
      let month_rate = (min + max)/2
      let num = totalmoney * month_rate * Math.pow((1+month_rate),limit) / (Math.pow((1+month_rate),limit) - 1)
      if(parseFloat(num.toFixed(2)) == parseFloat(monthsup.toFixed(2))) {
        let monthRate = (Math.round(month_rate*10000)/100).toFixed(2)
        let year_rate = 12 * month_rate
        year_rate = (Math.round(year_rate*10000)/100).toFixed(2)
        return [year_rate, monthRate]
      }else if(parseFloat(num.toFixed(2)) > parseFloat(monthsup.toFixed(2))) {
        max = (min + max)/2
        return myfn(min, max, totalmoney, limit, monthsup)
      }else if(parseFloat(num.toFixed(2)) < parseFloat(monthsup.toFixed(2))) {
        min = (min + max)/2
        return myfn(min, max, totalmoney, limit, monthsup)
      }
    }

注释： 这里其实就是一个递归的应用， 我们先取0和1的平均值， 带入公式中，将得到的值num与已知的月还款额进行比较， 若大于月还款额， 此时我们得到了一个更精确的范围， 即 月利率 的最大值为 0和1 的平均值， 然后_max = （min + max）/ 2，max =_max 再调用我们的函数myfn， 再次运算， 若num小于月还款额， 我们也能得到一个更精确的范围， 即 月利率的最小值为 0和 _max 的平均值， 。。。。这样直到已知的月还款额等于num， return 出年利率 / 月利率

重点提示： 细心的你可能已经发现了， 上面代码有许多的toFixed， 这不仅仅是根据产品需求所做的一个数据处理， 也是我们一定要做的一个限制，

如果不做这个限制的话， 递归函数将会进行巨量的计算，  直到num无限接近已知的月还款额， 但是我们并不需要得到这么精确的数据，只需要精确到小数点后两位或者三位， 四位即可，

（不加限制的时候，会出现这个错误， Maximum call stack size exceeded ，百度结果是 “超过最大调用堆栈大小”）

将代码搬到小程序上：

    myfn (min, max, totalmoney, limit, monthsup) {
        totalmoney = parseFloat(totalmoney)
        monthsup = parseFloat(monthsup)
        let month_rate = (min + max)/2
        let num = totalmoney * month_rate * Math.pow((1+month_rate),limit) / (Math.pow((1+month_rate),limit) - 1)
        if(parseFloat(num.toFixed(2)) == parseFloat(monthsup.toFixed(2))) {
            let monthRate = (Math.round(month_rate*10000)/100).toFixed(2)
            let year_rate = 12 * month_rate
            year_rate = (Math.round(year_rate*10000)/100).toFixed(2)
            return [monthRate, year_rate]
        }else if(parseFloat(num.toFixed(2)) > parseFloat(monthsup.toFixed(2))) {
            max = (min + max)/2
            return this.myfn(min, max, totalmoney, limit, monthsup) //************ return this.fn
        }else if(parseFloat(num.toFixed(2)) < parseFloat(monthsup.toFixed(2))) {
            min = (min + max)/2
            return this.myfn(min, max, totalmoney, limit, monthsup)// ************* return this.fn

} },

在将代码搬到小程序时一定要注意， 递归函数内不符合条件时return fn 要改成 retrun this.fn ， 否则 函数在进行完第一轮就不会再运行了， 因为它找不到fn， 我找个错误找了很久。。。。

就这吧， 新bug来了， 接着改bug。。。。