RMQ问题（超详细！！！）

一、简介

RMQ是询问某个区间内的最大值或最小值，暴力解法对每个询问区间用循环找最值，当n、q>10000会TLE。

常用RMQ的求解方法——ST算法。

ST算法通常用在要多次询问一些区间的最值的问题中。它可以做到O(nlogn)的预处理，O(1)回答每个询问。

使用ST算法的条件是无修改，因此它适用于没有修改并且询问次数较多（10^6级别甚至更大）的情况。

优点：代码短，效率高，实现简单

缺点：适用性差

二、ST算法流程

预处理:

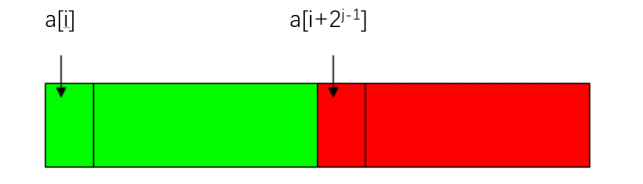
ST算法的原理实际上是动态规划，我们用a[1...n]表示一组数。设f[i, j]表示从a[i]到a[i + 2j - 1]这个范围内的最大值，也就是以a[i]为起点连续2j个数的最大值。由于元素个数为2j个，所以从中间平均分成两部分，每一部分的元素个数刚好为2j-1个，也就是说，把f[i,j]分为f[i, j-1]和f[i + 2j-1, j-1]，如下图：

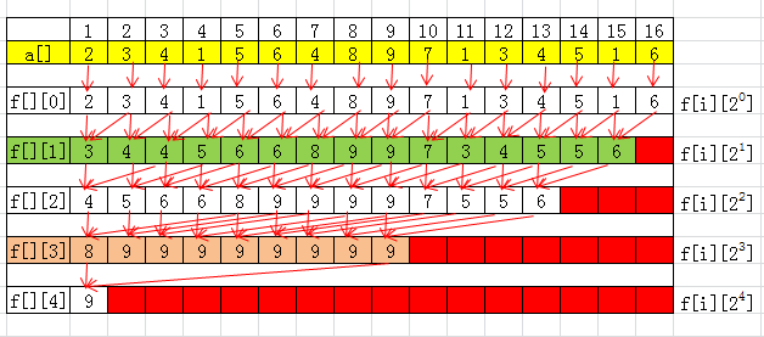
举个栗子吧——如下图所示

整个区间的最大值一定是左右两部分最大值的较大值，满足动态规划的最优化原理，分析得到状态转移方程：

f[i][j] = max(f[i][j - 1], f[i + 2j-1][j - 1])，边界条件为f[i][0] = a[i]，这样就可以在O(nlogn)的时间复杂度内预处理f数组。

for(int j=;j<=LN;j++)

　　for(int i=;i+(<<j)-<=n;i++)

　　　　f[i][j]=max(f[i][j-],f[i+(<<(j-))][j-]); // <<左移运算符，优化时间常数

询问

若我们要询问区间[li, ri]的最大值，则先求出最大的x满足2x（此处为2的x次方）≤ ri - li + 1，推出x=log2(ri-li+1)

那么区间[li, ri]=[li, li+2x-1]U[ri-2x+1, ri] ，如下图所示：

ans = max(f[li][x], f[ri–2x +1][x])；

两个区间的元素个数都为2x，所以[li, ri]的最大值为max(f[li][x], f[ri - 2x + 1][x])，可以在O(1)内计算出来。虽然这两个区间有交集，但是对于求区间最值来说没有影响，这就是ST算法只适用于求区间最值的原因。

技巧:

因为cmath库中的log2函数效率不高，所以除了调用log2函数外，通常还会使用O(N)递推预处理出1~N这N种区间长度各自对应的k值。具体地，设lg[d]表示log2d下取整，log2d=log2((d/2)*2)=log2(d/2) + 1则lg[d] = lg[d/2]+1。

lg[]=-;//为了lg[1]=0;
for(int i=;i<=n;i++)
    lg[i]=lg[i>>]+;// >> 右移运算符，优化时间常数

那么再来看一道例题吧——

1541：【例 1】数列区间最大值

【题目描述】

输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

【输入】

第一行两个整数 N,M 表示数字的个数和要询问的次数； 接下来一行为 N个数； 接下来 M行，每行都有两个整数 X,Y。

【输出】

输出共 M行，每行输出一个数。

【输入样例】

10 2

3 2 4 5 6 8 1 2 9 7

1 4

3 8

【输出样例】

5

8

---