Java八大排序之插入排序

插入排序

也可叫直接插入排序，该算法的思路是：初始可认为文件中的第1个记录已排好序，然后将第2个到第n个记录依次插入到已排序的记录组成的文件中。

步骤：

假设有一组数组为（数组下标0—n-1）：

arrays={49,38,65,97,176,213,227,49,78,34,12,164,11,18,1};

一，从下标为1的数据（当前数据）开始遍历，而且之后往后移直到下标为n-1（数组的最后一位下标数据）；
二，定义一个变量并保存当前数据；
三，当前数据与前面数据依次对比直到前面数据的下标为0，如果大于当前数据，则把前面的数据往右移一位；
四，每执行第三步后，将之前保存当前数据的变量赋值为给前面数据的下标加1.

流程图：

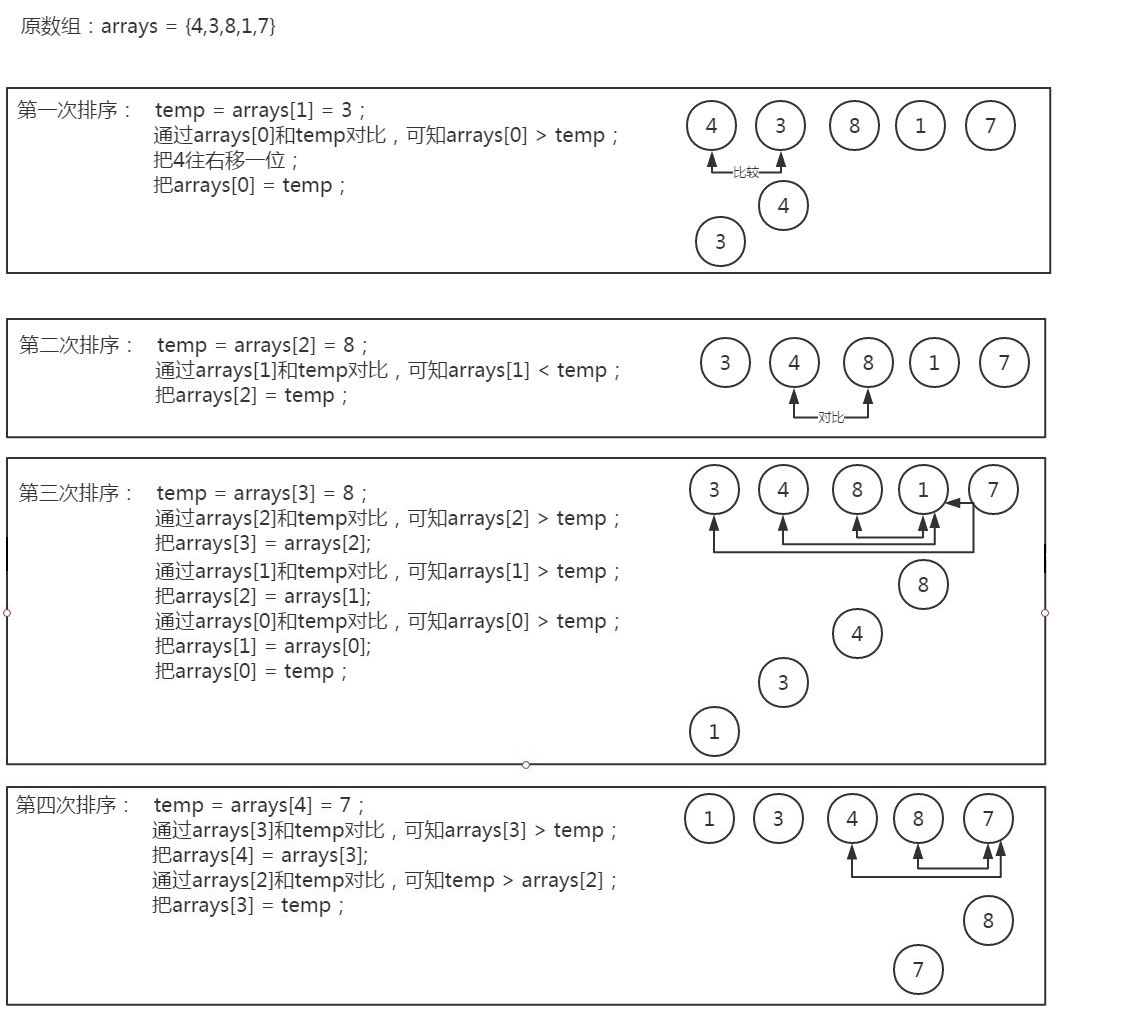
代码：

 public class TestInsert {
     //直接插入排序
     public static void insertSort(int[] arrays){
         int i,j;
         //从第二位开始遍历，（之后把第i位数据叫作当前数据）
         for (i = 1; i <arrays.length; i++){
             //保存当前数据为temp
             int temp = arrays[i];
             j = i - 1;  //把 j 赋值为 i 的前一个数据
             //循环，如果j大于等于0 且 第j个数据大于当前数据
             while (j >= 0 && arrays[j] > temp){
                 arrays[j+1] = arrays[j];    //第j个数据往右移一位
                 j = j - 1;      //往前一位一位移动
             }
             //把当前数据赋给arrays[j+1],因为在while循环内最后总会j-1
             arrays[j+1] = temp;
             System.out.println("第"+i+"次："+Arrays.toString(arrays));
         }
         System.out.println("最后结果："+Arrays.toString(arrays));
     }

     public static void main(String[] args) {
         int[] arrays={49,38,65,97,176,213,227,49,78,34,12,164,11,18,1};
         insertSort(arrays);
     }
 }

测试结果：

第1次：[38, 49, 65, 97, 176, 213, 227, 49, 78, 34, 12, 164, 11, 18, 1]
第2次：[38, 49, 65, 97, 176, 213, 227, 49, 78, 34, 12, 164, 11, 18, 1]
第3次：[38, 49, 65, 97, 176, 213, 227, 49, 78, 34, 12, 164, 11, 18, 1]
第4次：[38, 49, 65, 97, 176, 213, 227, 49, 78, 34, 12, 164, 11, 18, 1]
第5次：[38, 49, 65, 97, 176, 213, 227, 49, 78, 34, 12, 164, 11, 18, 1]
第6次：[38, 49, 65, 97, 176, 213, 227, 49, 78, 34, 12, 164, 11, 18, 1]
第7次：[38, 49, 49, 65, 97, 176, 213, 227, 78, 34, 12, 164, 11, 18, 1]
第8次：[38, 49, 49, 65, 78, 97, 176, 213, 227, 34, 12, 164, 11, 18, 1]
第9次：[34, 38, 49, 49, 65, 78, 97, 176, 213, 227, 12, 164, 11, 18, 1]
第10次：[12, 34, 38, 49, 49, 65, 78, 97, 176, 213, 227, 164, 11, 18, 1]
第11次：[12, 34, 38, 49, 49, 65, 78, 97, 164, 176, 213, 227, 11, 18, 1]
第12次：[11, 12, 34, 38, 49, 49, 65, 78, 97, 164, 176, 213, 227, 18, 1]
第13次：[11, 12, 18, 34, 38, 49, 49, 65, 78, 97, 164, 176, 213, 227, 1]
第14次：[1, 11, 12, 18, 34, 38, 49, 49, 65, 78, 97, 164, 176, 213, 227]
最后结果：[1, 11, 12, 18, 34, 38, 49, 49, 65, 78, 97, 164, 176, 213, 227]

时间复杂度：因为外层循环为n-1，所以在最好的情况下，序列本身就是有序的，那么时间复杂度为O(n)；最坏的情况下循环次数为n*（n-1）/2，那么时间复杂度为O(n²)。

空间复杂度：插入排序算法，只需要两个变量暂存当前数，以及下标，与n的大小无关，所以空间复杂度为：O(1)。

结语：

　　语言表达能力不好，所以只能这样了，还有就是应该还有这个算法的优缺点没有写，明着说，我还不知道。