[LeetCode] 723. Candy Crush 糖果粉碎

This question is about implementing a basic elimination algorithm for Candy Crush.

Given a 2D integer array board representing the grid of candy, different positive integers board[i][j] represent different types of candies. A value of board[i][j] = 0 represents that the cell at position (i, j) is empty. The given board represents the state of the game following the player's move. Now, you need to restore the board to a stable state by crushing candies according to the following rules:

1. If three or more candies of the same type are adjacent vertically or horizontally, "crush" them all at the same time - these positions become empty.
2. After crushing all candies simultaneously, if an empty space on the board has candies on top of itself, then these candies will drop until they hit a candy or bottom at the same time. (No new candies will drop outside the top boundary.)
3. After the above steps, there may exist more candies that can be crushed. If so, you need to repeat the above steps.
4. If there does not exist more candies that can be crushed (ie. the board is stable), then return the current board.

You need to perform the above rules until the board becomes stable, then return the current board.

Example 1:

Input:
board =
[[110,5,112,113,114],[210,211,5,213,214],[310,311,3,313,314],[410,411,412,5,414],[5,1,512,3,3],[610,4,1,613,614],[710,1,2,713,714],[810,1,2,1,1],[1,1,2,2,2],[4,1,4,4,1014]]
Output:
[[0,0,0,0,0],[0,0,0,0,0],[0,0,0,0,0],[110,0,0,0,114],[210,0,0,0,214],[310,0,0,113,314],[410,0,0,213,414],[610,211,112,313,614],[710,311,412,613,714],[810,411,512,713,1014]]
Explanation:

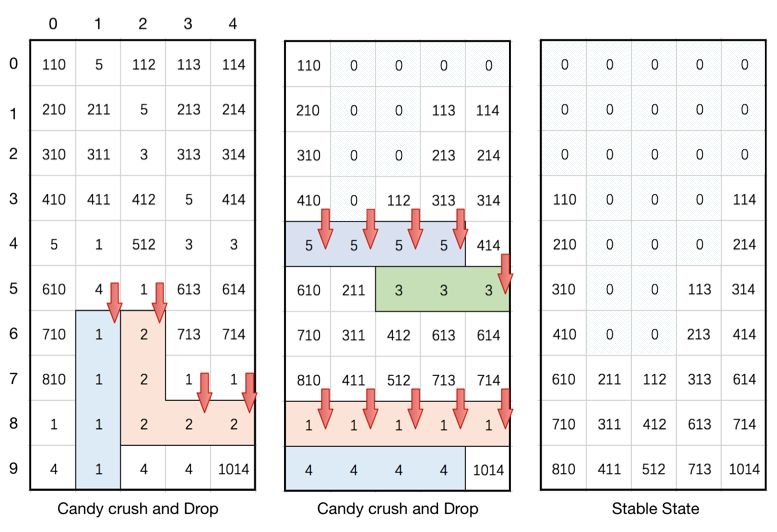
Note:

1. The length of board will be in the range [3, 50].
2. The length of board[i] will be in the range [3, 50].
3. Each board[i][j] will initially start as an integer in the range [1, 2000].

一个类似糖果消消乐游戏的题，给一个二维数组board，数组代表糖果，在水平和竖直方向上3个或以上连续相同的数字可以被消除，消除后位于上方的数字会填充空位。注意是所以能消除的糖果消除后然后再落下，进行第二次消除。直到最后没有能消除的了，达到稳定状态。

解法：标记出所有需要被crush的元素，然后去掉这些元素，将上面的数下降，空位变为0。难的地方是如何确定哪些元素需要被crush。

Python:

class Solution(object):
    def candyCrush(self, board):
        """
        :type board: List[List[int]]
        :rtype: List[List[int]]
        """
        R, C = len(board), len(board[0])
        changed = True

        while changed:
            changed = False

            for r in xrange(R):
                for c in xrange(C-2):
                    if abs(board[r][c]) == abs(board[r][c+1]) == abs(board[r][c+2]) != 0:
                        board[r][c] = board[r][c+1] = board[r][c+2] = -abs(board[r][c])
                        changed = True

            for r in xrange(R-2):
                for c in xrange(C):
                    if abs(board[r][c]) == abs(board[r+1][c]) == abs(board[r+2][c]) != 0:
                        board[r][c] = board[r+1][c] = board[r+2][c] = -abs(board[r][c])
                        changed = True

            for c in xrange(C):
                i = R-1
                for r in reversed(xrange(R)):
                    if board[r][c] > 0:
                        board[i][c] = board[r][c]
                        i -= 1
                for r in reversed(xrange(i+1)):
                    board[r][c] = 0

        return board　

C++:

// Time:  O((R * C)^2)
// Space: O(1)

class Solution {
public:
    vector<vector<int>> candyCrush(vector<vector<int>>& board) {
        const auto R = board.size(), C = board[0].size();
        bool changed = true;

        while (changed) {
            changed = false;

            for (int r = 0; r < R; ++r) {
                for (int c = 0; c + 2 < C; ++c) {
                    auto v = abs(board[r][c]);
                    if (v != 0 && v == abs(board[r][c + 1]) && v == abs(board[r][c + 2])) {
                        board[r][c] = board[r][c + 1] = board[r][c + 2] = -v;
                        changed = true;
                    }
                }
            }

            for (int r = 0; r + 2 < R; ++r) {
                for (int c = 0; c < C; ++c) {
                    auto v = abs(board[r][c]);
                    if (v != 0 && v == abs(board[r + 1][c]) && v == abs(board[r + 2][c])) {
                        board[r][c] = board[r + 1][c] = board[r + 2][c] = -v;
                        changed = true;
                    }
                }
            }

            for (int c = 0; c < C; ++c) {
                int empty_r = R - 1;
                for (int r = R - 1; r >= 0; --r) {
                    if (board[r][c] > 0) {
                        board[empty_r--][c] = board[r][c];
                    }
                }
                for (int r = empty_r; r >= 0; --r) {
                    board[r][c] = 0;
                }
            }
        }

        return board;
    }
};　　

C++:

class Solution {
public:
    vector<vector<int>> candyCrush(vector<vector<int>>& board) {
        int m = board.size(), n = board[0].size();
        while (true) {
            vector<pair<int, int>> del;
            for (int i = 0; i < m; ++i) {
                for (int j = 0; j < n; ++j) {
                    if (board[i][j] == 0) continue;
                    int x0 = i, x1 = i, y0 = j, y1 = j;
                    while (x0 >= 0 && x0 > i - 3 && board[x0][j] == board[i][j]) --x0;
                    while (x1 < m && x1 < i + 3 && board[x1][j] == board[i][j]) ++x1;
                    while (y0 >= 0 && y0 > j - 3 && board[i][y0] == board[i][j]) --y0;
                    while (y1 < n && y1 < j + 3 && board[i][y1] == board[i][j]) ++y1;
                    if (x1 - x0 > 3 || y1 - y0 > 3) del.push_back({i, j});
                }
            }
            if (del.empty()) break;
            for (auto a : del) board[a.first][a.second] = 0;
            for (int j = 0; j < n; ++j) {
                int t = m - 1;
                for (int i = m - 1; i >= 0; --i) {
                    if (board[i][j]) swap(board[t--][j], board[i][j]);
                }
            }
        }
        return board;
    }
};

C++:

class Solution {
public:
    vector<vector<int>> candyCrush(vector<vector<int>>& board) {
        int m = board.size(), n = board[0].size();
        bool toBeContinued = false;

        for (int i = 0; i < m; ++i) { // horizontal crushing
            for (int j = 0; j + 2 < n; ++j) {
                int& v1 = board[i][j];
                int& v2 = board[i][j+1];
                int& v3 = board[i][j+2];

                int v0 = std::abs(v1);

                if (v0 && v0 == std::abs(v2) && v0 == std::abs(v3)) {
                    v1 = v2 = v3 = - v0;
                    toBeContinued =  true;
                }
            }
        }

        for (int i = 0; i + 2 < m; ++i) {  // vertical crushing
            for (int j = 0; j < n; ++j) {
                int& v1 = board[i][j];
                int& v2 = board[i+1][j];
                int& v3 = board[i+2][j];
                int v0 = std::abs(v1);
                if (v0 && v0 == std::abs(v2) && v0 == std::abs(v3)) {
                    v1 = v2 = v3 = -v0;
                    toBeContinued = true;
                }
            }
        }

        for (int j = 0; j < n; ++j) { // gravity step
            int dropTo = m - 1;
            for (int i = m - 1; i >= 0; --i) {
                if (board[i][j] >= 0) {
                    board[dropTo--][j] = board[i][j];
                }
            }

            for (int i = dropTo; i >= 0; i--) {
                board[i][j] = 0;
            }
        }

        return toBeContinued ? candyCrush(board) : board;

    }
};

　　

　　

All LeetCode Questions List 题目汇总