FFT用到的各种素数

int MOD;
inline int mul(int a, int b){
    return (long long)a * b % MOD;
}
int power(int a, int b){
    int ret = ;
    for (int t = a; b; b >>= ){
        if (b & )ret = mul(ret, t);
        t = mul(t, t);
    }
    return ret;
}
int cal_root(int mod)
{
    int factor[], num = , s = mod - ;
    MOD = mod--;
    for (int i = ; i * i <= s; i++){
        if (s % i == ){
            factor[num++] = i;
            while (s % i == )s /= i;
        }
    }
    if (s != )factor[num++] = s;
    for (int i = ;; i++){
        int j = ;
        for (; j < num && power(i, mod / factor[j]) != ; j++);
        if (j == num)return i;
    }
}

有用的表格

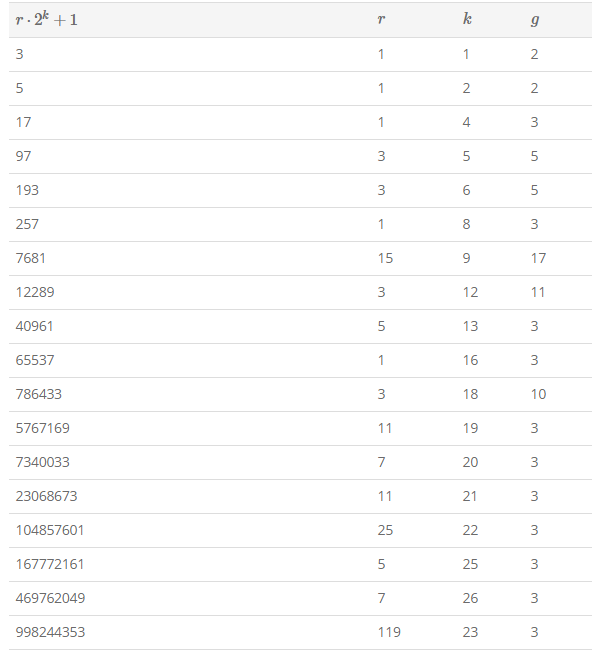
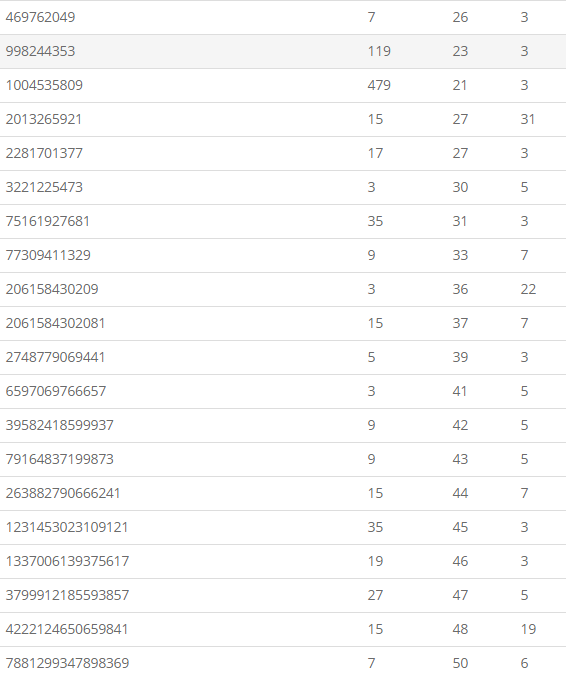
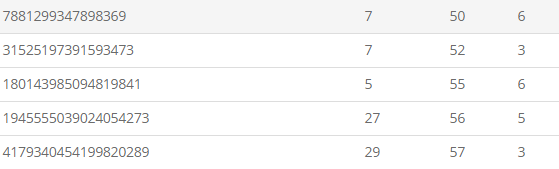
详细 http://blog.miskcoo.com/2014/07/fft-prime-table