HDU4188：RealPhobia （连分数的运用之一）

Bert is a programmer with a real fear of floating point arithmetic. Bert has quite successfully used rational numbers to write his programs but he does not like it when the denominator grows large. Your task is to help Bert by writing a program that decreases the denominator of a rational number, whilst introducing the smallest error possible. For a rational number A/B, where B > 2 and 0 < A < B, your program needs to identify a rational number C/D such that: 
1. 0 < C < D < B, and 
2. the error |A/B - C/D| is the minimum over all possible values of C and D, and 
3. D is the smallest such positive integer.

InputThe input starts with an integer K (1 <= K <= 1000) that represents the number of cases on a line by itself. Each of the following K lines describes one of the cases and consists of a fraction formatted as two integers, A and B, separated by “/” such that: 
1. B is a 32 bit integer strictly greater than 2, and 
2. 0 < A < BOutputFor each case, the output consists of a fraction on a line by itself. The fraction should be formatted as two integers separated by “/”.Sample Input

3
1/4
2/3
13/21

Sample Output

1/3
1/2
8/13

题意：给定分数A/B，求C/D（满足D<B），使得C/D最接近A/B。

思路：可以用扩展欧几里德解决。这里是新认识了一种利用“连分数”来解决的做法。

连分数将A/B表示为一连续的分数=1/（B/A+B%A），然后B%A又继续递推，直到A=1，这时令B=B-1，然后带回这个连分数，就可以得到最接近的分数。

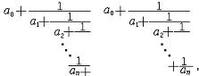
（如果是令B=B+1，得到的分数更接近A/B，但是不满足D<B。

（连分数还可以求把X开根号表示为分数。

#include<bits/stdc++.h>
using namespace std;
int a[],num;
void solve(int x,int y)
{
    num=; int t;
    while(x!=){
        a[++num]=y/x;
        t=x; x=y%x; y=t;
    }
    int C=,D=y-;
    while(num>=){
        t=D;D=a[num]*D+C;C=t;
        num--;
    }
    printf("%d/%d\n",C,D);
}
int main()
{
    int T,A,B,i,j;
    scanf("%d",&T);
    while(T--){
        scanf("%d/%d",&A,&B);
        int g=__gcd(A,B);
        if(A==) printf("%d/%d\n",A,B-);
        else if(g>) printf("%d/%d\n",A/g,B/g);
        else solve(A,B);
    }
    return ;
}