[HAOI2011]Problem b 题解
题目大意:
对于给出的n个询问,每次求有多少个数对(x,y),满足a≤x≤b,c≤y≤d,且gcd(x,y)=k。
思路:
设f(k)为当1≤x≤n,1≤y≤m,且n≤m,使gcd(x,y)=k的数对(x,y)的对数,g(k)为当1≤x≤n,1≤y≤m,且n≤m,使k|gcd(x,y)的数对(x,y)的对数。则 ,莫比乌斯反演,得
,莫比乌斯反演,得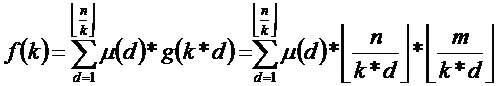 。
。 和
和 会有连续的一段相同且相同的为一定连续的一段,可证最多有2√n和2√m段,分块处理,对于每个询问可O(√n)解决。
会有连续的一段相同且相同的为一定连续的一段,可证最多有2√n和2√m段,分块处理,对于每个询问可O(√n)解决。
代码:
#include<cstdio>
#include<iostream>
using namespace std;
const int M=;
int k,prime[M],mu[M],s[M];
bool flag[M]; int read()
{
int x=; char ch=getchar();
while (ch<'' || ch>'') ch=getchar();
while (ch>='' && ch<='') x=(x<<)+(x<<)+ch-,ch=getchar();
return x;
} void getmu(int n)
{
mu[]=;
int i,j,k,cnt=;
for (i=;i<n;++i)
{
if (!flag[i]) prime[++cnt]=i,mu[i]=-;
for (j=;j<=cnt && (k=i*prime[j])<n;++j)
{
flag[k]=;
if (!(i%prime[j])) { mu[k]=; break; }
mu[k]=-mu[i];
}
}
for (i=;i<n;++i) s[i]=s[i-]+mu[i];
} int sum(int n,int m)
{
if (n>m) swap(n,m);
n=n/k,m=m/k;
int i,j,ans=;
for (i=;i<=n;i=j+)
{
j=min(n/(n/i),m/(m/i));
ans=ans+(s[j]-s[i-])*(n/i)*(m/i);
}
return ans;
} int main()
{
getmu(M);
for (int T=read();T;--T)
{
int a=read(),b=read(),c=read(),d=read();k=read();
printf("%d\n",sum(b,d)-sum(a-,d)-sum(c-,b)+sum(a-,c-));
}
return ;
}
[HAOI2011]Problem b 题解的更多相关文章
- BZOJ2298:[HAOI2011]problem a——题解
https://www.lydsy.com/JudgeOnline/problem.php?id=2298 https://www.luogu.org/problemnew/show/P2519 一次 ...
- BZOJ2301:[HAOI2011]Problem b——题解
http://www.lydsy.com/JudgeOnline/problem.php?id=2301 https://www.luogu.org/problemnew/show/P2522 对于给 ...
- BZOJ2301: [HAOI2011]Problem b[莫比乌斯反演 容斥原理]【学习笔记】
2301: [HAOI2011]Problem b Time Limit: 50 Sec Memory Limit: 256 MBSubmit: 4032 Solved: 1817[Submit] ...
- bzoj 2301: [HAOI2011]Problem b
2301: [HAOI2011]Problem b Time Limit: 50 Sec Memory Limit: 256 MB Submit: 3757 Solved: 1671 [Submit] ...
- HAOI2011 problem b
2301: [HAOI2011]Problem b Time Limit: 50 Sec Memory Limit: 256 MBSubmit: 1047 Solved: 434[Submit][ ...
- BZOJ 2298: [HAOI2011]problem a 动态规划
2298: [HAOI2011]problem a Time Limit: 1 Sec Memory Limit: 256 MB 题目连接 http://www.lydsy.com/JudgeOnli ...
- 【BZOJ2302】[HAOI2011]Problem C(动态规划)
[BZOJ2302][HAOI2011]Problem C(动态规划) 题面 BZOJ 洛谷 题解 首先如果\(m=0\)即没有特殊限制的话,那么就和这道题目基本上是一样的. 然而这题也有属于这题的性 ...
- [POI2007]ZAP-Queries && [HAOI2011]Problem b 莫比乌斯反演
1,[POI2007]ZAP-Queries ---题面---题解: 首先列出式子:$$ans = \sum_{i = 1}^{n}\sum_{j = 1}^{m}[gcd(i, j) == d]$$ ...
- 【BZOJ2298】[HAOI2011]problem a DP
[BZOJ2298][HAOI2011]problem a Description 一次考试共有n个人参加,第i个人说:“有ai个人分数比我高,bi个人分数比我低.”问最少有几个人没有说真话(可能有相 ...
随机推荐
- Ignatius and the Princess III HDU - 1028 || 整数拆分,母函数
Ignatius and the Princess III HDU - 1028 整数划分问题 假的dp(复杂度不对) #include<cstdio> #include<cstri ...
- SpringCloud开发学习总结(三)—— 服务治理Eureka
在最初开始构建微服务系统的时候可能服务并不多,我们可以通过做一些静态配置来完成服务的调用.比如,有两个服务A和B,其中服务A需要调用服务B来完成一个业务操作时,为了实现服务B的高可用,不论采用服务端负 ...
- Volley的初步了解
Volley的介绍 Volley是什么? 2013年Google I/O大会上推出的网络请求和图片加载框架 其优点是api简单,性能优秀 非常适合数据量不大但是通信频繁的网络请求,而对于大数据量的操作 ...
- AngularJS ng-repeat下使用ng-model
1 2 3 blue:<input type="radio" value="1" ng-model="selectValue"/> ...
- ATM机(非函数版)
#include<stdio.h>#include<stdlib.h>int main(void){char zhangHao[]="123";int mi ...
- Webform 内置对象 Response对象、Request对象,QueryString
Request对象:获取请求Request["key"]来获取传递过来的值 QueryString:地址栏数据传递 ?key=value&key=value注意事项:不需要 ...
- eclipse debug java 源码
当我们需要研究java SE的时候,debug 源码是个不错的选择,可以帮助我们清楚了解java 封装jar包的具体实现. 因为oracle 提供的源码jar包为了节省空间,所以没有将调试信息一起打包 ...
- php自动加载函数
含义:将函数注册到SPL __autoload函数栈中.如果该栈中的函数尚未激活,则激活它们. 先看__autoload 函数 printit.class.php <?php class PRI ...
- vue框架的知识
基础:实例----组件----指令----选项-----计算属性----事件绑定----模板渲染-----内置动画 ---组件交互----路由. vuejs干了什么事情:数据渲染/数据同步 组件化/模 ...
- 编写图形界面下的Java Swing程序,接受用户输入的两个数据为上下限,然后输出上、下限之间的所有素数。(结果部分每行显示10个数据)
这个代码我整体写的比较简单,读者可以简单参考一下,对人家题目要求略微修改了一下,多加了一个“置空”按钮.下图为我设计的界面 运行程序后的截图请看我后面的截图: package com.wangshil ...
