codeforces 689D D. Friends and Subsequences(RMQ+二分)

题目链接：

D. Friends and Subsequences

time limit per test

2 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Mike and !Mike are old childhood rivals, they are opposite in everything they do, except programming. Today they have a problem they cannot solve on their own, but together (with you) — who knows?

Every one of them has an integer sequences a and b of length n. Being given a query of the form of pair of integers (l, r), Mike can instantly tell the value of 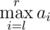 while !Mike can instantly tell the value of .

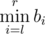Now suppose a robot (you!) asks them all possible different queries of pairs of integers (l, r) (1 ≤ l ≤ r ≤ n) (so he will make exactlyn(n + 1) / 2 queries) and counts how many times their answers coincide, thus for how many pairs 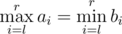 is satisfied.

How many occasions will the robot count?

 

Input

 

The first line contains only integer n (1 ≤ n ≤ 200 000).

The second line contains n integer numbers a1, a2, ..., an ( - 109 ≤ ai ≤ 109) — the sequence a.

The third line contains n integer numbers b1, b2, ..., bn ( - 109 ≤ bi ≤ 109) — the sequence b.

 

Output

 

Print the only integer number — the number of occasions the robot will count, thus for how many pairs 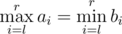 is satisfied.

Examples

 

input

6
1 2 3 2 1 4
6 7 1 2 3 2

output

2

input

3
3 3 3
1 1 1

output

0

题意：

在一个区间[l,r]中a的最大值等于b的最小值,问这样的区间有多少个;

思路：

枚举左端点,二分找到右端点可行区间的左右边界;
在确定右段点的左右边界时,要用RMQ,
左边界:要是amax>=bmin,左移;否则右移,找到第一个amax=bmin的点;
右边界：要是amax>bmin,左移,否则右移,找到最后一个amax=bmin的点;

累加右端点可行区间长度即可;

AC代码：

//#include <bits/stdc++.h>
#include <vector>
#include <iostream>
#include <queue>
#include <cmath>
#include <map>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
#define For(i,j,n) for(int i=j;i<=n;i++)
#define Riep(n) for(int i=1;i<=n;i++)
#define Riop(n) for(int i=0;i<n;i++)
#define Rjep(n) for(int j=1;j<=n;j++)
#define Rjop(n) for(int j=0;j<n;j++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
typedef  long long LL;
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<''||CH>'';F= CH=='-',CH=getchar());
    for(num=;CH>=''&&CH<='';num=num*+CH-'',CH=getchar());
    F && (num=-num);
}
int stk[], tp;
template<class T> inline void print(T p) {
    if(!p) { puts(""); return; }
    while(p) stk[++ tp] = p%, p/=;
    while(tp) putchar(stk[tp--] + '');
    putchar('\n');
}

const LL mod=1e9+;
const double PI=acos(-1.0);
const LL inf=1e18;
const int N=2e5+;
const int maxn=;
const double eps=1e-;

int a[N],b[N],MX[N][],MN[N][],n;
struct Tree
{
    int l,r;
    int mmax,mmin;
}tr[*N];

void build(int o,int L,int R)
{
    for(int i=;i<=n;i++)
    MX[i][]=a[i],MN[i][]=b[i];
    for(int j=;(<<j)<=n;j++)
    {
        for(int i=;i+(<<j)-<=n;i++)
        {
            MX[i][j]=max(MX[i][j-],MX[i+(<<(j-))][j-]);
            MN[i][j]=min(MN[i][j-],MN[i+(<<(j-))][j-]);
        }
    }
}
int query(int o,int L,int R,int flag)
{
    if(flag)
    {
        int k = ;
        while( (<<(k+)) <= R-L+) k ++ ;
        return max(MX[L][k],MX[R-(<<k)+][k]);
    }
    else
    {
        int k = ;
        while( (<<(k+)) <= R-L+) k ++ ;
        return min(MN[L][k],MN[R-(<<k)+][k]);
    }
}
int check(int x,int y,int flag)
{
    int mx=query(,x,y,),mn=query(,x,y,);
  if(flag){  if(mx==mn)return ;
            else if(mx>mn)return ;
                return ;}
    else
    {
        if(mx==mn)return ;
        return ;
    }
}
int main()
{
    read(n);
    For(i,,n)read(a[i]);
    For(i,,n)read(b[i]);
    build(,,n);
    LL ans=;
    int L,R;
    For(i,,n)
    {
        int l=i,r=n;
        while(l<=r)
        {
            int mid=(l+r)>>;
            if(!check(i,mid,))l=mid+;
            else r=mid-;
        }
        L=l;
        if(check(i,L,)==)continue;
        l=L,r=n;
        while(l<=r)
        {
            int mid=(l+r)>>;
            if(check(i,mid,))l=mid+;
            else r=mid-;
        }
        R=l-;
        if(R>=L)ans=ans+(R-L+);
    }
    cout<<ans<<"\n";
        return ;
}