显示效果如下：

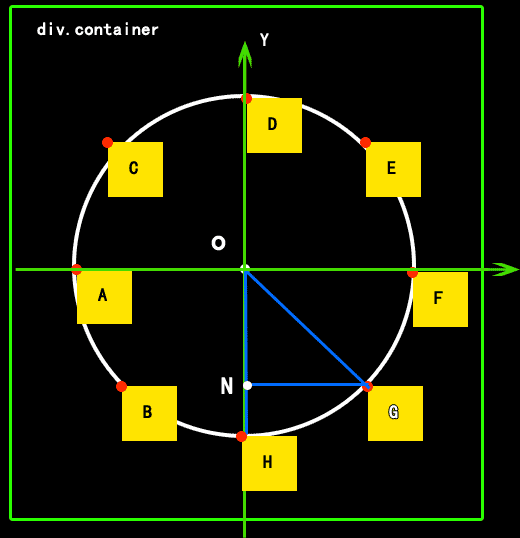
需要用到的知识：

等于半径长的圆弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度。用弧度作单位来度量角的制度叫做弧度制。另外一种度量角的方法是角度制。弧度制的精髓就在于统一了度量弧与半径的单位，从而大大简化了有关公式及运算，尤其在高等数学中，其优点就格外明显。

一个完整的圆的弧度是2π，所以2π rad = 360°，1 π rad = 180°，

我们平时用的sin(x); x为π/2是就相等于90°，为1.

sin,cos用弧度制方便一点。

var dotLeft = ($(".container").width()-$(".dot").width())/2; 为什么要减去$(".dot").width()
因为我们的圆心（中心点）也是一个div，不像上面画的就是一个点，中心div定位也是从左上角定位的。所有要减去。
<script type="text/javascript">

    $(function(){

        //中心点横坐标

        var dotLeft = ($(".container").width()-$(".dot").width())/2;

        //中心点纵坐标

        var dotTop = ($(".container").height()-$(".dot").height())/2;

        //起始角度

        var stard = 0;

        //半径

        var radius = 200;

        //每一个BOX对应的角度;

        var avd = 360/$(".box").length;

        //每一个BOX对应的弧度;

        var ahd = avd*Math.PI/180;

        console.log(Math.sin(ahd*2));

        console.log(Math.sin(ahd*6));

        console.log(Math.cos(ahd*2));

        console.log(Math.cos(ahd*3));

        //设置圆的中心点的位置

        $(".dot").css({"left":dotLeft,"top":dotTop});

        $(".box").each(function(index, element){

            $(this).css({"left":Math.sin((ahd*index))*radius+dotLeft,"top":Math.cos((ahd*index))*radius+dotTop});

        });

    })

</script>

<style type="text/css">

*{margin:0;padding:0;}

.container{position:relative;width:700px;height:800px; margin:0 auto; border:1px solid #F00;}

.box{position:absolute;width:50px;height:50px;background:#000;}

.dot{ position:absolute;width:20px;height:20px;background:#F00;}

</style>

</head>

<body>

<div class="container">

    <div class="dot"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

    <div class="box"></div>

</div>

</body>

参考；http://www.cnblogs.com/lufy/archive/2012/06/21/2558049.html

javascript圆形排列的更多相关文章

  1. javascript 获取排列后的对象建值

    function getSortedParameter (parameterObject){ let attributes = []; parameterObject = parameterObjec ...

  2. javascript 中的原型继承

    javascript圆形变成的基本规则: 所有数据都是对象: 要得到一个对象,不是通过实例化类,而是找到一个对象作为原型并克隆它: 对象会记住它的原型: 如果对象无法响应某个请求,它会把这个请求委托给 ...

  3. div 环形排列

    javascript-按圆形排列DIV元素(一)---- 分析 效果图: 一.分析图: 绿色边框内:外层的DIV元素,相对定位; 白色圆形框:辅助分析的想象形状; 白点:为白色圆形的圆心点,中心点,点 ...

  4. [组合数学] 圆排列和欧拉函数为啥有关系：都是polya定理的锅

    本文是一个笨比学习组合数学的学习笔记,因为是笨比,所以写的应该算是很通俗易懂了. 首先,我们考虑这么一个问题:你有无穷多的\(p\)种颜色的珠子,现在你想要的把他们中的\(n\)个以圆形的形状等间距的 ...

  5. HTML5印章绘制电子签章图片，中文英文椭圆章、中文英文椭圆印章

    原文:HTML5印章绘制电子签章图片,中文英文椭圆章.中文英文椭圆印章 电子签章图片采集 印章图片的采集两种互补方式: 方式1:在线生成印章图片方式,但是这种方式有个弊端,对印章中公司名称字数有限制, ...

  6. 简答的理解C语言中的各种类型函数

    1.变参函数 变长参数的函数即参数个数可变.参数类型不定 的函数.最常见的例子是printf函数.scanf函数和高级语言的Format函数.在C/C++中,为了通知编译器函数的参数个数和类型可变(即 ...

  7. 2016CVTE编程题：兔子藏洞

    兔子藏洞 题目描述 一只兔子藏身于20个圆形排列的洞中(洞从1开始编号),一只狼从x号洞开始找,下次隔一个洞找(及在x+2号洞找),在下次个两个洞找(及在x+5号洞找),以此类推...它找了n次仍然没 ...

  8. WPF 图片浏览 伪3D效果

    原文:WPF 图片浏览 伪3D效果 首先上效果图: 因项目要求,需要把图片以"好看"."炫"的效果展示出来,特地研究了一下WPF关于3D方面的制作,奈何最终成果 ...

  9. [bzoj1488][HNOI2009]图的同构——Polya定理

    题目大意 求两两互不同构的含n个点的简单图有多少种. 简单图是关联一对顶点的无向边不多于一条的不含自环的图. a图与b图被认为是同构的是指a图的顶点经过一定的重新标号以后,a图的顶点集和边集能完全与b ...

随机推荐

  1. 连接Xively云

    1.注册Xively开发账号 在https://xively.com注册一个开发账户,收到激活邮件后激活,注意,如果登陆后无法进入develop页面,请退出重新登陆. 2.添加设备 3.获取FeedI ...

  2. 创建以 API 为中心的 Web 应用

    http://www.oschina.net/translate/creating-an-api-centric-web-application?from=20130818 正计划着要开始搞一个新的网 ...

  3. Delphi反汇编内部字符串处理函数不完全列表

    Delphi反汇编内部字符串处理函数/过程不完全列表 名称 参数 返回值 作用 等价形式 / 备注 _PStrCat EAX :目标字符串 EDX :源字符串 EAX 连接两个 Pascal 字符串 ...

  4. Genymotion如何访问本地服务器？

    找到原因了,其实跟Genymotion没有关系,因为他本身是作为VirtualBox的一个虚拟OS在运行. 默认情况下,查看Genymotion的网络配置,是Host-Only模式: Microsof ...

  5. 协方差cov

    摘录wiki如下(红色字体是特别标注的部分): http://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE 协方差 协方差(Covariance) ...

  6. unity3d导出pdf

    unity生成pdf格式,首先需要导入iTextSharp.dll ,下面是我写的一些方法,可以直接用.直接贴代码, using UnityEngine; using System.Collectio ...

  7. javascript第十五课：DOM

    dom就是文档,就是整个网页的简称,dom里面的标签就是对象 使用javascript进行DHMTL网页开发(Dynamic Html 动态网页) dom就是把html页面模拟成一个对象,顶级对象wi ...

  8. Fast RCNN 学习

    因为项目需要,之前没有接触过深度学习的东西,现在需要学习Fast RCNN这个方法. 一步步来,先跟着做,然后再学习理论 Fast RCNN 训练自己数据集 (1编译配置) Fast RCNN 训练自 ...

  9. kindeditor 下图片链接取消边框

    在项目中使用了 kindeditor,版本是4.1.10,在发布信息的时候,将图片设置成了超链接,在 IE8 或者其他个别浏览器下会自动的为图片加一个蓝色的边框,效果如下图: 这个蓝框可以通过修改信息 ...

  10. EnyimMemcached扩展 遍历功能

    Memcached本身对外提供的命令不多,也就add.get.set.incr.decr.replace.delete.stats等几个,客户端对这些操作进行了封装,总体来说调用还是很简单的. 初看了 ...