【NOI2019模拟2019.7.1】三格骨牌（轮廓线dp转杨图上钩子定理）

Description

---

\(n,m<=1e4,mod ~1e9+7\)

题解：

---

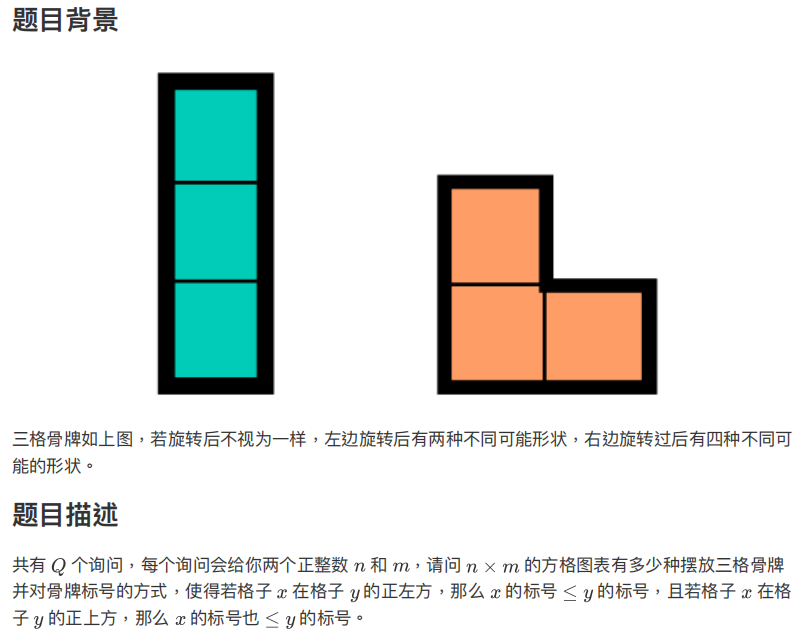
显然右边那个图形只有旋转90°和270°后才能放置。

先考虑一个暴力的轮廓线dp：

假设已经放了编号前i的骨牌，那么这些骨牌形成的图形一定是杨表那样的。

对轮廓线来考虑，不妨设1表示向上走，0表示向右走。

初始状态是：111…(n个1)000..(m个0)

那么四种转移为：

1. 1110->0111
2. 1000->0001
3. 1010->0011
4. 1100->0101

这样暴力dp应该能过n,m<=10的。

观察这四种转移，中间的两位都不变，只是把第1位的1移到第4位。

那么按\(mod~3\)分开做，问题变为有一个x+y长的01序列，一开始是x个1+y个0.

每次可以把一个1和紧接的0交换，求最后变为x个0+y个1的方案数。

再把这个转到x×y的杨图上去，一开始轮廓线紧贴左边界和上边界，每次可以把轮廓线的一行改宽一列，且还要满足轮廓线的性质，其实这就是x×y的杨图个数，套钩子定理即可。

那么\(Ans=(xy)!/\prod_{i=0}^{n-1}\prod_{j=1}^{m-1}(i+j+1)!\)

Code：

---

#include <bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define fi first
#define se second
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=1000000007;
ll powmod(ll a,ll b) {ll res=1;a%=mod;for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
int fac[34000100];
int _,n,m;
int main() {
	freopen("trominoes.in", "r", stdin);
	freopen("trominoes.out", "w", stdout);
    ll s=1;
    fac[0]=1;
    rep(i,1,34000000) fac[i]=(ll)fac[i-1]*i%mod;
    for (scanf("%d",&_);_;_--) {
        scanf("%d%d",&n,&m);
        if (n*m%3!=0) {
            puts("0");
            continue;
        }
        if (n%3!=0) swap(n,m);
        ll ret=fac[n*m/3],rg=1;
        rep(i,0,m) {
            ret=ret*fac[i/3]%mod;
            rg=rg*fac[i/3+n/3]%mod;
        }
        ret=ret*powmod(rg,mod-2)%mod;
        printf("%lld\n",ret);
    }
}