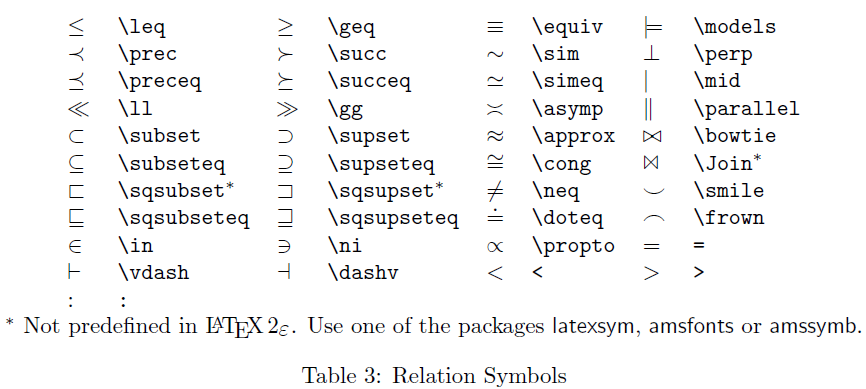
Markdown转义字符表









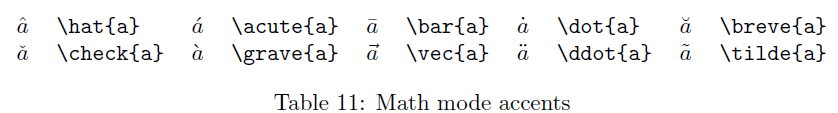



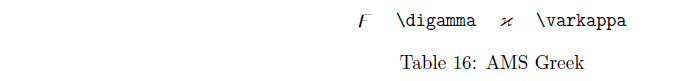

Markdown转义字符表的更多相关文章
- 常用HTML转义字符,html转义符,JavaScript转义符,html转义字符表,HTML语言特殊字符对照表(ISO Latin-1字符集)
HTML字符实体(Character Entities),转义字符串(Escape Sequence) 为什么要用转义字符串? HTML中<,>,&等有特殊含义(<,> ...
- C/C++转义字符表
转义字符 意义 ASCII码值(十进制) \a 响铃(BEL) 007 \b 退格(BS) ,将当前位置移到前一列 008 \f 换页(FF),将当前位置移到下页开头 012 \n 换行(LF) ,将 ...
- markdown 转义字符
\\ 反斜杠 \` 反引号 \* 星号 \_ 下划线 \{\} 大括号 \[\] 中括号 \(\) 小括号 \# 井号 \+ 加号 \- 减号 \. 英文句号 \! 感叹号
- HTML转义字符表
- C语言转义字符表和ASCII码表
主要参考 http://www.51hei.com/mcu/4342.html 以及 https://www.cnblogs.com/jason207489550/p/6663444.html
- Markdown中特殊字符的转义字符
上次在用Markdown记笔记时,当正文中写到<PROJECT>_<PATH>_<FILE>_H_时,<>里的内容显示显示不出来,就算用' '也显示不出 ...
- (1)HTML的组成(什么是标签、指令、转义字符、数据、标签字符表)
html的组成:标签+指令+转义字符+数据 1.标签 <>内的,以字母开头,可以结合合法字符(- 或者数字),能被浏览器解析的符号 <!DOCTYPE html> #这个是系统 ...
- Markdown简记
一篇好的博客文档离不开一个优秀的编辑器.借此篇文章介绍一下编写该博客markdown的语法,方便大家写出更好更漂亮的文档.重点是点击左上角的Github链接,有主题源码哦 一篇好的博客文档离不开一个优 ...
- Markdown用法说明(用此篇博客做示例)
一份好的博客文档离不开一个优秀的编辑器.借此篇文章介绍一下编写该博客markdown的语法,后续再增加介绍其他语法,方便大家写出更好更漂亮的文档.点击左上角github,有主题源码哦 一份好的博客文档 ...
随机推荐
- iOS录音后播放声音变小的解决方法
目前需求是录音之后再播放出来.经常会出现播放声音变很小的情况. 解决方法: if (recorder.recording){ [recorder stop]; } [[AVAudioSession s ...
- EE5111_A0206839W
EE5111 Selected Topics in Industrial Control & Instrumentation Assessment: Implement a simple ...
- 用IP地址访问共享文件
一.用WIN+R 打开运行,如图输入地址: 二.输入用户名和密码就打开共享文件夹了
- leetcood学习笔记-167-两数之和 II - 输入有序数组
题目描述: 第一次提交: class Solution(object): def twoSum(self, numbers, target): """ :type num ...
- SQL Server 中根据字段值查询其所在的表、字段
DECLARE @what varchar(800)SET @what='123456' --要搜索的字符串 DECLARE @sql varchar(8000) DECLARE TableC ...
- Ruby 环境
Ruby 环境 本地环境设置 如果您想要设置 Ruby 编程语言的环境,请阅读本章节的内容.本章将向您讲解与环境设置有关的所有重要的主题.建议先学习下面几个主题,然后再进一步深入学习其他主题: Lin ...
- Java高新技术第三篇:注解的使用
我们知道注解是在JDK1.5引入的,可能有的人没有用过注解,所以感觉注解这个东西没有什么用,但是深入了解注解,对以后学习框架有所帮助的,后面提到的JavaWeb的框架中很多都是基于注解的技术, 其实注 ...
- Noip 2012 day2t1 同余方程
Description 求关于x的同余方程ax ≡ 1 (mod b)的最小正整数解. Input 输入文件为mod.in. 输入只有一行,包含两个正整数 a, b,用一个空格隔开. Output 输 ...
- NX二次开发-UFUN将工程图中的点坐标映射到建模绝对坐标UF_VIEW_map_drawing_to_model
#include <uf.h> #include <uf_ui.h> #include <uf_draw.h> #include <uf_view.h> ...
- 解决php-fpm占用cpu memory过高,开启php-fpm request_slowlog_timeout
项目刚从win下挪到linux下,发现cpu过高,内存也占用较多,以下是我解决问题的过程: 首先更改php-fpm配置 vim /usr/local/php/etc/php-fpm.conf 找到 r ...
