（学习1）最小生成树-Prim算法与Kruskal算法

最小生成树：

求一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边.

1：Prim算法（适合稠密图）

伪代码：

Prim(G){   //G为图

       int addnow[maxen];//记录当前有多少点被纳入集合；

       int lowcost[maxen]; //记录当前集合中的点到其他点的最小距离的边集合；

       init();//初始化点集合与边集合；

       addnow[start]=true; //将起点纳入点集合

       for(i=;i<G.vertex;i++){  //还剩下n-1个点需要归并

           Min=;

           for(j=;j<=G.vertex;j++){ 

                if(!addnow[j]&&lowcost[j]<minn) {    //寻找权值最小并且点未被归并的边

                 minn=addnow[j];

　　          index=j;         }

           }

        addnow[index]=; //将该点加入集合

        updateV();//因为点集合新入点，故需要更新该集合到其他点的距离

      }

}

解析：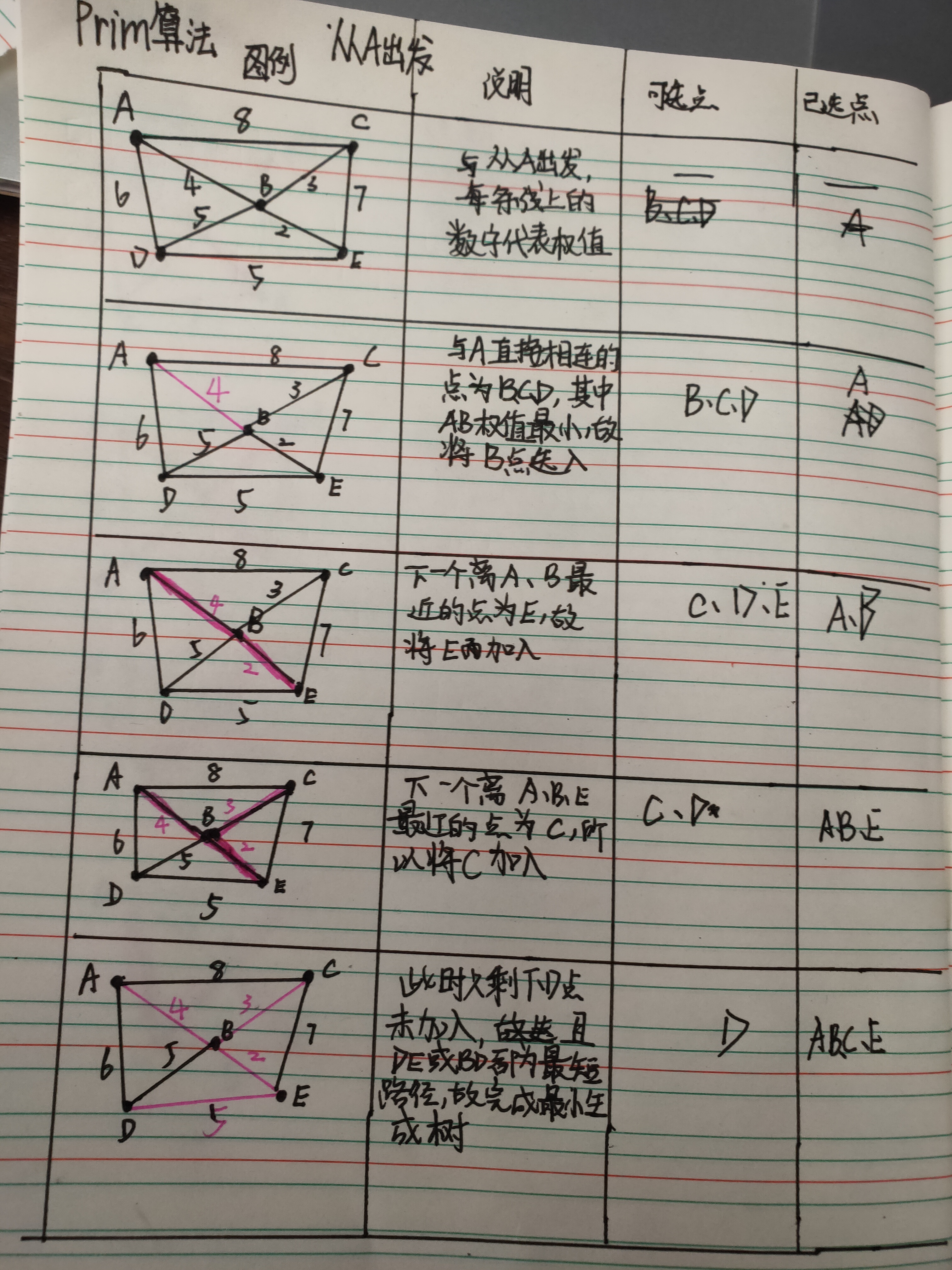                                               

时间复杂度：O（n²）

Kruskal算法（适合稀疏图）

伪代码:(n为顶点数)

Kruskal(G){
   for(i->G.edge.num){
        if(find([G.edge.start])!=find([G.edge.end])){  //若没形成闭环
             find([G.edge.end])=find([G.edge.start]);  //将边加入路径
       }
       if(edgeNum==G.vertex.num-)    //若已经找到n-1条边则退出
          break;
   }
}

解析：

时间复杂度：o(nlogn)

github源码地址:

https://github.com/yizhihenpidehou/bananas/tree/master/%E7%AC%AC%E4%B8%80%E5%91%A8-%E5%8F%B6%E6%B3%A2%E7%94%B8