机器学习作业(二)逻辑回归——Matlab实现
题目太长啦!文档下载【传送门】
第1题
简述:实现逻辑回归。
第1步:加载数据文件:
data = load('ex2data1.txt');
X = data(:, [1, 2]); y = data(:, 3);
plotData(X, y);
% Put some labels
hold on;
% Labels and Legend
xlabel('Exam 1 score')
ylabel('Exam 2 score')
% Specified in plot order
legend('Admitted', 'Not admitted')
hold off;
第2步:plotData函数实现训练样本的可视化:
function plotData(X, y)
% Create New Figure
figure;
hold on; pos = find(y==1);
neg = find(y==0);
plot(X(pos,1),X(pos,2),'k+','LineWidth',2,'MarkerSize',7);
plot(X(neg,1),X(neg,2),'ko','MarkerFaceColor','y','MarkerSize',7); hold off;
end
第3步:计算代价函数和梯度:
% Setup the data matrix appropriately, and add ones for the intercept term
[m, n] = size(X); % Add intercept term to x and X_test
X = [ones(m, 1) X]; % Initialize fitting parameters
initial_theta = zeros(n + 1, 1); % Compute and display initial cost and gradient
[cost, grad] = costFunction(initial_theta, X, y);
第4步:实现costFunction函数:
function [J, grad] = costFunction(theta, X, y) m = length(y); % number of training examples
J = 0;
grad = zeros(size(theta)); h = sigmoid(X*theta);
J = 1/m*(-y'*log(h)-(1-y')*log(1-h));
grad = 1/m*(X'*(h-y)); end
第5步:实现sigmoid函数:
function g = sigmoid(z)
g = zeros(size(z));
g = 1./(1+exp(-z));
end
第6步:使用fminunc函数求θ和Cost:
% Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 400); % Run fminunc to obtain the optimal theta
% This function will return theta and the cost
[theta, cost] = ...
fminunc(@(t)(costFunction(t, X, y)), initial_theta, options); % Print theta to screen
fprintf('Cost at theta found by fminunc: %f\n', cost);
fprintf('theta: \n');
fprintf(' %f \n', theta); % Plot Boundary
plotDecisionBoundary(theta, X, y); % Put some labels
hold on;
% Labels and Legend
xlabel('Exam 1 score')
ylabel('Exam 2 score') % Specified in plot order
legend('Admitted', 'Not admitted')
hold off;
第7步:实现plotDecisionBoundary函数:
function plotDecisionBoundary(theta, X, y) % Plot Data
plotData(X(:,2:3), y);
hold on if size(X, 2) <= 3
% Only need 2 points to define a line, so choose two endpoints
plot_x = [min(X(:,2))-2, max(X(:,2))+2]; % Calculate the decision boundary line
plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1)); % Plot, and adjust axes for better viewing
plot(plot_x, plot_y) % Legend, specific for the exercise
legend('Admitted', 'Not admitted', 'Decision Boundary')
axis([30, 100, 30, 100])
else
% Here is the grid range
u = linspace(-1, 1.5, 50);
v = linspace(-1, 1.5, 50); z = zeros(length(u), length(v));
% Evaluate z = theta*x over the grid
for i = 1:length(u)
for j = 1:length(v)
z(i,j) = mapFeature(u(i), v(j))*theta;
end
end
z = z'; % important to transpose z before calling contour % Plot z = 0
% Notice you need to specify the range [0, 0]
contour(u, v, z, [0, 0], 'LineWidth', 2)
end
hold off end
运行结果:
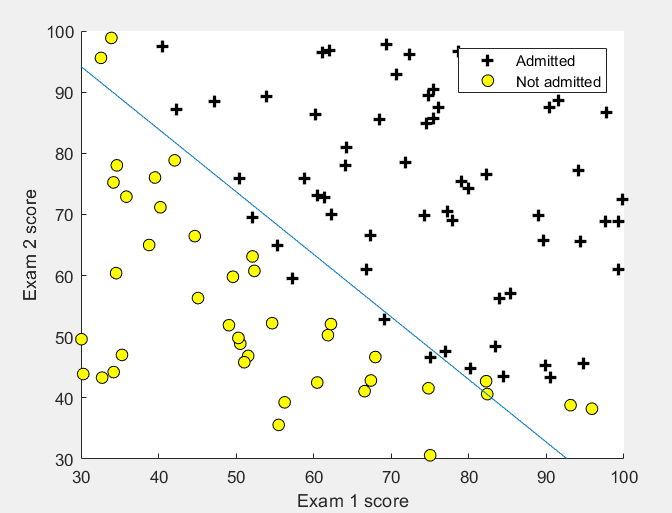
第8步:预测[45 85]成绩的学生,并计算准确率:
prob = sigmoid([1 45 85] * theta);
fprintf(['For a student with scores 45 and 85, we predict an admission ' ...
'probability of %f\n'], prob);
fprintf('Expected value: 0.775 +/- 0.002\n\n'); % Compute accuracy on our training set
p = predict(theta, X); fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);
fprintf('Expected accuracy (approx): 89.0\n');
fprintf('\n');
第9步:实现predict预测函数:
function p = predict(theta, X)
m = size(X, 1); % Number of training examples
p = zeros(m, 1);
p = round(sigmoid(X*theta));
end
运行结果:

第2题
简述:通过正规化实现逻辑回归。
第1步:加载数据文件:
data = load('ex2data2.txt');
X = data(:, [1, 2]); y = data(:, 3);
plotData(X, y);
% Put some labels
hold on;
% Labels and Legend
xlabel('Microchip Test 1')
ylabel('Microchip Test 2')
% Specified in plot order
legend('y = 1', 'y = 0')
hold off;
第2步:正规化逻辑回归:
% Note that mapFeature also adds a column of ones for us, so the intercept
% term is handled
X = mapFeature(X(:,1), X(:,2)); % Initialize fitting parameters
initial_theta = zeros(size(X, 2), 1); % Set regularization parameter lambda to 1
lambda = 1; % Compute and display initial cost and gradient for regularized logistic
% regression
[cost, grad] = costFunctionReg(initial_theta, X, y, lambda); fprintf('Cost at initial theta (zeros): %f\n', cost);
fprintf('Gradient at initial theta (zeros) - first five values only:\n');
fprintf(' %f \n', grad(1:5));
第3步:mapFeature函数实现特征设置:
function out = mapFeature(X1, X2) degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
for j = 0:i
out(:, end+1) = (X1.^(i-j)).*(X2.^j);
end
end end
其设置的特征值为:
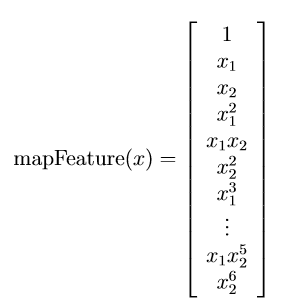
第4步:实现costFunctionReg函数:
function [J, grad] = costFunctionReg(theta, X, y, lambda) % Initialize some useful values
m = length(y); % number of training examples % You need to return the following variables correctly
J = 0;
grad = zeros(size(theta)); theta2 = theta(2:end,1);
h = sigmoid(X*theta);
J = 1/m*(-y'*log(h)-(1-y')*log(1-h)) + lambda/(2*m)*sum(theta2.^2);
theta(1,1) = 0;
grad = 1/m*(X'*(h-y)) + lambda/m*theta; end
第5步:使用fminunc函数求θ和Cost,并预测准确率:
% Initialize fitting parameters
initial_theta = zeros(size(X, 2), 1); % Set regularization parameter lambda to 1 (you should vary this)
lambda = 1; % Set Options
options = optimset('GradObj', 'on', 'MaxIter', 400); % Optimize
[theta, J, exit_flag] = ...
fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options); % Plot Boundary
plotDecisionBoundary(theta, X, y);
hold on;
title(sprintf('lambda = %g', lambda)) % Labels and Legend
xlabel('Microchip Test 1')
ylabel('Microchip Test 2') legend('y = 1', 'y = 0', 'Decision boundary')
hold off; % Compute accuracy on our training set
p = predict(theta, X); fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);
fprintf('Expected accuracy (with lambda = 1): 83.1 (approx)\n');
运行结果:
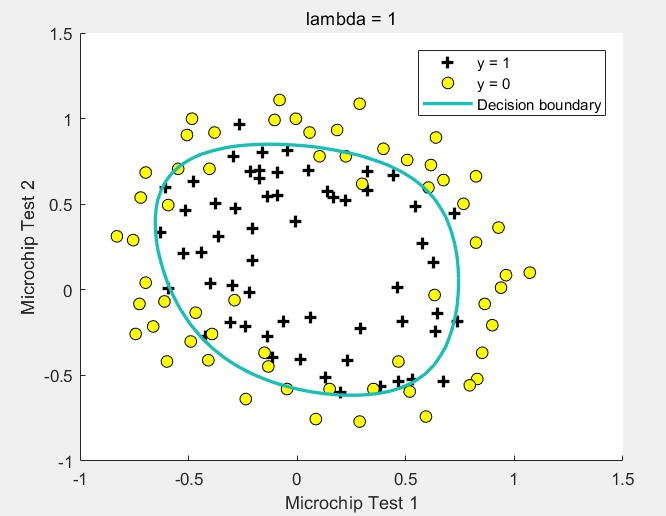

机器学习作业(二)逻辑回归——Matlab实现的更多相关文章
- 机器学习二 逻辑回归作业、逻辑回归(Logistic Regression)
机器学习二 逻辑回归作业 作业在这,http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/hw2.pdf 是区分spam的. 57 ...
- 机器学习总结之逻辑回归Logistic Regression
机器学习总结之逻辑回归Logistic Regression 逻辑回归logistic regression,虽然名字是回归,但是实际上它是处理分类问题的算法.简单的说回归问题和分类问题如下: 回归问 ...
- Coursera-AndrewNg(吴恩达)机器学习笔记——第三周编程作业(逻辑回归)
一. 逻辑回归 1.背景:使用逻辑回归预测学生是否会被大学录取. 2.首先对数据进行可视化,代码如下: pos = find(y==); %找到通过学生的序号向量 neg = find(y==); % ...
- scikit-learn机器学习(二)逻辑回归进行二分类(垃圾邮件分类),二分类性能指标,画ROC曲线,计算acc,recall,presicion,f1
数据来自UCI机器学习仓库中的垃圾信息数据集 数据可从http://archive.ics.uci.edu/ml/datasets/sms+spam+collection下载 转成csv载入数据 im ...
- Stanford机器学习---第三讲. 逻辑回归和过拟合问题的解决 logistic Regression & Regularization
原文:http://blog.csdn.net/abcjennifer/article/details/7716281 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...
- 【机器学习基础】逻辑回归——LogisticRegression
LR算法作为一种比较经典的分类算法,在实际应用和面试中经常受到青睐,虽然在理论方面不是特别复杂,但LR所牵涉的知识点还是比较多的,同时与概率生成模型.神经网络都有着一定的联系,本节就针对这一算法及其所 ...
- 机器学习入门11 - 逻辑回归 (Logistic Regression)
原文链接:https://developers.google.com/machine-learning/crash-course/logistic-regression/ 逻辑回归会生成一个介于 0 ...
- Spark机器学习(2):逻辑回归算法
逻辑回归本质上也是一种线性回归,和普通线性回归不同的是,普通线性回归特征到结果输出的是连续值,而逻辑回归增加了一个函数g(z),能够把连续值映射到0或者1. MLLib的逻辑回归类有两个:Logist ...
- Logistic回归二分类Winner or Losser----台大李宏毅机器学习作业二(HW2)
一.作业说明 给定训练集spam_train.csv,要求根据每个ID各种属性值来判断该ID对应角色是Winner还是Losser(0.1分类). 训练集介绍: (1)CSV文件,大小为4000行X5 ...
随机推荐
- Python3标准库:functools管理函数的工具
1. functools管理函数的工具 functools模块提供了一些工具来调整或扩展函数和其他callable对象,从而不必完全重写. 1.1 修饰符 functools模块提供的主要工具就是pa ...
- java工作流系统jflow表单引擎字段扩展组件介绍
关键词:工作流快速开发平台 工作流流设计 业务流程管理 asp.net 开源工作流 bpm工作流系统 java工作流主流框架 自定义工作流引擎 表单设计器 流程设计器 装饰类图片 用于 ...
- 在centos7上安装hadoop
1.使用hadoop是需要jdk环境的,因为hadoop里面有java程序,而运行java程序需要jdk. 2.从宿主机上传文件到虚拟机有很多方法,我选择的是在虚拟机安装lrzsz,安装lrzsz命令 ...
- Java数据结构--双向链表的实现
#java学习经验总结------双向链表的实现 双向链表的建立与单链表类似,只是需要使用pre指针指向前一个结点,并且在删除添加时不仅仅考虑next package datastructure; p ...
- 非常简洁简单的tcp socket库 XKSocket
一个非常简洁简单的异步tcp socket库,主要就是分包的问题,处理组包,粘包等问题 非常适合新手:) 项目中带有使用示例. http://git.oschina.net/dreamzgj/XKSo ...
- Vue之计算属性Computed和属性监听Watch,Computed和Watch的区别
一. 计算属性(computed) 1.计算属性是为了模板中的表达式简洁,易维护,符合用于简单运算的设计初衷. 例如: <div id="app"> {{ myname ...
- kettle:The tablename is not defined (empty)
报错误The tablename is not defined (empty) 去掉表输出中的"表分区数据"
- 为什么我用Ipad Pro做电子笔记和看PDF电子书
为什么我用Ipad Pro做电子笔记和看PDF电子书 Ipad做笔记的优点: 1.ipad整理的笔记可以随时修改,可以看PDF的书,2.纸质书很重携带不便3.ipad的可通过关键词搜索笔记内容 4.笔 ...
- 41.Python中加载静态文件
在一个网页中,不仅仅只有一个html骨架,还需要css样式文件,js执行文件以及一些图片等.因此在DTL中加载静态文件时一个必须要解决的问题.在DTL中,使用static标签来加载静态文件.要使用st ...
- bootstrap234的ie兼容选择
如果你需要兼容IE8甚至是IE7和IE6,那么只能选择Bootstrap2,虽然它自身在IE6的效果也并不完美.如果需要兼容IE678的话用2.如果需要高版本的浏览器,并且移动端优先的话,那么用boo ...
