B样条曲线曲面(附代码)
1 B样条曲线
1.1 B样条曲线方程
B样条方法具有表示与设计自由型曲线曲面的强大功能,是形状数学描述的主流方法之一,另外B样条方法是目前工业产品几何定义国际标准——有理B样条方法 (NURBS)的基础。B样条方法兼备了Bezier方法的一切优点,包括几何不变性,仿射不变性等等,同时克服了Bezier方法中由于整体表示带来不具有局部性质的缺点(移动一个控制顶点将会影响整个曲线)。B样条曲线方程可表示为
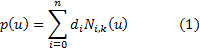
其中,di(i=0,1...n)为控制顶点(坐标),Ni,k(i=0,1...n)为k次规范B样条基函数,最高次数是k。基函数是由一个称为节点矢量的非递减参数u的序列U:u0≤u1≤...≤un+k+1所决定的k次分段多项式。
B样条的基函数通常采用Cox-deBoor递推公式:
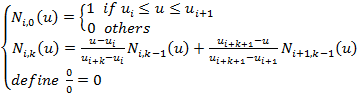 (2)
(2)
式中i为节点序号,k是基函数的次数,共有n+1个控制顶点。注意区分节点和控制顶点,节点是在节点矢量U中取得,控制顶点则是坐标点,决定B样条的控制多边形。Cox-deBoor递推公式是B样条曲线的定义的核心,该公式在程序中的实现可采用递归的方式:
function Nik_u = BaseFunction(i, k , u, NodeVector)
% 计算基函数Ni,k(u),NodeVector为节点向量 if k == 0 % 0次B样条
if (u >= NodeVector(i+1)) && (u < NodeVector(i+2))
Nik_u = 1.0;
else
Nik_u = 0.0;
end
else
Length1 = NodeVector(i+k+1) - NodeVector(i+1);
Length2 = NodeVector(i+k+2) - NodeVector(i+2); % 支撑区间的长度
if Length1 == 0.0 % 规定0/0 = 0
Length1 = 1.0;
end
if Length2 == 0.0
Length2 = 1.0;
end
Nik_u = (u - NodeVector(i+1)) / Length1 * BaseFunction(i, k-1, u, NodeVector) ...
+ (NodeVector(i+k+2) - u) / Length2 * BaseFunction(i+1, k-1, u, NodeVector);
end
Cox-deBoor递推公式
所给程序可用于计算基函数Ni,k(u)的值,程序中对不同类型的B样条曲线区别在于节点矢量 NodeVector 的取值不同。
1.2 B样条曲线的分类
根据节点矢量中节点的分布情况不同,可以划分4中类型的B样条曲线。不同类型的B样条曲线区别主要在于节点矢量,对于具有n+1个控制顶点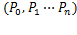 的 k 次B样条曲线,无论是哪种类型都具有n+k+2个节点
的 k 次B样条曲线,无论是哪种类型都具有n+k+2个节点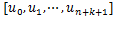 。
。
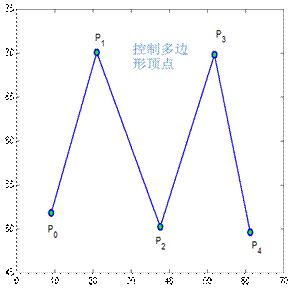
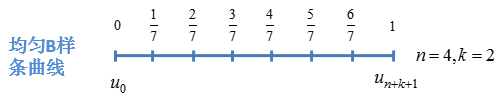
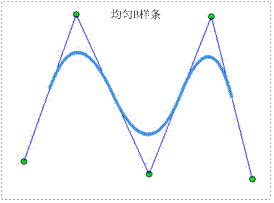
均匀B样条曲线
节点矢量中节点为沿参数轴均匀或等距分布。
对应的节点矢量: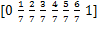
准均匀B样条曲线
其节点矢量中两端节点具有重复度k+1,即u0=u1=...=uk,un+1=un+2=...=un+k+1,所有的内节点均匀分布,具有重复度1。
对应的节点矢量: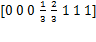
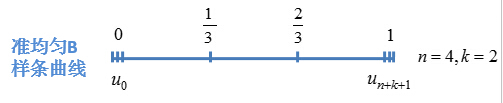
分段Bezier曲线
其节点矢量中两端节点的重复度与类型2相同,为k+1。不同的是内节点重复度为k。该类型有限制条件,控制顶点数减1必须等于次数的正整数倍,即必须满足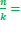 正整数。
正整数。
对应的节点矢量: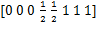
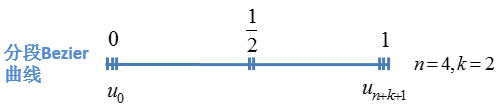
一般非均匀B样条曲线
对任意分布的节点矢量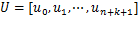 ,只要在数学上成立都可选取。
,只要在数学上成立都可选取。
这里给出准均匀B样条和分段Bezier曲线的生成节点矢量的代码,均匀B样条的很简单就不列出了。假设共n+1个控制顶点,k次B样条,输入参数为 n, k ,输出节点矢量到NodeVector中。
function NodeVector = U_quasi_uniform(n, k)
% 准均匀B样条的节点向量计算,共n+1个控制顶点,k次B样条
NodeVector = zeros(1, n+k+2);
piecewise = n - k + 1; % 曲线的段数
if piecewise == 1 % 只有一段曲线时,n = k
for i = n+2 : n+k+2
NodeVector(1, i) = 1;
end
else
flag = 1; % 不止一段曲线时
while flag ~= piecewise
NodeVector(1, k+1+flag) = NodeVector(1, k + flag) + 1/piecewise;
flag = flag + 1;
end
NodeVector(1, n+2 : n+k+2) = 1;
end
准均匀B样条节点向量
function NodeVector = U_piecewise_Bezier(n, k)
% 分段Bezier曲线的节点向量计算,共n+1个控制顶点,k次B样条
% 分段Bezier端节点重复度为k+1,内间节点重复度为k,且满足n/k为正整数 if ~mod(n, k) && (~mod(k, 1) && k>=1) % 满足n是k的整数倍且k为正整数
NodeVector = zeros(1, n+k+2); % 节点矢量长度为n+k+2
NodeVector(1, n+2 : n+k+2) = ones(1, k+1); % 右端节点置1 piecewise = n / k; % 设定内节点的值
Flg = 0;
if piecewise > 1
for i = 2 : piecewise
for j = 1 : k
NodeVector(1, k+1 + Flg*k+j) = (i-1)/piecewise;
end
Flg = Flg + 1;
end
end else
fprintf('error!\n');
end
分段Bezier曲线的节点向量
1.3 B样条曲线的计算
根据B样条曲线的定义公式(1),曲线上任一点坐标值是参数变量u的函数,用矩阵形式表示
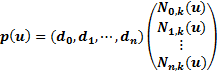 (3)
(3)
可以看出只要已知控制顶点坐标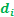 、曲线的次数
、曲线的次数 以及基函数
以及基函数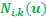 ,就完全确定了B样条曲线,其中基函数
,就完全确定了B样条曲线,其中基函数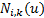 由Cox-deBoor 公式(2)递推计算。
由Cox-deBoor 公式(2)递推计算。
2 B样条曲面
2.1 B样条曲面方程
确定一张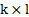 次张量积B样条曲面需要三个信息:
次张量积B样条曲面需要三个信息:
- 给定
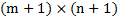 个控制顶点
个控制顶点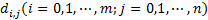 构成控制网格
构成控制网格 - 给定参数
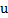 和
和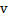 的次数
的次数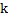 与
与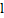
- u向和v向的节点矢量
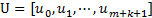 ,
,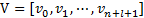
定义的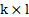 次张量积B样条曲面其方程为:
次张量积B样条曲面其方程为:
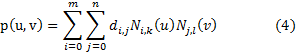
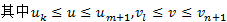 ,B样条基
,B样条基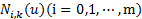 与
与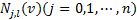 分别由节点矢量
分别由节点矢量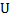 和
和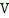 按Cox-deBoor递推公式(2)计算。
按Cox-deBoor递推公式(2)计算。
B样条曲面按照沿参数方向u, v所取的节点矢量不同,也可以划分成不同的类型:均匀、准均匀、分片Bezier和非均匀B样条曲面。
2.2 B样条曲面的计算
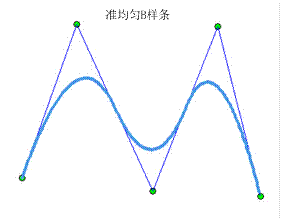
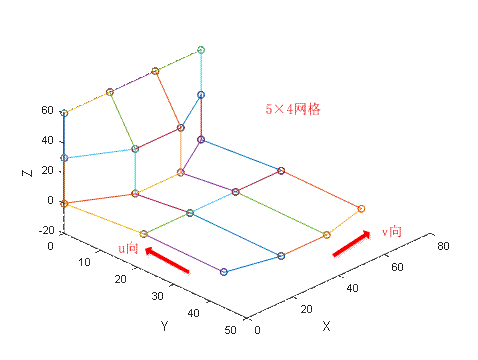
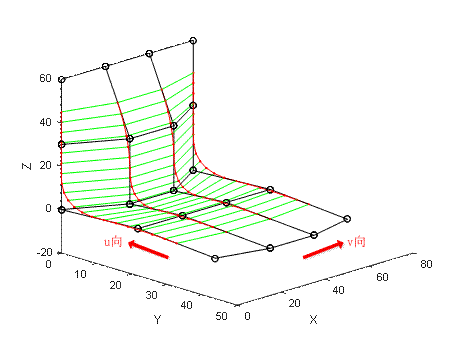
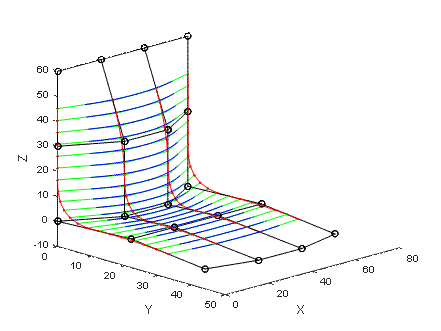
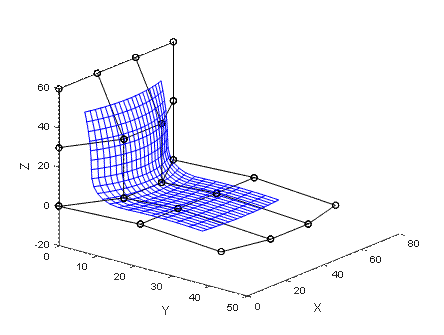
给定曲面的控制顶点并确定次数后,还需要根据不同类型的B样条曲面沿参数方向的节点矢量才能完全定义一张B样条曲面。要计算B样条曲面上的顶点坐标,首先沿一个参数方向如u向或v向,计算出该方向由控制顶点确定的B样条曲线,如下图中的红色曲线是沿u向生成的二次均匀B样条曲线,一共有四条。

之后将沿u向计算得到的B样条曲线上的点作为新的控制顶点,得到张量网格沿v向计算,得到的曲线就是B样条曲面上的,下图中绿色线段组成的就是沿v向的控制的顶点,蓝颜色的曲线是沿v向的二次均匀B样条曲线构成了一张二次均匀B样条曲面。关于B样条曲面实现的代码在这里可以下载。
参考文献:
[1] 施法中. 计算机辅助几何设计与非均匀有理B样条(修订版)[M]. 北京: 高等教育出版社, 2013.
B样条曲线曲面(附代码)的更多相关文章
- 分布式消息总线,基于.NET Socket Tcp的发布-订阅框架之离线支持,附代码下载
一.分布式消息总线以及基于Socket的实现 在前面的分享一个分布式消息总线,基于.NET Socket Tcp的发布-订阅框架,附代码下载一文之中给大家分享和介绍了一个极其简单也非常容易上的基于.N ...
- 分享5种风格的 jQuery 分页效果【附代码】
jPaginate 是一款非常精致的分页插件,提供了五种不同风格的分页效果,支持鼠标悬停翻页,快速分页功能.这款插件还提供了丰富的配置选项,你可以根据需要进行设置. 效果演示 源码下载 各个 ...
- Python进阶:函数式编程实例(附代码)
Python进阶:函数式编程实例(附代码) 上篇文章"几个小例子告诉你, 一行Python代码能干哪些事 -- 知乎专栏"中用到了一些列表解析.生成器.map.filter.lam ...
- c#万能视频播放器(附代码)
原文:c#万能视频播放器(附代码) c#万能视频播放器 本人之前很多的文章中均提到了使用libvlc为播放器内核制作的播放器,也许有些朋友对此感兴趣,于是我用c#写了一个调用libvlc api实现的 ...
- python德国信用评分卡建模(附代码AAA推荐)
欢迎关注博主主页,学习python视频资源,还有大量免费python经典文章 python信用评分卡建模视频系列教程(附代码) 博主录制 https://study.163.com/course/i ...
- 十图详解tensorflow数据读取机制(附代码)转知乎
十图详解tensorflow数据读取机制(附代码) - 何之源的文章 - 知乎 https://zhuanlan.zhihu.com/p/27238630
- 【转】- 从FM推演各深度CTR预估模型(附代码)
从FM推演各深度CTR预估模型(附代码) 2018年07月13日 15:04:34 阅读数:584 作者: 龙心尘 && 寒小阳 时间:2018年7月 出处: 龙心尘 寒小阳
- 数据挖掘领域十大经典算法之—C4.5算法(超详细附代码)
https://blog.csdn.net/fuqiuai/article/details/79456971 相关文章: 数据挖掘领域十大经典算法之—K-Means算法(超详细附代码) ...
- 【独家】阿里天池IJCAI17大赛第四名方案全解析(附代码)
[独家]阿里天池IJCAI17大赛第四名方案全解析(附代码) https://mp.weixin.qq.com/s?__biz=MzAxMzA2MDYxMw==&mid=2651560625& ...
- 球体的双目视觉定位(matlab,附代码)
球体的双目视觉定位(matlab,附代码) 标签(空格分隔): 机器视觉 引言 双目视觉定位是我们的一个课程设计,最近刚做完,拿出来与大家分享一下,实验的目的是在拍摄的照片中识别球体,并求出该球体到相 ...
随机推荐
- Microsoft Build 2015 汇总
简要概括(GitHub 完成约 45%): Visual Studio Code Preview(意料之外) Visual Studio 2015 RC Visual Studio 2013 Upda ...
- c++编译器对多态的实现原理总结
问题:定义一个空的类型,里面没有任何的成员变量或者成员函数,对这个类型进行 sizeof 运算,结果是? 结果是1,因为空类型的实例不包含任何信息,按道理 sizeof 计算之后结果是0,但是在声明任 ...
- 分享一下刚刚HP电话面试。。。。。。。。我估计我挂了,不过还是要来分享一下
面试官是个中国人,给我是全英文面试,总之是做HP的外包业务,说得很好的工作环境,里面都是一些老外在工作. 首先是要用英文介绍了下自己,我自己觉得自己也还是不错的吧,然后就说了一通(其实我好久没说英文了 ...
- PHP封装
封装 把成员方法和成员属性封装到类中,隐藏属性和方法实现的细节,通过public.protected.private等限定类成员的访问权限,数据被保护在内部,只通过被授权的成员方法才可以操作,尽 ...
- jQuery.grep()
什么是jQuery.grep()? jQuery.grep()是一个查找满足过滤函数的数组元素的函数.原始数组不受影响,返回值为数组. 用法介绍: 写法: jQuery.grep( array, fu ...
- iis7.0上发布mvc4.0网站
步骤如下: 1.右击需要发布的项目,在弹出的菜单中选择“发布...”选项 2.在“发布web”对话框中进行设置,配置文件名称默认为“配置文件1”可以修改为需要的名字,以便识别,也可以不改.发布方法选择 ...
- 使用Apache Server 的ab进行web请求压力测试
参考:http://www.cnblogs.com/spring3mvc/archive/2010/11/23/2414741.html 自己写代码经常是顺着逻辑写下去,写完后run一下,ok就玩完事 ...
- SQL Server 2016里的sys.dm_exec_input_buffer
在你的DBA职业里,你们谁有用过DBCC INPUTBUFFER命令,来获得已经提交到SQL Server特定会话的最后SQL语句?请举手!大家都用过! 我们都知道DBCC命令有点尴尬,因为你不能在T ...
- C#新手常犯的错误
虽然这篇post的标题是新手常犯的错误,实际上很多有经验的程序员也经常犯这些错误,我整理了一下,就当是笔记.1.遍历List的错误,比如如下代码: List<String> strList ...
- C#基础知识二之this关键字
this关键字 引用类的当前实例,包括继承而来的方法,通常可以省略. public class Person { public string Name { get; set; } public int ...
