机器学习进阶-svm支持向量机

支持向量机需要解决的问题：找出一条最好的决策边界将两种类型的点进行分开

这个时候我们需要考虑一个问题，在找到一条直线将两种点分开时，是否具有其他的约束条件，这里我们在满足找到一条决策边界时，同时使得距离边界最近的点到边界的距离最远，对于下图而言，我们可以看出右边的图比左边的图的分类效果要好，因为点到边界的距离较大，这样得到的决策边界具有较好的泛化能力。

SVR的求解过程

首先我们需要写出点到直线或者平面的距离，这里以平面为例

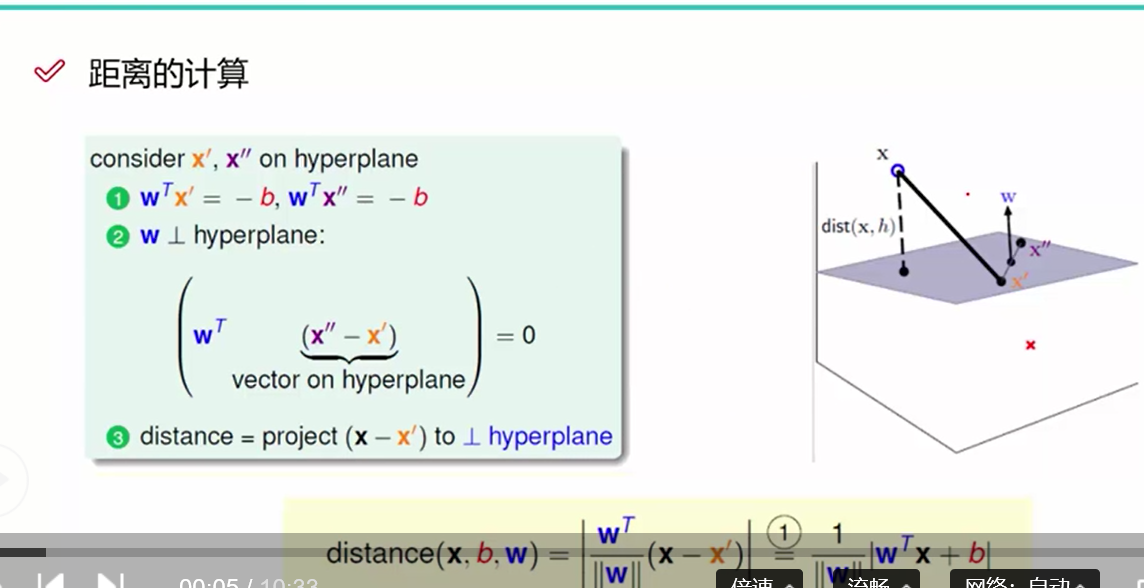
我们需要求得的是dist(x, h)即x点到平面的距离，我们x首先在平面上找到一个点x‘， a*b = |a|*|b|*cos(theta)

w^T*(x-x') / |w|  = (x-x') * cos(theta)  ----1 表示的是dist(x, h)

w表示的是法向量，因为x'为一个随机点，假设在平面上存在一个x',使得w^T*x' + b = 0 ---2

将上述的2式带入到1式中，对1式进行化解

dist(x, h) = 1/|w| * |w^T*x + b|

当为正例时yi等于1， 当为负例时yi等于-1

为了去除|w^T*x + b|的绝对值，当w^T*x + b > 0 时，yi>0, 当w^T*x + b < 0 时， yi<0, 我们可以将yi * (w^T*x + b) > 0 用来去除绝对值

dist(x, h) = 1/|w| * yi * (w^T*x + b)

优化目标：

找到一条直线w和b使得距离直线最近的点到直线的距离最大

即求得argmax(1/|w| * min(yi * (w^T + b)))

我们对yi * (w^T + b) 进行放缩操作，使得yi * (w ^ T + b) >= 1

那么min(yi * (w^T + b)) 的最小值即为1，上式化解为argmax(1/|w|) 求解这个的最大值，即求解1/2 *w**2 的最小值

这里我们构造拉格朗日乘子法，即求出1/2 * w**2的最大值，约束条件为-(yi*(w^T*x + b))

根据KTT对偶法，先求min max 等价于 max min

f(x) = max min (1/2 * w ** 2 - ai(yi*w^T*x +b - 1) )

先求解最小值，求解∂f(x) / ∂w

∂f(x) / ∂w  -= 0 -> w = Σai yi * θ(xi)

∂f(x) / ∂b = 0 -> 0 = Σai yi

将上述得到的结果带入原式中：

L(w, b, a)  = 1/2 *|w|^2 - Σai(yi*(w^T*x +b) - 1)

= 1/2 * |w|^2 - w^T*Σai*yi*x +b*Σaiyi -  Σai

= Σai - 1/2 * |w| ^ 2

= Σai - 1/2(Σai yi * θ(xi)^T*(Σai yi * θ(xi)

=Σai - 1/2Σaiyiajyi θ(xi)^T*θ(xj)^T

求解什么样的ai使得这个值最大

条件Σaiyi = 0 且拉格朗日法的限制即ai >= 0

对于求解极大值的问题，我们需要将极大值的求解转换为极小值的求解

目标函数 ：min 1/2Σaiyiajyi θ(xi)^T*θ(xj)^T - Σai

约束条件：Σaiyi = 0

ai >= 0

SVM求解实例

数据：3个点，其中正例X1(3, 3), X2(4, 3), 负例X3(1, 1)

求解：1/2Σaiyiajyi θ(xi)^T*θ(xj)^T - Σai   的最小值

约束条件 a1 + a2 - a3 = 0

ai >= 0, i = 1, 2, 3

原式： 1/2ΣΣaiajyiyj(xi*xj) - Σai : 将数据带入

1/2(18*a1^2 + 25*a2^2 +2*a3^2 +42*a1*a2 - 12*a1*a2 - 14a2*a3) - a1 - a2 - a3

由于: a1 + a2 = 0 化简可得： 4a1^2 + 13/2*a2^2 + 10*a1*a2 - 2a1 - 2a2

求解上述式子的最小值，对a1进行求导使得偏导等于0，解得a1 = 1.5， a2 = -1 不满足约束条件ai >= 0 ，

因此解在边界上，即a1 = 0 时  a2 = -2/13 代入原式 = -0.153 不满足约束条件

a2 = 0时，a1 = 0.25 代入原式=-0.25 满足约束条件

将a结果带入到w =  Σai yi * θ(xi)， 解得w = (1/2, 1/2)

b = 1 -  w^T * x = 1 - Σai yi * (xi*xj) 选择第一个x1点带入，

= 1 - (1/4 * 1 * 18 + 1/4 * (-1) * 6 ) = -2

平面方程为：0.5x1 +0.5x2 - 2 = 0

从上述的求解我们可以知道，支持向量机表示的是ai不等于0的店，不是支持向量机其他的点都等于0