[Alg::DP] Square Subsequence

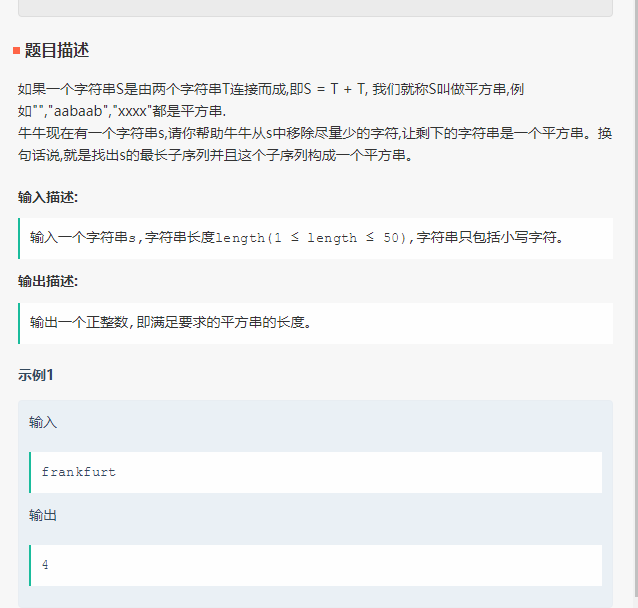
题目如下：

#include <iostream>
#include <string>
#include <vector>

using namespace std;

// use this struct to store square subsequence, 4 positions and 1 length
struct SqSb {
    // take square subsequence as two subsquence s0 and s1
    int s00; // the position of s0's first char
    int s01; // the position of s0's last char
    int s10;
    int s11;
    int len;
    SqSb() {
        s00 = s01 = s10 = s11 = 0;
        len = 0;
    }
    SqSb(int t00, int t01, int t10, int t11, int length) {
        s00 = t00;
        s01 = t01;
        s10 = t10;
        s11 = t11;
        len = length;
    }
};

int maxSqSubLen(const string & str) {

    int strLen = str.size();

    // corner cases
    if (strLen < 1) return 0;

    if (strLen == 2) {
        if (str[0] == str[1]) return 2;
        else return 0;
    }
    // corner cases end

    // dp[i] stores the square subsequence of length (i + 1) * 2
    vector<vector<SqSb> > dp;
    // dp1 == dp[0] is the initial data
    vector<SqSb> dp1;

    for (int i = 0; i < strLen - 1; ++i) {
        char ich = str[i];
        for (int j = i + 1; j < strLen; ++j) {
            if (ich == str[j]) {
                SqSb s(i, i, j, j, 2);
                dp1.push_back(s);
            }
        }
    }

    // there is no duplicate char in this string return
    if (dp1.empty()) return 0;

    dp.push_back(dp1);

    for (int l = 2; l <= strLen/2; ++l) {
        vector<SqSb> dpl;
        for (int i = 0; i < dp[l - 2].size(); ++i) {
            SqSb si = dp[l - 2][i];
            for (int j = 0; j < dp1.size(); ++j) {
                SqSb sj = dp1[j];
                if (sj.s00 > si.s01 && sj.s00 < si.s10
                && sj.s10 > si.s11) {
                    SqSb s(si.s00, sj.s00, si.s10, sj.s10, l * 2);
                    dpl.push_back(s);
                }
            }
        }
        if (dpl.empty()) return (l - 1) * 2;
        dp.push_back(dpl);
    }

    return strLen/2 * 2;
}

int main(int argc, char **argv) {

    cout << maxSqSubLen(string(argv[1])) << endl;

    return 0;
}

参考的是 stackoverflow 的一个提问：https://stackoverflow.com/questions/10000226/square-subsequence

题目不难，知道DP的整体流程，但是分析问题的能力差了一点。