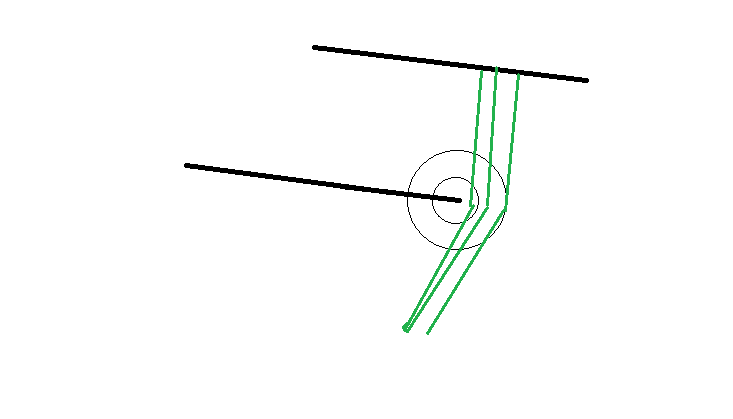
历史上,物理学是用波动说来解释光的衍射现象。但用微粒说结合广义相对论同样可以做到。

把光看作粒子，当经过障碍物边缘时，由于广义相对论效应，边缘附近的空间被弯曲，使得不同路径的平行光发生偏转，落在障碍物后面的成像屏上。

用光的微粒说和广义相对论来解释衍射现象 Explanation of Diffraction Phenomenon by Particle Theory of Light and General Relativity的更多相关文章

  1. 量子力学与广义相对论的统一——用广义相对论解释海森堡测不准原理 Unification of Quantum Mechanics and General Relativity: Explaining Heisenberg Uncertainty Principle with General Relativity

    从海森堡测不准原理的实验开始: 从实验中可以看到,当有光源测定路线,且双孔打开的时候,接收板原波谷处变成了波峰. 对此,广义相对论的解释是:此时电子经过双孔后的轨迹发生了变化.双孔周围的空间弯曲度被光 ...

  2. LIGO找到首个超越广义相对论的证据？

    转自 麻省理工科技评论 原文 LIGO找到首个超越广义相对论的证据? 1915年,爱因斯坦根据简单的原理提出广义相对论,极大地改变了人们的时空观.广义相对论不仅解释了牛顿理论无法解释的现象,还做出许多 ...

  3. SharpGL学习笔记(九) OpenGL的光照模型, 术语解释

    在3D场景中,每个像素最终显示出来的颜色都是经过大量计算而得到的,其中一些计算是依赖于场景中的光照以及场景中物体对光线的反射和吸收情况. 例如,对于一个红色的物体, 在白色光(白光是红光,绿光和蓝光等 ...

  4. 由浅入深学习PBR的原理和实现

    目录 一. 前言 1.1 本文动机 1.2 PBR知识体系 1.3 本文内容及特点 二. 初阶:PBR基本认知和应用 2.1 PBR的基本介绍 2.1.1 PBR概念 2.1.2 与物理渲染的差别 2 ...

  5. 机器学习中模型泛化能力和过拟合现象(overfitting)的矛盾、以及其主要缓解方法正则化技术原理初探

    1. 偏差与方差 - 机器学习算法泛化性能分析 在一个项目中,我们通过设计和训练得到了一个model,该model的泛化可能很好,也可能不尽如人意,其背后的决定因素是什么呢?或者说我们可以从哪些方面去 ...

  6. 看见上帝的 10 个公式……

    原文 Top Ten Greatest Equations Ever 本文内容 No.1 麦克斯韦方程组 No.2 欧拉方程 No.3 牛顿第二定律 No.4 毕达哥拉斯定理 No.5 薛定谔方程 N ...

  7. <<Differential Geometry of Curves and Surfaces>>笔记

    <Differential Geometry of Curves and Surfaces> by Manfredo P. do Carmo real line Rinterval I== ...

  8. lecture12-玻尔兹曼机和受限玻尔兹曼机

    这是Hinton的第12课,结合前一课可以知道RBM是来自BM,而BM是来自Hopfield的,因为水平有限,是直译的,虽然有时候会看不懂,但是好歹不会曲解原来的本意,看的话:1.先看ppt:2.通读 ...

  9. sentence patterns

    第四部分     推理题 1.世界上每个角落的每个人都有立场,都有背景,都有推理性,能推理出一个人语言的真意,才成就了真正的推理能力: 2.换言之,如果你能通过一个人的说话推理出其身份职业,你的推理能 ...

随机推荐

  1. [SoapUI] 在SoapUI中通过Groovy脚本执行window命令杀掉进程

    //杀Excel进程 String line def p = "taskkill /F /IM EXCEL.exe".execute() def bri = new Buffere ...

  2. IOS代码片段

    2017-08-03 获取应用程序委托FKAppDelegate* appDelegate = [UIApplication shareApplication].delegate 2017-08-03 ...

  3. js--延时消失的菜单--（笔记）

    html:有4个li,li下分别有一个span <script>   window.onload=function(){    var aLi=document.getElementsBy ...

  4. nginx xxx.conf

    server { listen 80 ; server_name xxx.test.cn localhost 127.0.0.1 115.29.96.222; access_log /var/log/ ...

  5. eclipse构建maven的web项目（转载）

    eclipse构建maven的web项目 分类: java opensource2013-12-25 16:22 43人阅读 评论(0) 收藏 举报 maven框架webappwebeclipse 使 ...

  6. spring学习 八 面向切面编程(AOP)概述

    注:本文大部分参考   --------------------- 本文来自 -望远- 的CSDN 博客 ,全文地址请点击:https://blog.csdn.net/yanquan345/artic ...

  7. 819. Most Common Word

    static int wing=[]() { std::ios::sync_with_stdio(false); cin.tie(NULL); ; }(); class Solution { publ ...

  8. 2019.01.22 bzoj3333: 排队计划（逆序对+线段树）

    传送门 题意简述:给出一个序列,支持把ppp~nnn中所有小于等于apa_pap​的'扯出来排序之后再放回去,要求动态维护全局逆序对. 思路:我们令fif_ifi​表示第iii个位置之后比它大的数的个 ...

  9. 2019.01.13 bzoj1146: [CTSC2008]网络管理Network（整体二分+树剖）

    传送门 题意简述:给一棵树,支持单点修改,询问路径上两点间第kkk大值. 思路: 读懂题之后立马可以想到序列上带修区间kkk大数的整体二分做法,就是用一个bitbitbit来支持查值. 那么这个题把树 ...

  10. 注解Demo

    1.创建注解类 2.在测试实体类中使用注解 3.构建注解解析类 4.执行注解解析方法