c语言求平面上2个坐标点的直线距离、求俩坐标直线距离作为半径的圆的面积、递归、菲波那次数列、explode

 #include <stdio.h>
 #include <math.h>
 #include <string.h>

 char explode( char * str , char symbol );

 double distance ( int x1 , int y1 , int x2 , int y2 );                    // 求平面上2个坐标点的直线距离
 double circle_area( double radius );                                    // 求圆面积。 radius 半径
 double two_point_cacl_circle_area ( int x1 , int y1 , int x2 , int y2 );// 从两点坐标，求圆的面积

 // 阶乘，递归方式实现。
 int jiecheng( int N );

 // 递归方式，求2数的最大公约数
 int digui_gongyueshu( int a , int b );
 // 菲波那次数列
 int fibonacci( int N );

 int main( int argc , char ** argv ){
     char * str = "4;5;6;18;26;31;42;57;66;67;68;69;70;71;72;73;74;75;76;77;78;79;80;81;82;83;84;85;86;89;90;91;93;94;95;96;97;98;99;100;101;102;103;104;105;1051;1052;1310;1023;1041;1203;1256;1259;1260;1270;1210;1209;1279;1282;1278;1211;1276;1275;1240;1236;1235;1234;1239;1281;1028;1026;1231;1232;1277;1042;1050;1019;1267;1266;1268;1295;1265;1264;1258;1289;1219;1218;1217;1216;1016;1252;1251;1250;1249;1245;1244;1215;1243;1242;1302;1255;1287;1241;1253;1230;1271;1272;1054;1283;1284;1285;1286;";
     char * result = "";
     char list = {};
     int x1 =  , y1 =  , x2 =  , y2 = ; // 2个坐标 

     printf( "\n求阶乘的结果是：%d \n" , jiecheng(  ) );

     printf( "\n平面上2个坐标x1( %d , %d ) , x2(  %d , %d )，的直线距离是：%f \n" , x1 , y1 , x2 , y2 ,  distance( x1 , y1 , x2 , y2 ) );

     printf( "\n平面上2个坐标x1( %d , %d ) , x2(  %d , %d )，的直线距离作为圆的半径时，这个圆的面积是：%f \n" , x1 , y1 , x2 , y2 ,  two_point_cacl_circle_area( x1 , y1 , x2 , y2 ) );

     printf( "\n 8和5 的最大公约数是: %d " , digui_gongyueshu(   ,  ) );
     printf( "\n 8和15 的最大公约数是: %d \n" , digui_gongyueshu(   ,  ) );

     int i = ;
     for( ; i <=  ; ++i ){
         printf( "\n %d 的菲波那次数列 值是: %d " , i , fibonacci( i ) );
     } 

     //printf( "%s \n" , str );
     return ;
 }

 char explode( char * str , char symbol ){
     char list = {};
     int i =  , j = ;
     int len = strlen( str ) ;
     // int len = sizeof( list ) / sizeof( int ); // 如果是int,float,double型, 通过sizeof()来计算list的长度

     /*
     for( ; i < len ; ++i ){
         if( str[ i ] != symbol ){
             list[ j ] += str[i];
         }
         else{
             ++ j;
         }
     }
     */

     return list;
 }

 // 通过画勾股定理直角三角形 ，求平面上2个坐标点之间的巨鹿
 double distance ( int x1 , int y1 , int x2 , int y2 )  {
     int x =  , y = ;
     double res = 0.0;

     x = abs( x2 - x1 ); // 直角三角形的 勾
     y = abs( y2 - y1 ); // 直角三角形的 股 

     res = sqrt( x * x + y * y ) ; // 勾股定理 求 斜线
     return res;
 }

 // 求圆面积。 radius 半径
 double circle_area( double radius ){
     double pi = 3.1416 ;
     return pi * radius * radius;
 }

 // 从两点坐标，求圆的面积
 double two_point_cacl_circle_area ( int x1 , int y1 , int x2 , int y2 ){
     return circle_area( distance( x1 , y1 , x2 ,  y2 ) );
 }

 // 阶乘，递归方式实现。
 int jiecheng( int N ){
     int res =  ;

     // 先写1个，参数最小的情况的返回值
     if( N ==  ){
         res = ;
     }
     // 再写1个递归调用的情况。
     else{
         res = N * jiecheng( N -  );
     }
     printf( "%d阶乘的结果：%d \n" , N , res );
     // 完成递归。
     return res;

     /*
         我们从数学上严格证明一下factorial函数的正确性。
         刚才说了，factorial(n)的正确性依赖于factorial(n-1)的正确性，
         只要后者正确，在后者的结果上乘个n返回这一步显然也没有疑问，那么我们的函数实现就是正确的。

         因此要证明factorial(n)的正确性就是要证明factorial(n-1)的正确性，
         同理，要证明factorial(n-1)的正确性就是要证明factorial(n-2)的正确性，

         依此类推下去，最后是：要证明factorial(1)的正确性就是要证明factorial(0)的正确性。

         而factorial(0)的正确性不依赖于别的函数，它就是程序中的一个小的分支return 1;，
         这个1是我们根据阶乘的定义写的，肯定是正确的，因此factorial(1)也正确，
         因此factorial(2)也正确，
         依此类推，最后factorial(n)也是正确的。

         其实这就是中学时讲的数学归纳法（Mathematical Induction），
         用数学归纳法来证明只需要证明两点：Base Case正确，递推关系正确。
     */
 }

 // 递归方式，求2数的最大公约数
 int digui_gongyueshu( int a , int b ){
     int res =  ;
     if( a % b ==  ){
         res = b;
     }
     else{
         res = digui_gongyueshu( b , a % b );
     }
     return res;

     /*
         1、编写递归函数求两个正整数a和b的最大公约数（GCD，Greatest Common Divisor），使用Euclid算法：

           1. 如果a除以b能整除，则最大公约数是b。
           2.否则，最大公约数等于b和a%b的最大公约数。

         Euclid算法是很容易证明的，请读者自己证明一下为什么这么算就能算出最大公约数。
     */
 }

 // 菲波那次数列
 int fibonacci( int N ){
     int res =  ;

     if( N ==  || N ==  ){
         res = ;
     }
     else{
         res = fibonacci( N -  ) + fibonacci( N -  );
     }
     return res;
 }

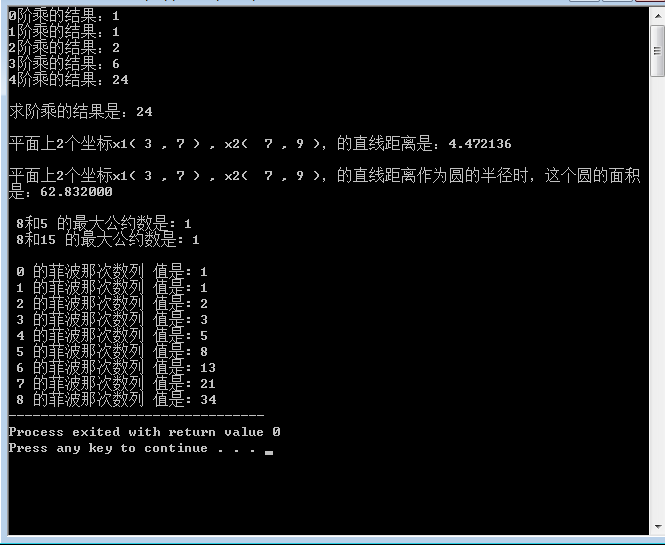
c语言求平面上2个坐标点的直线距离、求俩坐标直线距离作为半径的圆的面积、递归、菲波那次数列、explode