matlab-单位圆内射线数次反射

转载自 https://zhidao.baidu.com/question/2268408219692883828.html

先贴代码和放图，然后我再做出一点解释（其实只是觉得这个思路好厉害，所以想保存下来）

%% Draw circle
[cx, cy] = pol2cart(linspace(0, 2*pi, 100), 1);
plot(cx, cy, 'r')
axis equal
hold on
 
%% Init particle - You can modify this
[px, py] = pol2cart(rand()*2*pi, rand());
p = [px; py];
plot(px, py, 'o')
v = rand(2, 1);
v = v/norm(v);
 
%%
R = @(t)[cos(t) -sin(t); sin(t) cos(t)];
P = p;
O = [0; 0];
 
t = fmincon(@(t)abs(norm(p+t*v) - 1), -1, 1, 0);
p = p+t*v;
for i = 1:10    % iterate 10 times
    p = p + 2*(O - p)'*v*v;
    P = [P p];
    t = atan2(p(2), p(1));
    v = R(t) * diag([-1 1]) * R(-t) * v;
end
plot(P(1,:), P(2,:))

　

　

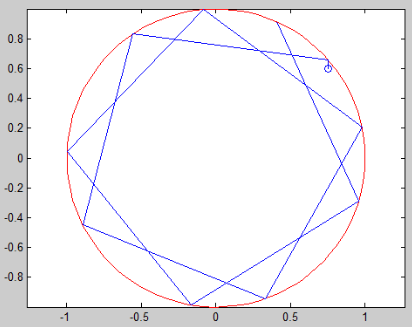
这个思路是利用向量来做的。v就是这个方向的单位向量。p就是向量原点。

(O - p)'*v*v; 得到的是 这个向量

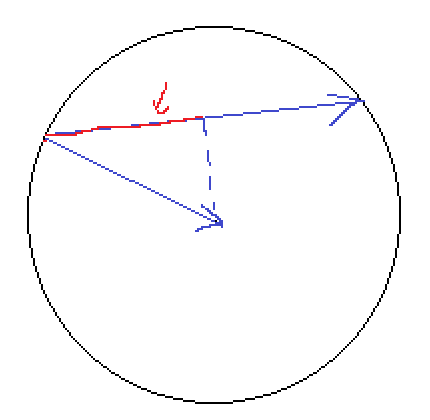
R是 光学谐振腔的的凹型镜面的反射矩阵

v = R(t) * diag([-1 1]) * R(-t) * v; 用的就是激光原理里面的这部分内容

之后就是一步一步的迭代了