洛谷P1477 假面舞会

坑死了......

题意：给你个有向图，你需要把点分成k种，满足每条边都是分层的(从i种点连向i + 1种点，从k连向1)。

要确保每种点至少有一个。

求k的最大值，最小值。

n <= 1e5, m <= 1e6, k >= 3。

解：

首先可以发现，如果存在一个环，那么k一定是环长的约数。

然后我们把所有环长的gcd求出来就行了......

考虑这几种情况：

情况①：

这启示我们要拓扑排序或建反向边。鉴于这个图可能有环，我们建长度为-1的反向边。

情况②：

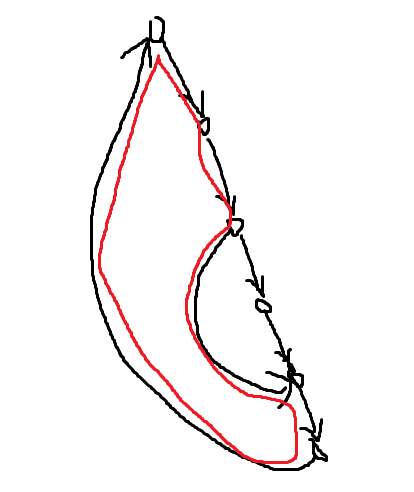
这个红色的环怎么办？

事实上只要别的两个环满足了，这个组合起来的环也能够被满足(意会一下)。

情况⑨：

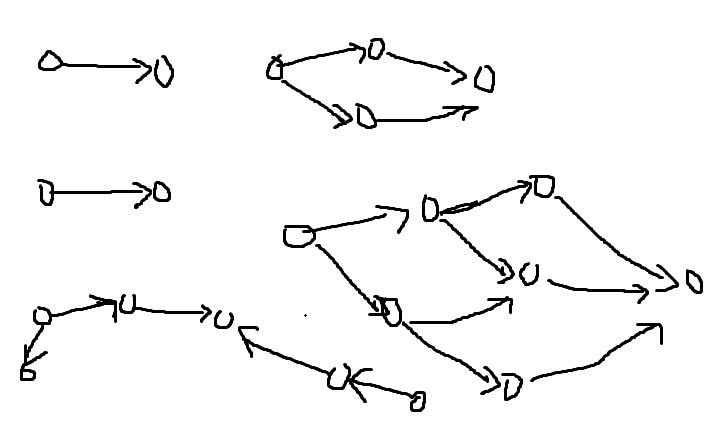
这启示我们在无环/环长全部为0的时候进行特殊处理。

然后写代码的时候出了一堆错......50分暴力发现比正解还难打，不会写......

 #include <cstdio>
 #include <algorithm>
 #include <cstring>

 const int N = , M = , INF = 0x3f3f3f3f;

 struct Edge {
     int nex, v, len;
 }edge[M << ]; int top = ;

 int e[N], m, n, vis[N], small, large, fd, g;

 int gcd(int a, int b) {
     if(!b) {
         return a;
     }
     return gcd(b, a % b);
 }

 inline void add(int x, int y, int z) {
     top++;
     edge[top].nex = e[x];
     edge[top].len = z;
     edge[top].v = y;
     e[x] = top;
     return;
 }

 void DFS(int x, int in_e) { // error : in_edge space
     small = std::min(small, vis[x]);
     large = std::max(large, vis[x]);
     //printf("vis[%d] = %d \n", x, vis[x]);
     for(int i = e[x]; i; i = edge[i].nex) {
         if((i ^ ) == in_e) {
             continue;
         }
         int y = edge[i].v;
         if(vis[y] == INF) {
             vis[y] = edge[i].len + vis[x];
             DFS(y, i);
         }
         else {
             int cir = abs(edge[i].len + vis[x] - vis[y]); // error : abs(vis[x] - vis[y]) + 1
             //printf(">_<  >>>  [%d]%d [%d]%d \n", x, vis[x], y, vis[y]);
             //printf("cir = %d \n", cir);
             g = gcd(g, cir);
             fd = ;
         }
     }
     return;
 }

 int main() {

     scanf("%d%d", &n, &m);
     for(int i = , x, y; i <= m; i++) {
         scanf("%d%d", &x, &y);
         add(x, y, );
         add(y, x, -);
     }
     memset(vis, 0x3f, sizeof(vis));
     int lenth = ;
     for(int i = ; i <= n; i++) {
         if(vis[i] == INF) {
             large = small = ;
             vis[i] = ;
             DFS(i, );
             lenth += large - small + ;
         }
     }

     //printf("fd = %d \n", fd);

     if(!fd || !g) { // error : !g space
         if(n <=  || lenth <= ) { // error : lenth <= 2 space
             printf("-1 -1");
         }
         else {
             printf("%d 3", lenth);
         }
         return ;
     }
     if(g < ) {
         printf("-1 -1");
     }
     else {
         printf("%d ", g);
         for(int i = ; i <= g; i++) {
             if(g % i == ) {
                 printf("%d", i);
                 break;
             }
         }
     }

     return ;
 }

AC代码

太毒瘤了......