Tarjan总结（缩点+割点(边)+双联通+LCA+相关模板）
Tarjan求强连通分量
先来一波定义
强连通：有向图中A点可以到达B点，B点可以到达A点，则称为强连通
强连通分量：有向图的一个子图中，任意两个点可以相互到达，则称当前子图为图的强连通分量
强连通图： 如果在一个有向图中，每两个点都强连通，我们就叫这个图叫强连通图。
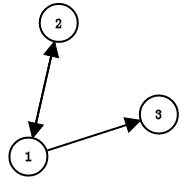(一张十分简洁的图）
如图，图中{1,2}就是一个强连通，也是这个图中的一个强连通分量
求强连通分量的算法有三种：
Kosaraju算法，Tarjan算法，Gabow算法(然而我只会用Tarjan求)
这里就稍微介绍一下tarjan求强连通分量
首先要明白几个概念：
时间戳(dfn)：dfn就是在搜索中某一节点被遍历到的次序号，
节点能追溯到的最早的栈中节点的时间戳(low)：low就是某一节点在栈中能追溯到的最早的父亲节点的时间戳。
Tarjan算法就是基于深度优先搜索的算法：把没有标记过时间戳的点放入栈中，然后以它为根进行搜索，搜索完后回溯更新low，保证low一定是最小的，如果发现low[u] == dfn[u]，就把u上面的全部弹出栈内，这些点就构成了强连通分量，而这个u就是一个关键节点：从这个节点能够到达其强连通分量中的其他节点，但是没有其他属于这个强连通分量以外的点能够到达这个点，所以这个点的low[u]值维护完了之后还是和dfn[u]的值一样
这样描述还是太抽象了点，还是走一遍流程吧
cnt为计数器
一张经典的图：
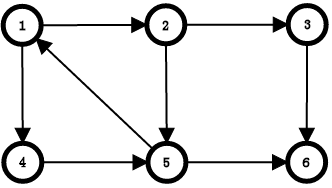
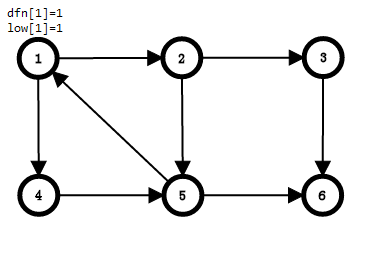
搜到1，1入栈，dfn[1] = low[1] = ++cnt，栈内元素：1
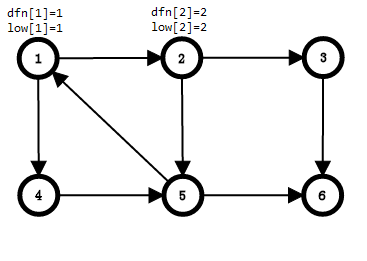
搜到2，2没被搜过，2入栈，dfn[2] = low[2] = ++cnt，栈内元素：1，2
搜到3，3没被搜过，3入栈，dfn[3] = low[3] = ++cnt，站内元素：1，2，3
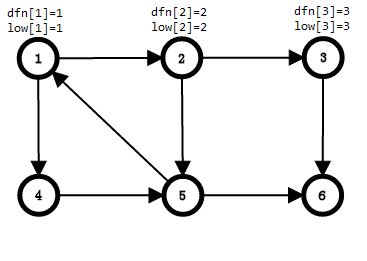
搜到6，6没被搜过，6入栈，dfn[6] = low[6] = ++cnt，站内元素：1，2，3，6
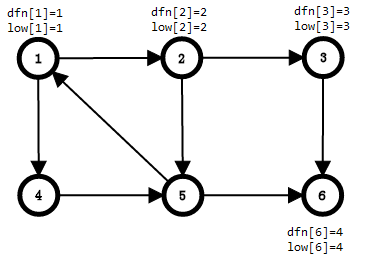
6没有出边，此时
发现low[6] == dfn[6]，把6弹出，6为强连通分量
回溯到3，发现low[3] == dfn[3]，把3弹出，3为强连通分量
回溯到2，发现2还可以到5，搜索5
搜到5，5没被搜过，5入栈，dfn[5] = low[5] = ++cnt，栈内元素1，2，5
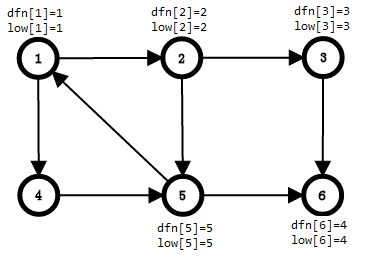
搜到1，发现1被搜过了且在栈内，因为low是节点能追溯到的最早的栈中节点的时间戳，我们要保证low最小，所以我们要更新low[5] = min(low[5],dfn[1]) = 1
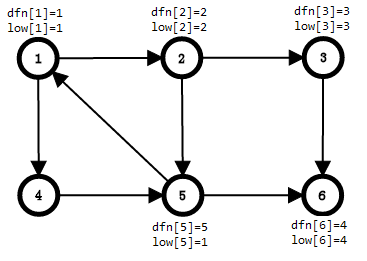
再搜到6，6被搜过但不再栈内，不管
没有其他边了，回溯，回溯到2，因为low要最小，而后面的low值要<=当前的，所以用后面的更新当前的，更新2的值low[2] = min(low[2],low[5])
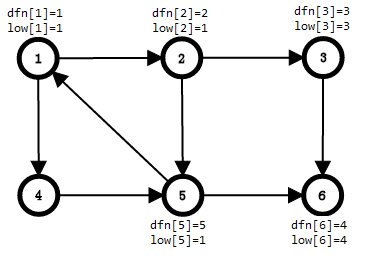
回溯到1
继续搜，搜到4，4没有被搜过，4入栈，栈内元素：1，2，5，4
再搜到5，发现5在栈内，就更新low[4]，low[4] = min(low[4],dfn[5]) = 5
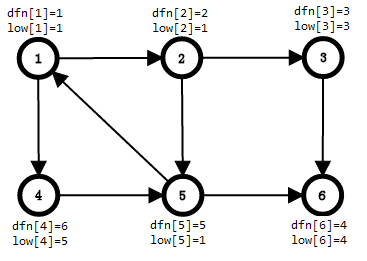
没有其他的边了，然后回溯，回溯到1
发现dfn[1] == low[1]
于是乎我们将所有1上面的元素及1弹栈，得到一个强连通分量1，2，5，4
于是这个图中就有3个强连通分量
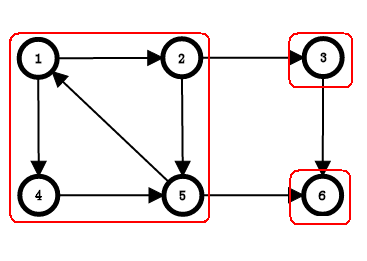
代码：
//vis[i]表示i是否在栈中
//sum表示是连通块个数
//size[i]表示第i个连通块内的元素个数
//bel[i]表示i属于哪个连通块belong也可以理解为color
stack<int>s;
void tarjan(int u) {
dfn[u] = low[u] = ++ cnt;
vis[u] = ;//标记是否在栈内
s.push(u);
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[v]) low[u] = min(low[u],dfn[v]);
}
if(low[u] == dfn[u]) {
;sum ++;
while(x != u) {//x枚举栈内元素
x = s.top(),s.pop();
vis[x] = ,bel[x] = sum;
size[sum] ++;
}
}
}
但因为并不一定所有的点都相连，如
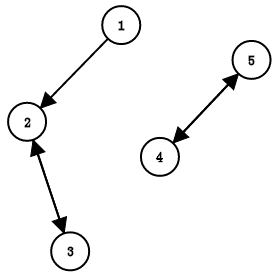
所以我们遍历的时候要：
; i <= n; ++ i) if(!dfn[i]) tarjan(i);
例题：
很多题都会用到缩点的思想，所以这里先给出两个练手的
//求强连通分量的个数是不是等于1
#include <bits/stdc++.h>
using namespace std;
;
int n,m,num,cnt,sum;
int dfn[N],low[N],head[N],bel[N];
bool vis[N];
struct node {
int v,nx;
}e[N];
template<class T>inline void read(T &x) {
x = ;;char ch =getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
stack<int>s;
void tarjan(int u) {
dfn[u] = low[u] = ++cnt;
vis[u] = ;
s.push(u);
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[u]) low[u] = min(dfn[v],low[u]);
}
if(dfn[u] == low[u]) {
;sum ++;
while(u != x) {
x = s.top(),s.pop();
vis[x] = ,bel[x] = sum;
}
}
}
int main() {
while(scanf("%d%d",&n,&m)) {
&& m == ) break;
memset(head,-,sizeof(head));
memset(vis,,sizeof(vis));
memset(dfn,,sizeof(dfn));
memset(low,,sizeof(low));
memset(bel,,sizeof(bel));
memset(e,,sizeof(e));
num = sum = cnt = ;
,x,y; i <= m; ++ i) read(x),read(y),add(x,y);
; i <= n; ++ i) if(!dfn[i]) tarjan(i);
) printf("Yes\n");
else printf("No\n");
}
;
}
HDU 1269
P2863 [USACO06JAN]牛的舞会The Cow Prom
//求联通块内的元素个数是否大于1
#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>
using namespace std;
const int N = 1e6;
int n,m,num,cnt,tot,sum,ans;
int a[N],b[N],head[N],size[N],bel[N],dfn[N],low[N];
bool vis[N];
stack<int>s;
struct node {
int v,nx;
}e[N];
template<class T>inline void read(T &x) {
x = ;;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
void tarjan(int u) {
dfn[u] = low[u] = ++cnt;
vis[u] = ;
s.push(u);
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[u]) low[u] = min(dfn[v],low[u]);
}
if(dfn[u] == low[u]) {
int x;sum ++;
while(u != x) {
x = s.top(),s.pop();
vis[x] = ,bel[x] = sum;
size[sum] ++;
}
}
}
int main() {
memset(head,-,sizeof(head));
read(n),read(m);
,x,y; i <= m; i ++) {
read(x),read(y);
add(x,y);
}
; i <= n; i ++) if(!dfn[i]) tarjan(i);
; i <= sum; i ++) {
)
ans ++;
}
printf("%d",ans);
;
}
P2863
Tarjan缩点
个人觉得分不分开讲一个样，缩点就是在上面的内容之后附加一个操作
其实缩点可以看做是一种解题方法罢
简单说，就是把一个强连通分量里的点做为一个点处理
也就是把bel数组里的元素当成点看就好了
假设我们有一张图长这个样：
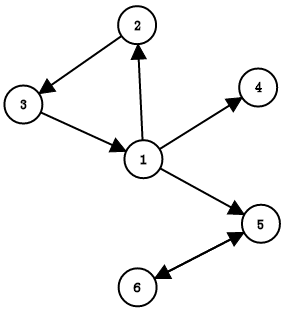
那我们操作的时候就可以脑补成这样
---->
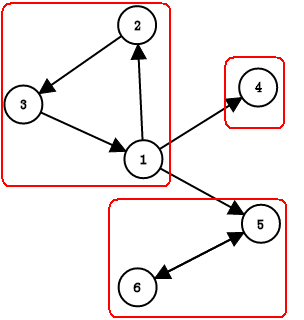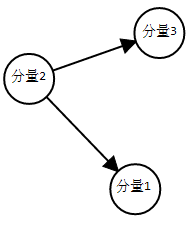
emmmm.....一般题目都会说如果相互到达就balabalbala
具体代码呢，就是枚举某个点的连边连向的点，如果在同一分量里，就不予处理，否则就按题目要求处理
; i <= n; ++ i)
for(int j = head[i]; ~j; j = e[j].nx) {
int v = e[j].v;
if(bel[i] != bel[v]) /*.code.*/
}
异常的容易
那就直接看题目吧：
//求入度为0的点的个数
#include <bits/stdc++.h>
using namespace std;
;
;
int n,m,cnt,sum,ans,num;
int head[N],dfn[N],low[N],bel[N],in[N];
bool vis[N];
struct node {
int v,nx;
}e[M];
template<class T>inline void read(T &x) {
x = ;;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
stack<int>s;
void tarjan(int u) {
dfn[u] = low[u] = ++cnt;
vis[u] = ;
s.push(u);
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[v]) low[u] = min(low[u],dfn[v]);
}
if(low[u] == dfn[u]) {
int x;sum ++;
while(x != u) {
x = s.top(),s.pop();
vis[x] = ,bel[x] = sum;
}
}
}
int main() {
memset(head,-,sizeof(head));
read(n),read(m);
,x,y; i <= m; ++ i) {
read(x),read(y);
if(x == y) continue;
add(x,y);
}
; i <= n; ++ i) if(!dfn[i]) tarjan(i);
; i <= n; ++ i)
for(int j = head[i]; ~j; j = e[j].nx) {
int v = e[j].v;
if(bel[i] != bel[v]) in[bel[v]] ++;
}
// for(int i = 1; i <= n; ++ i) cout<<in[bel[i]]<<" ";
; i <= sum; ++ i) if(!in[i]) ans ++;
cout<<ans;
;
}
P2002
//找出度为0的点
//代码历史久远，以2002为准
#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>
using namespace std;
const int N = 1e6;
int n,m,tot,sum,ans,cnt,num;
int a[N],b[N],head[N],dfn[N],low[N],size[N],bel[N];
bool vis[N],mark[N];
struct node {
int v,nx;
}e[N];
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
stack<int>s;
void tarjan(int u) {
dfn[u] = low[u] = ++cnt;
vis[u] = ;
s.push(u);
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[v]) low[u] = min(low[u],dfn[v]);
}
if(dfn[u] == low[u]) {
int x;sum ++;
while(u != x) {
x = s.top(),s.pop();
vis[x] = ,bel[x] = sum;
size[sum] ++;
}
}
}
int main() {
memset(head,-,sizeof(head));
scanf("%d%d",&n,&m);
; i <= m; i ++) {
scanf("%d%d",&a[i],&b[i]);
add(a[i],b[i]);
}
; i <= n; i ++) if(!dfn[i]) tarjan(i);
; i <= m; i ++) ;
; i <= sum; i ++) if(!mark[i]) ans = size[i],tot++;
) printf("%d",ans);
");
;
}
P2341
/*
tarjan
第一问求所有联通块的块中最小值之和，开一个mn数组在tarjan中记录
根据乘法原理，第二问求所有块中 价值=最小值的个数 的乘积
*/
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e6;
;
ll n,m,num,cnt,sum,ans,ans1 = ;
ll mn[N],dfn[N],low[N],bel[N],size[N],a[N],head[N];
bool vis[N];
struct node {
ll v,nx;
}e[N];
template<class T>inline void read(T &x) {
x = ;ll f = ;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return;
}
inline void add(ll u,ll v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
stack<ll>s;
void tarjan(ll u) {
dfn[u] = low[u] = ++ cnt;
vis[u] = ;
s.push(u);
for(ll i = head[u]; ~i; i = e[i].nx) {
ll v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[v]) low[u] = min(low[u],dfn[v]);
}
if(low[u] == dfn[u]) {
ll x=-;sum ++;
while(x != u) {
x = s.top(),s.pop();
bel[x] = sum,vis[x] = ;
if(mn[sum] == a[x]) size[sum] ++;
else if(mn[sum] > a[x]) {
mn[sum] = a[x];
size[sum] = ;
}
}
}
}
int main() {
memset(head,-,sizeof(head));
read(n);
; i <= n; ++ i) mn[i] = 0x7fffffff;
; i <= n; ++ i) read(a[i]);
read(m);
,x,y; i <= m; ++ i) read(x),read(y),add(x,y);
; i <= n; ++ i) if(!dfn[i]) tarjan(i);
; i <= sum; ++ i) {
ans += mn[i];
ans1 = ans1 * size[i] % mod;
}
cout<<ans<<" "<<ans1;
;
}
P2194
P2746 [USACO5.3]校园网Network of Schools
//同样历史久远
//1.求缩点后入度为0 的点的个数
//2.求入度为0的点数与出度为0的点的较大值
#include <bits/stdc++.h>
using namespace std;
;
int n,m,num,sum,cnt,j,ans,ans1;
int dfn[N],low[N],size[N],bel[N],x,kk[N][N],head[N];
bool vis[N],mark[N],mark1[N];
struct node {
int v,nx;
}e[N];
template<class T>inline void read(T &x) {
x = ;;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return;
}
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
stack<int>s;
void tarjan(int u) {
dfn[u] = low[u] = ++cnt;
s.push(u);
vis[u] = ;
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[v]) low[u] = min(low[u],dfn[v]);
}
if(dfn[u] == low[u]) {
int x;sum ++;
while(x != u) {
x = s.top(),s.pop();
vis[x] = ,bel[x] = sum;
size[sum] ++;
}
}
}
int main() {
memset(head,-,sizeof(head));
read(n);
; i <= n; ++ i) {
; j <= n + ; ++ j) {
read(x);
) break;
kk[i][j] = x;
add(i,x);
}
}
; i <= n; ++ i) if(!dfn[i]) tarjan(i);
; i <= n; ++ i) {
; kk[i][j] != ; j ++) ,mark1[bel[i]] = ;
}
) {
printf("%d\n0",sum);
;
}
; i <= sum; ++ i) {
if(!mark[i]) ans ++;
if(!mark1[i]) ans1 ++;
}
printf("%d\n%d",ans,max(ans,ans1));
}
P2194
P2812 校园网络【[USACO]Network of Schools加强版】
//邻接表
#include <bits/stdc++.h>
using namespace std;
;
;
int n,num,sum,cnt,ans1,ans2;
int low[N],dfn[N],head[N],size[N],bel[N];
bool vis[N],mark[N],mark1[N];
struct node {
int v,nx;
}e[M];
template<class T>inline void read(T &x) {
x = ;;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
stack<int>s;
void tarjan(int u) {
dfn[u] = low[u] = ++ cnt;;
vis[u] = ;
s.push(u);
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[v]) low[u] = min(low[u],dfn[v]);
}
if(dfn[u] == low[u]) {
;sum ++;
while(x != u) {
x = s.top(),s.pop();
bel[x] = sum,vis[x] = ;
size[sum] ++;
}
}
}
int main(int argc, char const *argv[]) {
memset(head,-,sizeof(head));
read(n);
,x; i <= n; ++ i) {
; j <= n + ; ++ j) {
read(x);
) break;
add(i,x);
}
}
; i <= n; ++ i) if(!dfn[i]) tarjan(i);
; i <= n; ++ i) {
for(int j = head[i]; ~j; j = e[j].nx) {
if(bel[i] != bel[e[j].v]) {
mark[bel[e[i].v]] = ;
mark1[bel[i]] = ;
}
}
}
; i <= sum; ++ i) {
if(!mark[i]) ans1 ++;
if(!mark1[i]) ans2 ++;
}
printf("%d\n%d\n", ans1,ans2);
;
}
P2812
/*
主体还是一个tarjan
因为最后还会组成n对情侣的话
找恋人的人和恋人和男方会在一个联通块内
因为男女必须成对出现，所以联通块内的点得个数为偶数，所以联通块内每个人都会配对
经过路径是boy1->girl2->boy2->gril1->boy1
*/
#include <bits/stdc++.h>
using namespace std;
;
;
int n,m,k,num,sum,cnt,tmp;
int head[N],dfn[N],bel[N],low[N],sta[N];
bool vis[N];
string g,b;
map<string,int>mp;
struct node {
int v,nx;
}e[M];
template<class T>inline void read(T &x) {
x = ;;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
stack<int>s;
void tarjan(int u) {
dfn[u] = low[u] = ++cnt;
vis[u] = ;
s.push(u);
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[v]) low[u] = min(low[u],dfn[v]);
}
if(dfn[u] == low[u]) {
int x;sum ++;
while(u != x) {
x = s.top(),s.pop();
vis[x] = ,bel[x] = sum;
}
}
}
int main() {
memset(head,-,sizeof(head));
read(n);
; i <= n; ++ i) {
cin>>g>>b;
mp[g] = i,mp[b] = i + n;
add(i,i + n);
}
read(m);
; i <= m; ++ i) {
cin>>g>>b;
add(mp[g],mp[b]),add(mp[b],mp[g]);
}
; i <= n * ; ++ i) if(!dfn[i]) tarjan(i);
; i <= n; ++ i) {
if(bel[i] == bel[i + n]) printf("Unsafe\n");
else printf("Safe\n");
}
;
}
P1407
以下两个可能用到其他小知识
//tarjan+最短路
#include <bits/stdc++.h>
using namespace std;
;
;
const int INF = 0x3f3f3f3f;
int n,m,sum,num,num_new,cnt;
int dfn[N],low[N],head[N],head_new[N],bel[N],dis[N];
bool vis[N],vis_new[N];
struct edge {
int v,nx,w;
}e[N];
struct edge_new {
int v,nx,w;
}e_new[N];
struct node {
int id,dis;
bool operator < (const node &l) const {
return dis > l.dis;
}
};
template<class T>inline void read(T &x) {
x = ;;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return;
}
inline void add(int u,int v,int w) {
e[++num].nx = head[u],e[num].v = v,e[num].w = w,head[u] = num;
}
inline void add_new(int u,int v,int w) {
e_new[++num_new].nx = head_new[u],e_new[num_new].v = v,e_new[num_new].w = w,head_new[u] = num_new;
}
stack<int>s;
void tarjan(int u) {
dfn[u] = low[u] = ++ cnt;
vis[u] = ;
s.push(u);
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) tarjan(v),low[u] = min(low[u],low[v]);
else if(vis[v]) low[u] = min(low[u],dfn[v]);
}
if(low[u] == dfn[u]) {
int x;sum ++;
while(u != x) {
x = s.top(),s.pop();
vis[x] = ,bel[x] = sum;
}
}
}
void dijkstra(int s) {
priority_queue<node>q;
memset(dis,INF,sizeof(dis));
memset(vis_new,,sizeof(vis_new));
dis[s] = ;
q.push((node){s,});
while(!q.empty()) {
node d = q.top();q.pop();
int u = d.id;
if(vis_new[u]) continue;
vis_new[u] = ;
for(int i = head_new[u]; ~i; i = e_new[i].nx) {
int v = e_new[i].v;
if(dis[v] > dis[u] + e_new[i].w) {
dis[v] = dis[u] + e_new[i].w;
q.push((node){v,dis[v]});
}
}
}
}
int main() {
memset(head,-,sizeof(head));
memset(head_new,-,sizeof(head_new));
read(n),read(m);
,x,y,z; i <= m; ++ i) read(x),read(y),read(z),add(x,y,z);
; i <= n; ++ i) if(!dfn[i]) tarjan(i);
; i <= n; ++ i)
for(int j = head[i]; ~j; j = e[j].nx) {
int v = e[j].v;
if(bel[i] != bel[v]) add_new(bel[i],bel[v],e[j].w);
}
dijkstra(bel[]);
printf("%d\n",dis[bel[n]]);
;
}
/*
tarjan缩点求最小路径覆盖集
*/
#include <bits/stdc++.h>
using namespace std;
;
;
int t, n, m, num, num_new, sum, cnt, ans;
int head[N], low[N], dfn[N], link[N], head_new[N], bel[N];
bool vis[N], vis_new[N];
struct node {
int v, nx;
} e[M], e_new[M];
template<class T>inline void read(T &x) {
x = ; ; char ch = getchar();
while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
+ ch - ', ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u, int v) {
e[++num].nx = head[u], e[num].v = v, head[u] = num;
}
inline void add_new(int u, int v) {
e_new[++num_new].nx = head_new[u], e_new[num_new].v = v, head_new[u] = num_new;
}
stack<int>s;
void tarjan(int u) {
dfn[u] = low[u] = ++cnt;
vis[u] = ;
s.push(u);
for (int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if (!dfn[v]) tarjan(v), low[u] = min(low[u], low[v]);
else if (vis[v]) low[u] = min(low[u], dfn[v]);
}
if (low[u] == dfn[u]) {
int x; sum++;
while (x != u) {
x = s.top(), s.pop();
bel[x] = sum, vis[x] = ;
}
}
}
bool dfs(int u) {
for (int i = head_new[u]; ~i; i = e_new[i].nx) {
int v = e_new[i].v;
if (!vis_new[v]) {
vis_new[v] = ;
|| dfs(link[v])) {
link[v] = u;
;
}
}
}
;
}
int main(int argc, char const *argv[]) {
read(t);
while (t --) {
read(n), read(m);
memset(vis, , sizeof(vis));
memset(low, , sizeof(low));
memset(dfn, , sizeof(dfn));
memset(bel, , sizeof(bel));
memset(head, -, sizeof(head));
memset(link, -, sizeof(link));
memset(head_new, -, sizeof(head_new));
memset(e, , sizeof(e));
memset(e_new, , sizeof(e_new));
ans = num = cnt = num_new = sum = ;
, x, y; i <= m; ++ i) read(x), read(y), add(x, y);
; i <= n; ++i) if (!dfn[i]) tarjan(i);
; i <= n; ++i)
for (int j = head[i]; ~j; j = e[j].nx) {
int v = e[j].v;
if (bel[i] != bel[v]) add_new(bel[i], bel[v]);
}
; i <= sum; ++i) {
memset(vis_new, , sizeof(vis_new));
if (dfs(i)) ans ++;
}
printf("%d\n", sum - ans);
}
;
}
HDU 3861
Tarjan割点&&割边
割点
割点：在无向连通图中，删除一个顶点v及其相连的边后，原图从一个连通分量变成了两个或多个连通分量，则称顶点v为割点，同时也称关节点(Articulation Point)。
一个没有关节点的连通图称为重连通图(biconnected graph)。若在连通图上至少删去k 个顶点才能破坏图的连通性，则称此图的连通度为k。
some小例子
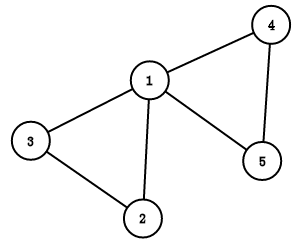
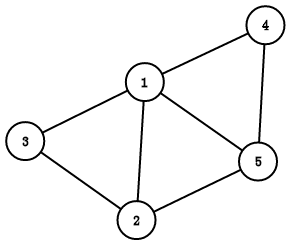
割点为1的图（删去1和他的边图变成两部分） 连通度为2的图
首先明白几个概念
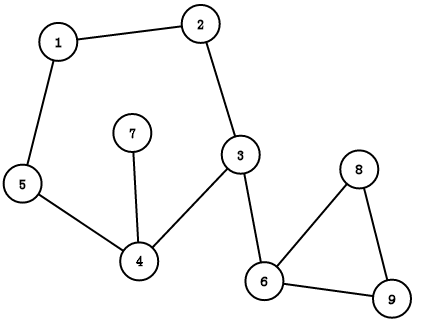
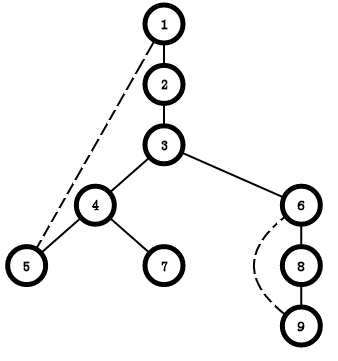
（a） （b）
概念：
DFS树：用DFS对图进行遍历时，按照遍历次序的不同，我们可以得到一棵DFS搜索树，如图(b)所示。
树边：如（b）中的实线所示，可理解为在DFS过程中访问未访问节点时所经过的边
回边：如（b）中的虚线所示，可理解为在DFS过程中遇到已访问节点时所经过的边。
观察我们的DFS树（b），发现它有两种情况可能是割点：
1、对于一个根节点u，若有两个及以上的子树，说明u是割点
2、对于非叶子节点u（非根节点），若其子树均没有连向u祖先节点的回边，说明删掉u后，根节点与子树不再相连，则u是割点
对根节点很好处理，只要记录一下它的子树个数就好了，对于非叶节点呢
对！用low数组
我们用low记录节点u或u的子树通过非父子边追溯到最早的祖先节点
low[u] = min(low[u],low[v])（当(u,v)是树边）
low[u] = min(low[u],dfn[v])（当(u,v)是回边且v不等于u的父节点）
对于情况2，(u,v)是树边且当 low[v] ≥ dfn[u] 时，节点u是割点，因为v能回溯到的最早祖先不是u就是v，所以v并不能连到u的祖先上，当删去u时，v和u的祖先不相连，即u是割点
fa的意思就是从哪个点搜过来的，因为是无向图，可能还会搜到之前的点
代码实现：
//cut标记当前点是否是割点
void tarjan(int u,int fa) {
dfn[u] = low[u] = ++cnt;
;//记录子树个数
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) {
tarjan(v,u);
low[u] = min(low[u],low[v]);
;//情况2
if(u == fa) child ++;
}
low[u] = min(low[u],dfn[v]);
}
&& u == fa) cut[u] = ;//情况1
}
例题：
#include <bits/stdc++.h>
using namespace std;
;
int n,m,num,cnt,tot;
int dfn[N],low[N],head[N];
bool cut[N];
struct node {
int v,nx;
}e[N];
template<class T>inline void read(T &x) {
x = ;;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
void tarjan(int u,int fa) {
dfn[u] = low[u] = ++cnt;
;
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) {
tarjan(v,u);
low[u] = min(low[u],low[v]);
;
if(u == fa) child ++;
}
low[u] = min(low[u],dfn[v]);
}
&& u == fa) cut[u] = ;
}
int main() {
memset(head,-,sizeof(head));
read(n),read(m);
,x,y; i <= m; ++ i) read(x),read(y),add(x,y),add(y,x);
; i <= n; ++ i) if(!dfn[i]) tarjan(i,i);
; i <= n; ++ i) if(cut[i]) tot ++;
printf("%d\n",tot);
; i <= n; ++ i) if(cut[i]) printf("%d ",i);
;
}
P3388
//输出最小的割点编号
#include <bits/stdc++.h>
using namespace std;
;
int n,m,k,num,cnt,x,y;
int dfn[N],low[N],head[N];
bool cut[N],vis[N];
struct node {
int nx,v;
}e[N];
template<class T>inline void read(T &x) {
x = ;;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
void tarjan(int u,int fa) {
dfn[u] = low[u] = ++cnt;
;
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) {
tarjan(v,u);
low[u] = min(low[u],low[v]);
;
if(u == fa) child ++;
}
low[u] = min(low[u],dfn[v]);
}
) cut[u] = ;
}
void dfs(int u) {
vis[u] = ;
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!vis[v]) dfs(v);
}
}
int main() {
memset(head,-,sizeof(head));
read(n);
while(scanf("%d%d",&x,&y)) {
&& y == ) break;
add(x,y),add(y,x);
}
; i <= n; ++ i) if(!dfn[i]) tarjan(i,i);
read(x),read(y);
; i <= n; ++ i) {
if(cut[i]) {
memset(vis,,sizeof(vis));
vis[i] = ;
dfs(x);
if(!vis[y]) {
cout<<i;
;
}
}
}
cout<<"No solution";
;
}
P5058
割边
割边的话其实也差不多甚至更简单
割边：也叫桥，当且仅当去掉该边之后的子图不连通
割边是用在无向图内的
割边不用记录子树情况，然后再改一句话把low[v] >= dfn[u]改为low[v] > dfn[u]
因为我们割点的时候是把当前节点u的所有的边都删去，而割边只能删一条边，显然，如果u，v之间有两条边的话，如果其中删掉一条边，另一条还和u相连，原图还保持连通
代码：
#include <bits/stdc++.h>
using namespace std;
;
int n,m,num,cnt;
int low[N],dfn[N],head[N];
struct node {
int v,nx,id;
}e[N];
template<class T>inline void read(T &x) {
x = ;;char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'),ch = getchar();
+ ch - ',ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u,int v) {
e[++num].nx = head[u],e[num].v = v,head[u] = num;
}
void tarjan(int u,int fa) {
dfn[u] = low[u] = ++cnt;
for(int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if(!dfn[v]) {
tarjan(v,u);
low[u] = min(low[u],low[v]);
if(low[v] > dfn[u]) printf("%d -- %d is a Cutting edge\n",u,v);
}
else if(v != fa) low[u] = min(low[u],dfn[v]);
}
}
int main(int argc, char const *argv[]) {
memset(head,-,sizeof(head));
read(n),read(m);
,x,y; i <= m; ++ i) {
read(x),read(y);
add(x,y),add(y,x);
}
; i <= n; ++ i) if(!dfn[i]) tarjan(i,i);
;
}
点双连通分量&&边双连通分量
这东西我是现学现卖的，可能会有些地方不详细
既然我们要求点双连通分量和边双连通分量，那我们就要知道它们是什么
连通：在无向图中，所有的点能相互到达
连通分量：相互连通的子图
点双连通分量：简单说，就是没有割点的子图，也就是删掉一个点后，图仍连通性
边双连通分量：简单说，就是没有割边的子图，也就是删掉一个边后，图仍连通性
如果先看具体定义，出门右转自己搜吧（其实是我懒得放百度链接，万一你们都用wiki呢）
这样说很抽象的话，还是来两张图好了
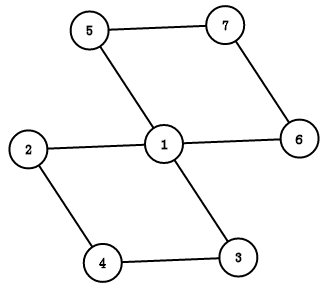
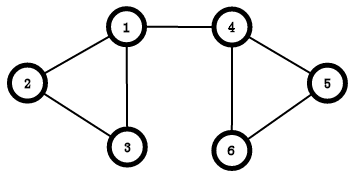
（1） （2）
如图（1）所示：1是割点，{1,2,4,3} 是一个点双连通分量，{1,5,7,6} 也是一个点双连通分量，不难发现，割点可能存在于多个点双连通分量里，而其他点只可能存在于一个点双连通分量里，同时，{1,2,3,4,5,6,7,8} 也是一个边双连通 分量；
如图（2）所示，1-4 是割边，在这个图内 {1,2,3} 和 {4,5,6} 分别组成了连个边双连通分量
求点双连通分量：
对于点双连通分量，在求割点的时候就可以顺便求出，但这是我们要建立一个栈，然后在搜索图的时候，让边入栈，如果遇到 low[v] ≥ dfn[u] 即u是割点的时候，将 u - v 这条边之上的边全部弹出，这些边以及相邻的点就组成了一个点双连通分量，割点可能会属于多个双连通分量，其余的点只会属于一个双连通分量；
文字还是太无力，简单走一下流程：
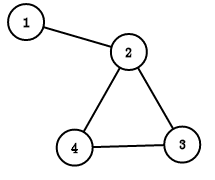
一张简单图：
我们从1开始搜索，dfn[1] = 1,low[1] = 1
搜到2，2没被搜过（时间戳dfn），dfn[2] = 2,low[2] = 2，边 1-2 入栈，栈内元素：{1-2}
搜到3，3没被搜过，dfn[3] = 3,low[3] = 3，边2-3入栈，栈内元素：{1-2，2-3}
搜到4，4没被搜过，dfn[4] = 4,low[4] = 4，边3-4入栈，栈内元素：{1-2，2-3，3-4}
搜4，搜到了2，2被搜过，且4不是2搜过来的，low[4] = min(low[4],dnf[2]) = 2，2-4入栈，栈内元素：{1-2，2-3，3-4，4-2}
回到3，low[3] = min(low[3],low[4]) = 2
回到2，low[3] == low[2] 所以 2 是割点，弹栈，将边 2-3 以上的边全部弹出，将他们边连的顶点存入一个数组内，记为一个双连通分量
最后回到1，dfn[1] == low[1]，弹栈，所以{1,2}也是一个点双连通分量
这样，我们就找到了点双联通分量 {1,2}，{2,3,4}；
这里同样还是用fa记录从那个点搜到了当前点
code：
int dfn[N], low[N], head[N], bel_bcc[N], mn[N];
bool cut[N];
struct edge {//从u到v的边
int u, v;
};
struct node {//建图用
int v, nx;
} e[N];
stack<edge>s;//栈内存的是边，
vector<int>bcc[N];
inline void add(int u, int v) {
e[++num].nx = head[u], e[num].v = v, head[u] = num;
}
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++cnt;
;
for (int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if (!dfn[v]) {
s.push((edge) {u, v});
child ++;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {//是割点
cut[u] = ;
bcc_sum ++;//点双的个数++
// bcc[bcc_sum].clear();
) {
edge d = s.top(); s.pop();
if (bel_bcc[d.u] != bcc_sum) bcc[bcc_sum].push_back(d.u),bel_bcc[d.u] = bcc_sum;//标记某点在这个电双块内
if (bel_bcc[d.v] != bcc_sum) bcc[bcc_sum].push_back(d.v),bel_bcc[d.v] = bcc_sum;
if (d.u == u && d.v == v) break;//弹栈一直到u-v
}
}
} else if (dfn[v] < dfn[u] && v != fa) {//回边
s.push((edge) {u, v});
low[u] = min(low[u], dfn[v]);
}
}
&& child == ) cut[u] = ;//把根节点看做普通节点了，所以下面最后的特殊判断必需。
}
求边双连通分量：
边双联通分量可能简单些，
简单说，就是找到桥（割边）后，把桥删掉，剩下很多连通块，每一个连通块就是一个边双连通分量
因为把图中的桥删掉后，剩下的边都不是桥，既然不是桥，就不能把连通块分成多部分，所以剩下的连通块满足边双连通的定义，所以剩余的连通块都是边双联通
桥不属于任何一个边双连通分量，其余的边和每个顶点，都属于且只属于一个边连通分量
所以我们要做的就只有求桥，删边，染色DFS
code：
;
];
void tarjan(int x, int in_edge) {
dfn[x] = low[x] = ++cnt;
for (int i = head[x]; ~i; i = e[i].nx) {
int y = e[i].y;
if (!dfn[y]) {
tarjan(y, i);
low[x] = min(low[x], low[y]);
] = ;
}
))
low[x] = min(low[x], dfn[y]);
}
}
;
void dfs(int x, int color) {
block[x] = color;
; i = e[i].nx) {
int y = e[i].y;
if (cut[i]) continue;
if (!block[y]) dfs(y, color);
}
}
void get_edccs() {
; i <= n; i++)
if (!block[i])
dfs(i, ++dcc);
}
例题：
Tarjan应用之——LCA
既然说到了Tarjan，那就不得不说一下它的应用，求LCA
Tarjan求LCA是一个O(n+m)的离线做法，查询是O(1)的
Tarjan求LCA其实就是深搜+并查集
先把算法流程摆上
1、任意选一个点为根节点
2、把当前节点u的father设为u，看与u相邻的点v，若v没被搜过，深搜v，深搜完后，把father[v]设成u
3、搜完一个点u后，开始判断与它相关的询问，如果另一个点被搜过，LCA就是另一个点的祖先
我相信看完了我的描述之后，你们还是不知道什么意思
那我们还是手模一下它的流程：
假设我们有这么一张图：
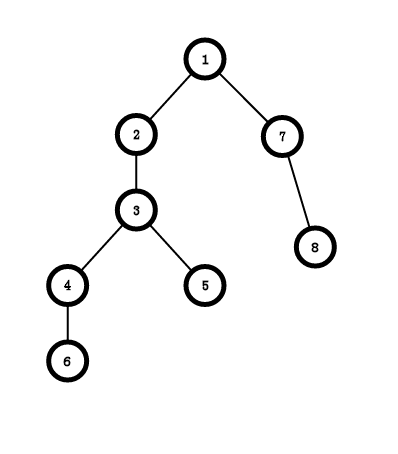
我们要查询2-4，5-6，4-7，6-8的LCA
从1开始搜索，fa[1] = 1,vis[1] = 1
搜到2，fa[2] = 2,vis[2] = 1
搜到3，fa[3] = 3,vis[3] = 1;
搜到4，fa[4] = 4,vis[4] = 1;
搜到6，fa[6] = 6,vis[6] = 1;
到此为止，我们就得到了这样的图
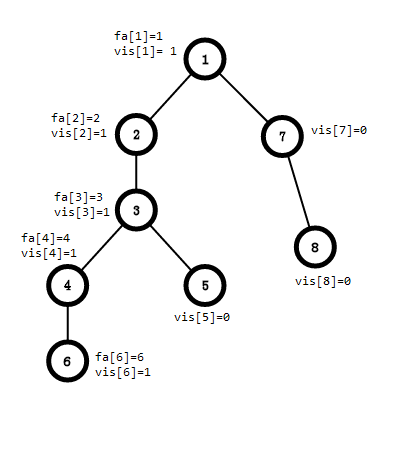
发现6没有别的连边了，开始回溯
我们看到有一个关于6的询问6-8，发现vis[8] = 0,不管
回溯到4，fa[6]=4，发现和4有关的询问2-4，于是lca(2,4) = find(2) = 2 ，记录一下//find是找祖宗函数，并查集里常用
回溯到3，发现还有一条边，继续搜
搜到5，fa[5] = 5,vis[5] = 1
5没有别的连边，找和5相关的询问5-6，lca(5,6) = find(6) = 3，记录一下
回溯到3，fa[5] = 3
回溯到2，fa[3] = 2
回溯到1，fa[2] = 1
这样左边的就搜完了
得到
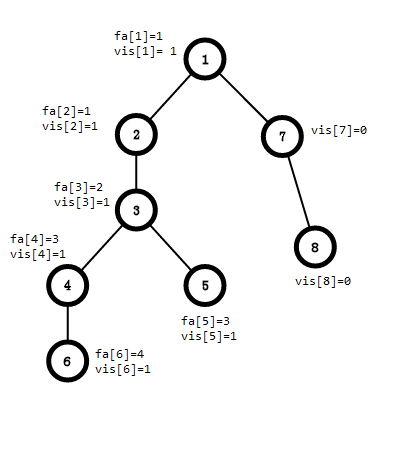
回溯到1
继续搜，搜到7，fa[7] = 7,vis[7] = 1
搜到8，fa[8] = 8,vis[8] = 1;
8没有其他的连边，发现有一个和8相关的询问6-8，lca(6,8) = find(6) = 1
回溯到7，fa[8] = 7,发现一个和7相关的询问4-7，lca(4,7) = find(4) = 1
回溯到1，fa[7] = 1
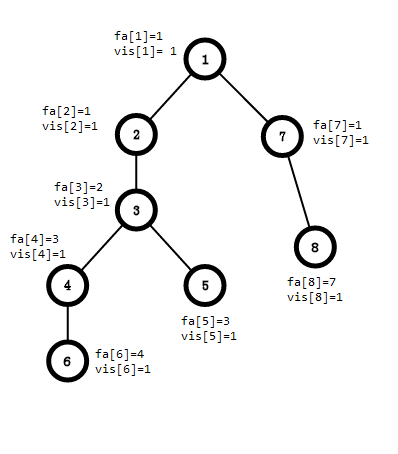
到此为止，我们已经把整棵树dfs了一遍，也处理处了所有的询问的结果
最后直接输出就好了
看代码：
//e是记录原图，_e是记录询问
//lca记录的是第i组询问的结果
#include <bits/stdc++.h>
using namespace std;
;
int n, m, k, num, _num;
int fa[N], head[N], _head[N];
bool vis[N];
struct node {
int v, nx, lca;
} e[N], _e[N];
template<class T>inline void read(T &x) {
x = ; ; char ch = getchar();
while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
+ ch - ', ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u, int v) {
e[++num].nx = head[u], e[num].v = v, head[u] = num;
}
inline void _add(int u, int v) {
_e[++_num].nx = _head[u], _e[_num].v = v, _head[u] = _num;
}
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void tarjan(int u) {
fa[u] = u, vis[u] = ;
for (int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if (!vis[v]) {
tarjan(v);
fa[v] = u;
}
}
for (int i = _head[u]; ~i; i = _e[i].nx) {
int v = _e[i].v;
if (vis[v]) {
_e[i].lca = find(v);
) _e[i + ].lca = _e[i].lca;//因为是加的双向边，奇数边是从父到子加的，偶数边是从子到父加的，两者相同
].lca = _e[i].lca;
}
}
}
int main(int argc, char const *argv[]) {
memset(head, -, sizeof(head));
memset(_head, -, sizeof(_head));
read(n), read(m), read(k);
, x, y; i < n; ++ i) read(x), read(y), add(x, y), add(y, x);
, x, y; i <= m; ++ i) read(x), read(y), _add(x, y), _add(y, x);
tarjan(k);
; i <= m; ++ i) printf(].lca);
;
}
例题：
P2912 [USACO08OCT]牧场散步Pasture Walking
//dis[i]表示到i的距离
//这一类题，dis直接在Tarjan中计算就好了
#include <bits/stdc++.h>
using namespace std;
;
int n, m, num, _num;
int head[N], _head[N], fa[N], dis[N];
bool vis[N];
struct node {
int v, nx, w, lca, ans;
} e[N], _e[N];
template<class T>inline void read(T &x) {
x = ; ; char ch = getchar();
while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
+ ch - ', ch = getchar();
x = f ? -x : x;
return ;
}
inline void add(int u, int v, int w) {
e[++num].nx = head[u], e[num].v = v, e[num].w = w, head[u] = num;
}
inline void _add(int u, int v) {
_e[++_num].nx = _head[u], _e[_num].v = v, _head[u] = _num;
}
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void tarjan(int u) {
fa[u] = u, vis[u] = ;
for (int i = head[u]; ~i; i = e[i].nx) {
int v = e[i].v;
if (!vis[v]) {
dis[v] = dis[u] + e[i].w;
tarjan(v);
fa[v] = u;
}
}
for (int i = _head[u]; ~i; i = _e[i].nx) {
int v = _e[i].v;
if (vis[v]) {
_e[i].lca = find(v);
_e[i].ans = dis[u] + dis[v] - dis[_e[i].lca] * ;
) _e[i + ].lca = _e[i].lca, _e[i + ].ans = _e[i].ans;
].lca = _e[i].lca, _e[i - ].ans = _e[i].ans;
}
}
}
int main(int argc, char const *argv[]) {
memset(head, -, sizeof(head));
memset(_head, -, sizeof(_head));
read(n), read(m);
, x, y, z; i < n; ++ i) read(x), read(y), read(z), add(x, y, z), add(y, x, z);
, x, y; i <= m; ++ i) read(x), read(y), _add(x, y), _add(y, x);
tarjan();
; i <= m; ++ i) printf(].ans);
;
}
P2912
一般的LCA都可以做的吧。。（我做题少，而且都是用倍增做的，如有什么不可以题的话还请告知我一下）
Tarjan总结（缩点+割点(边)+双联通+LCA+相关模板）的更多相关文章
- Tarjan算法应用 （割点/桥/缩点/强连通分量/双连通分量/LCA(最近公共祖先)问题）（转载）
Tarjan算法应用 (割点/桥/缩点/强连通分量/双连通分量/LCA(最近公共祖先)问题)(转载) 转载自:http://hi.baidu.com/lydrainbowcat/blog/item/2 ...
- Tarjan的缩点&&割点概述
What is Tarjan? Tarjan,是一种用来解决图的联通性的一种有效途径,它的一般俗称叫做:缩点.我们首先来设想一下: 如果我们有一个图,其中A,B,C构成一个环,那么我们在某种条件下,如 ...
- hdu 2460 poj 3694 (双联通+LCA)
在给出的两个点上加一条边,求剩下桥的数量,,不会LCA在线,就用了最普通的,先Tarjan双联通缩点,然后将缩完的图建成一棵树,树的所有边就是桥了,如果在任意两点间加一条边的话,那么从两点到最近公共祖 ...
- Tarjan应用:求割点/桥/缩点/强连通分量/双连通分量/LCA(最近公共祖先)【转】【修改】
一.基本概念: 1.割点:若删掉某点后,原连通图分裂为多个子图,则称该点为割点. 2.割点集合:在一个无向连通图中,如果有一个顶点集合,删除这个顶点集合,以及这个集合中所有顶点相关联的边以后,原图变成 ...
- (转)Tarjan应用:求割点/桥/缩点/强连通分量/双连通分量/LCA(最近公共祖先)
基本概念: 1.割点:若删掉某点后,原连通图分裂为多个子图,则称该点为割点. 2.割点集合:在一个无向连通图中,如果有一个顶点集合,删除这个顶点集合,以及这个集合中所有顶点相关联的边以后,原图变成多个 ...
- 无向连通图求割点（tarjan算法去掉改割点剩下的联通分量数目）
poj2117 Electricity Time Limit: 5000MS Memory Limit: 65536K Total Submissions: 3603 Accepted: 12 ...
- POJ 3694 Network 无向图双联通+LCA
一开始题目没看清楚,以为是增加那条边后还有多少桥,所以就当做是无向图tarjan缩点后建树,然后求u,v的最近公共祖先,一直wa. 后来再看题目后才发现边放上去后不会拿下来了,即增加i条边后桥的数量. ...
- HDU4612 Warm up —— 边双联通分量 + 重边 + 缩点 + 树上最长路
题目链接:http://acm.split.hdu.edu.cn/showproblem.php?pid=4612 Warm up Time Limit: 10000/5000 MS (Java/Ot ...
- POJ3177 Redundant Paths —— 边双联通分量 + 缩点
题目链接:http://poj.org/problem?id=3177 Redundant Paths Time Limit: 1000MS Memory Limit: 65536K Total ...
随机推荐
- Python_每日习题_0006_斐波那契数列
程序设计: 斐波那契数列(Fibonacci sequence),从1,1开始,后面的每一项等于前面两项之和. 图方便就递归实现,图性能就用循环. # for 循环 target = int(inpu ...
- PHP实用代码片段（二）
1. 转换 URL:从字符串变成超链接 如果你正在开发论坛,博客或者是一个常规的表单提交,很多时候都要用户访问一个网站.使用这个函数,URL 字符串就可以自动的转换为超链接. function mak ...
- 获取环境变量,0x000000cb 操作系统找不到已输入的环境选项
include "stdafx.h" #include <Windows.h> #include <iostream> #pragma warning(di ...
- flex实现三栏等分布局
前言 在实际开发中,我们经常会想要实现的一种布局方式就是三栏等分布局,那么我们如何来解决这个问题呢? 解决 方法一:flex 外层容器也就是ul设置display:flex,对项目也就是li设置fle ...
- java学习之—递归实现二分查找法
/** * 递归实现二分查找法 * Create by Administrator * 2018/6/21 0021 * 上午 11:25 **/ class OrdArray{ private lo ...
- java.util.concurrent.TimeoutException: Idle timeout expired: 300000/300000 ms
Request idle timed out at 123000 ms. That means there was no activity (read or write) for 123000 ms ...
- 老男孩python学习自修【第三天】列表用法
列表的使用: list.append(value) 向列表增加元素 list.insert(index, value) 向列表指定元素插入元素 list.extend(newlist) 用新的列表扩展 ...
- 怎样利用ADO中的adoquery进行缓存更新？？？？？(100分)
我用BDE时,用query与updatesql相结合进行缓存更新,但是在ADO中没有updatesql,只有用adoquery,在DBGRID中,用CANCELUPADTE,只能取消一条记录,烦恼不已 ...
- 一、VScode构建.NET应用程序
一.准备工具 1.安装.NET SDK(软件开发工具包) https://microsoft.com/net/core 2.安装VScode并安装 3.安装VS Code C# extension(即 ...
- XCTF 4th-WHCTF-2017 creakme
exe文件 运行一下 随便输一下 ps.这个曹操身边的故事挺有意思的 但是没啥卵用....... 查一下壳无壳 ida载入 发现找不到main函数 直接看start感觉逻辑乱乱的(萌新求不喷..... ...