剑指offer(10)

题目：

　　输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

思路：

　　如果忽略题目中“并保证奇数和奇数，偶数和偶数之间的相对位置不变，有以下解法，设两个指针，前面一个指针停在偶数位置，后面一个指针停在奇数位置，然后交换，直达第一个指针跑到第二个指针之后结束，

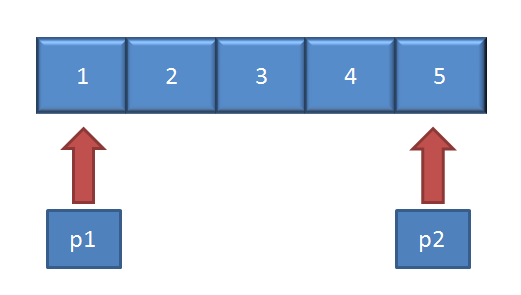
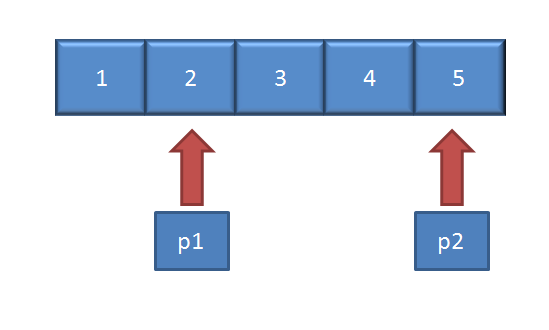
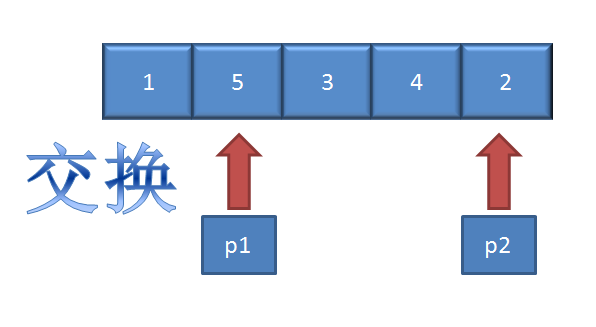
public class Solution {
    public void reOrderArray(int [] array) {
        int point1 = 0;
        int point2 = array.length-1;

        while(point1<point2){
            //这里要注意一下运算符的优先级
            while(point1<point2 && (array[point1]&0x1)!=0){
                point1++;
            }
            while(point1<point2&&(array[point2]&0x1)==0){
                point2--;
            }
            if(point1<point2){
                int temp = array[point1];
                array[point1] = array[point2];
                array[point2] = temp;
            }
        }
    }
}    

这里为了增强代码的重用性，可以将判断标准另起一个函数.

回到原题，我们这里可以设置两个栈，分别从头到尾读数，把奇偶数分开到两个栈里，然后按要求从数组后面开始弹栈。

import java.util.Stack;
public class Solution {
    public void reOrderArray(int [] array) {

        Stack stack1 = new Stack();
        Stack stack2 = new Stack();

        int oddLength = 0;
        int evenLength = 0;

        for(int i=0;i<array.length;i++){
            if((array[i]&0x1)==1){
                stack1.push(array[i]);
                oddLength++;
            }else{
                stack2.push(array[i]);
                evenLength++;
            }
        }

        for(int i=array.length-1;i>=array.length-evenLength;i--){
            array[i] = (int)stack2.pop();
        }
        for(int i=oddLength-1;i>=0;i--){
            array[i] = (int)stack1.pop();
        }
    }
}