二叉查找树（BST)、平衡二叉树(AVL树)（只有插入说明）

二叉查找树（BST)、平衡二叉树(AVL树)（只有插入说明）

二叉查找树(BST)

　　特殊的二叉树，又称为排序二叉树、二叉搜索树、二叉排序树。

　　二叉查找树实际上是数据域有序的二叉树，即对树上的每个结点，都满足其左子树上所有结点的数据域均小于或等于根结点的数据域，右子树上所有结点的数据域均大于根结点的数据域。如下图所示：

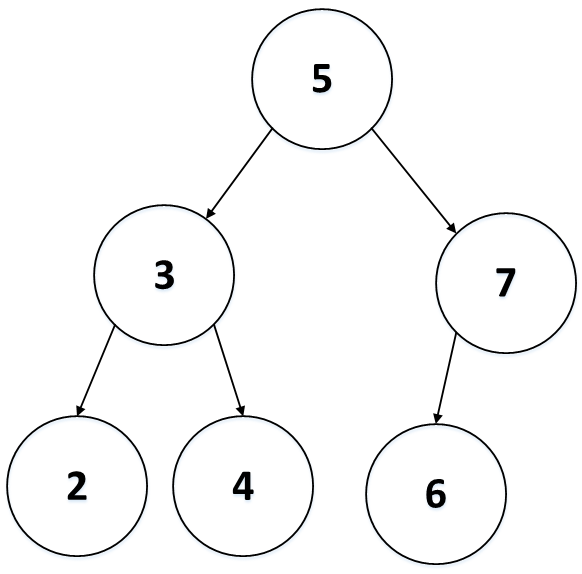
二叉查找树通常包含查找、插入、建树和删除操作。

二叉查找树的创建

对于一棵二叉查找树，其创建与二叉树的创建很类似，略有不同的是，二叉查找树，为了保证整棵树都关于根结点的大小呈左小右大的特征，在创建时，需要根据当前结点的大小来判断插入位置，给出如下代码：

template<typename T>
void  BSTree<T>::createBSTreeByFile(ifstream &f){
    T e;
    queue<BSNode<T>*> q;

    while(!f.eof()){
        InputFromFile(f, e);
        Insert(root, e);
    }
}

template<typename T>
void BSTree<T>::Insert(BSNode<T>* &t, T x){//得用指针的引用，不然传参时由于形参实例化，并不能成功创建二叉树

    if(t==NULL){
        t = new BSNode<T>;
        t->data = x;
        t->lchild = t->rchild = NULL;
        return;
    }

    if(x<=t->data){
        Insert(t->lchild, x);
    }
    else{
        Insert(t->rchild, x);
    }
}

二叉查找树的查找

二叉查找树的查找有递归和非递归两种，对于递归方式，其递归边界为树的终止结点，非递归方式则采取对树中所有结点采取BFS或者DFS进行遍历的方式。

对于非递归方式，给出采取DFS的遍历方式，在这种方式中，通常采用入栈的方式，来访问每个结点，而根据访问的先后顺序，又分为，前序、中序和后序三种遍历方式。以前序遍历为例，通常以根、左、右的顺序访问遍历每个结点，而中序遍历方式，则以左、根、右的顺序遍历，后序则以左右根的顺序来访问。下面给出三种遍历方式的代码：前序遍历：

 1 template<typename T>
 2 void BSTree<T>::PreOrderTraverse(void(*visit)(BSNode<T>&))const{
 3     stack<BSNode<T>*> s;
 4     BSNode<T> *t = root;
 5     while(NULL!=t || !s.empty()){
 6         if(NULL!=t){
 7             s.push(t);
 8             visit(*t);
 9             t = t->lchild;
10         }
11         else{
12             t = s.top();
13             s.pop();
14             t = t->rchild;
15         }
16     }
17     cout<<endl;
18 }

中序遍历：

 1 template<typename T>
 2 void BSTree<T>::InOrderTraverse(void(*visit)(BSNode<T>&))const{
 3     stack<BSNode<T>*> s;
 4     BSNode<T> *q;
 5
 6     q = root;
 7
 8     while(!s.empty()||q!=NULL){
 9         if(q!=NULL){
10             s.push(q);
11             q = q->lchild;
12         }
13         else{
14             q = s.top();
15             s.pop();
16             visit(*q);
17             q = q->rchild;
18         }
19     }
20     cout<<endl;
21 }

后序遍历，对于后序遍历，直接采用入栈的方式进行访问，是不行的，因为根结点被访问两次，无法保证你在弹栈后，对该结点如何操作，因此，需要另设置一个flag参数，来指明该节点是否左右子树都访问过，代码如下，我这里是令定义一个结构体，来实现：

/*结构体部分*/
enum Tags{Left, Right};

template<typename T>struct StackElem
{
    BSNode<T> *p;
    Tags flag;
};

/*后序遍历代码部分*/
template<typename T>
void BSTree<T>::PostOrderTraverse(void(*visit)(BSNode<T>&))const{
    StackElem<T> se;
    stack<StackElem<T> > s;

    BSNode<T> *t;
    t = root;

    if(t==NULL){
        return;
    }
    while(t!=NULL||!s.empty()){
        while(t!=NULL){
            se.flag = Left;
            se.p = t;
            s.push(se);
            t = t->lchild;
        }
        se = s.top();
        s.pop();
        t = se.p;
        if(se.flag==Left){
            se.flag = Right;
            s.push(se);
            t = t->rchild;
        }
        else{
            visit(*t);
            t = NULL;
        }
    }
}

以下是递归实现部分，递归实现，则是以二叉树边界为递归边界，前面已经说过了，其余逻辑与非递归一致，因为递归的过程，可以看作是一个入栈和弹栈的过程，即，在未到达边界时，通过递归，来访问下一个结点，例如左结点，当触及边界，则访问该结点，由于每次递归状态都被计算机保存，因此，在访问一个结点以后，返回上一个结点的状态，会依次访问上去。

递归前序遍历：

 1 template<typename T>
 2 void BSTree<T>::PreTraverse(BSNode<T> *t, void(*visit)(BSNode<T>&))const{
 3     if(t==NULL){
 4         return;
 5     }
 6     else{
 7         visit(*t);
 8         PreTraverse(t->lchild, visit);
 9         PreTraverse(t->rchild, visit);
10     }
11 }

递归中序遍历：

 1 template<typename T>
 2 void BSTree<T>::InTraverse(BSNode<T> *t, void(*visit)(BSNode<T>&))const{
 3     if(t==NULL){
 4         return;
 5     }
 6     else{
 7         InTraverse(t->lchild, visit);
 8         visit(*t);
 9         InTraverse(t->rchild, visit);
10     }
11 }

递归后序遍历：

1 template<typename T>
2 void BSTree<T>::PostTraverse(BSNode<T> *t, void(*visit)(BSNode<T>&))const{
3     if(t!=NULL){
4         PostTraverse(t->lchild, visit);
5         PostTraverse(t->rchild, visit);
6         visit(*t);
7     }
8 }

平衡二叉树（AVL树）

　　平衡二叉树是由前苏联的两位数学家G.M.Adelse-Velskil和E.M.Landis提出，因此一般也称作AVL树，AVL树本质还是一棵二叉查找树，只是在其基础上增加了“平衡”的要求。所谓平衡是指，对AVL树的任意结点来说，其左子树与右子树的高度之差的绝对值不超过1，其中左子树与右子树的高度因子之差称为平衡因子。

　　如下所示，就是一棵由{1，2，3，4，5，7，8}构建的AVL树：

　　

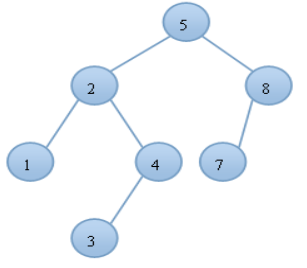
　　只要能随时保证每个结点平衡因子的绝对值不超过1，AVL的高度就始终能保持O(logn)级别，由于需要对每个结点都得到平衡因子，因此需要在树的结构中加入一个变量height来记录以当前结点为根结点的子树的高度。

AVL树的创建

　　AVL树的创建是基于二叉查找树的插入代码的基础上，增加平衡操作的。需要从插入的结点开始从下往上判断结点是否失衡，因此，需要在调用insert函数以后，更新当前子树的高度，并在这之后根据树型来进行相应的平衡操作。那么，怎么进行平衡操作呢？AVL树的插入是需要采取左旋或者右旋操作的，即，插入后，由于插入操作，导致某棵子树的高度超过了另一棵子树高度的2个结点高度，这样就破坏了树的平衡性，需要做出调整。

右旋操作

如下所示一棵简单的AVL树，对其进行插入操作以后：

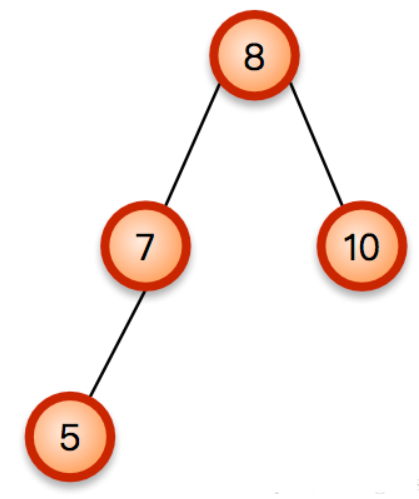
一棵简单的AVL树

变成了下图这样的AVL树：

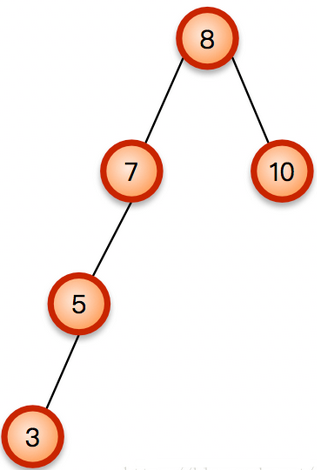
这样子就失衡了，所谓右旋操作，就是将这棵AVL树，从最靠近插入结点的失衡结点处，通过往右子树调整，使整棵树的每个结点的平衡因子变为正常，不如上图的树，离插入节点3最近的失衡结点是7，

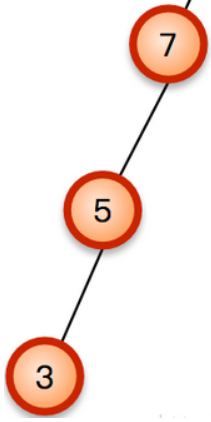
则可以通过下图所示的操作，来平衡二叉树，即调整整棵树平衡因子：

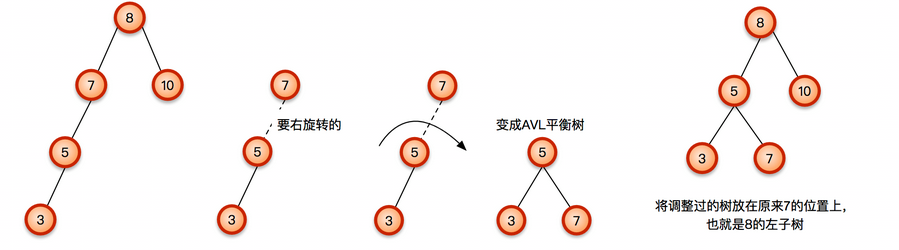
同样，左旋也与此类似。但是，如果5结点本身就有右结点，即如下所示：

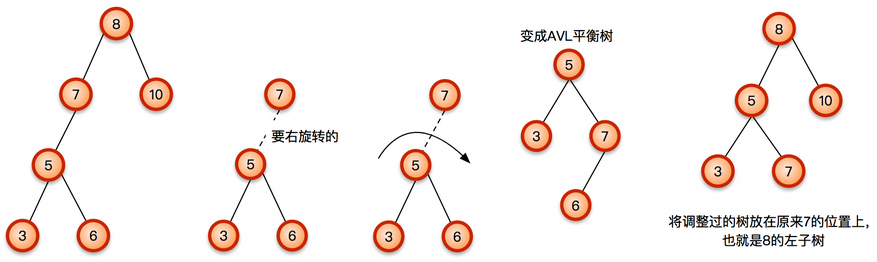
这样，在经过右旋操作以后，这棵树还是不平衡的，旋转后这棵树如下所示：

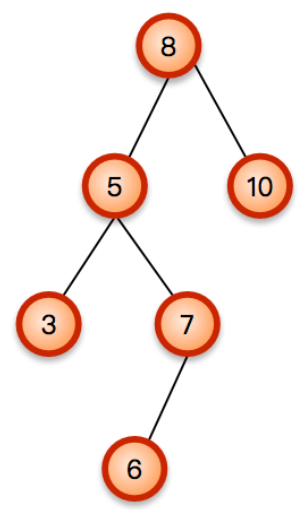
因此，还需要进行一次旋转，显然，继续右旋已经无法满足我们的需求，那么要如何进行操作，才能使这棵树回复平衡呢？（在后续中，会进行讲解）

左旋操作

左旋操作与右旋操作是类似的，都属于对子树的单旋转。

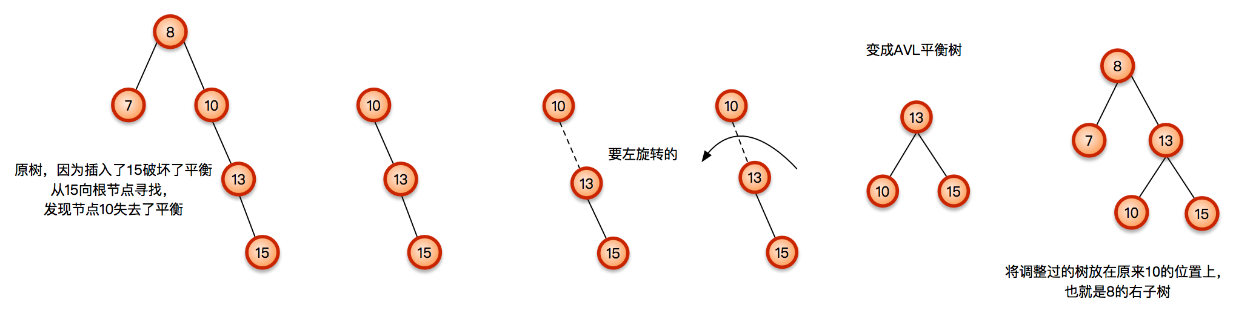
左旋与右旋一样，同样也存在这样的问题，如果该树的右子树的左结点存在，则单一通过左旋是做不到的，那么应该如何处理呢？

其实，以L和R来表示，插入结点的位置，有以下四种情况：

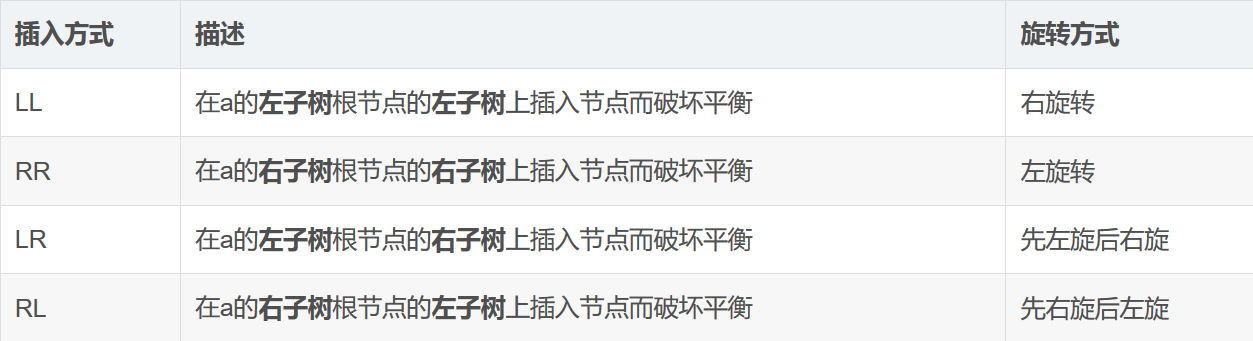
从上表可以看出，左旋和右旋两种情况中，左右结点若存在的话，就是上表中的RL和LR情况。则，只需要对两种情况分别按照上表采取相应的操作就可以解决，如下图所示：

LR型

RL型

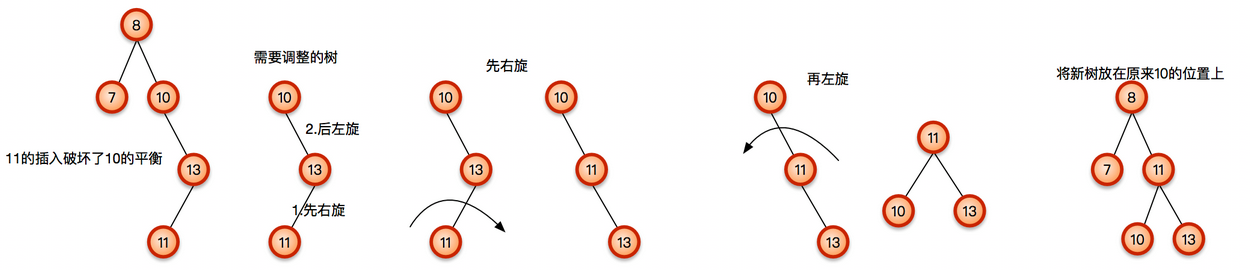
由此，就能实现AVL树的平衡，下面给出代码：

AVLTree.h

  1 #ifndef _AVLTREE_H_
  2 #define _AVLTREE_H_
  3 #include "C.h"
  4 #include "AVLNode.h"
  5 #include "Function.h"
  6
  7 typedef int T;
  8
  9 using namespace std;
 10
 11 template<typename T>
 12 class AVLTree{
 13 private:
 14     AVLNode<T> *root;
 15     Destroy(AVLNode<T> *t){
 16         if(t!=NULL){
 17             Destroy(t->lchild);
 18             Destroy(t->rchild);
 19             delete t;
 20             t = NULL;
 21         }
 22         return 0;
 23     }
 24 public:
 25     AVLTree(){
 26         root = NULL;
 27     }
 28     ~AVLTree(){
 29         Destroy(root);
 30     }
 31
 32     AVLNode<T>* newAVLNode(T x);    //创建新结点
 33     void Insert(AVLNode<T>* &t, T x);
 34     void createAVLTreeFromFile(ifstream &f);
 35     AVLNode<T>* Root()const;
 36     int AVLTreeDepth(AVLNode<T> *t)const;
 37     int getAVLTreeHeight(AVLNode<T>* t)const;   //获取当前结点的高度
 38     int getBalanceFactor(AVLNode<T>* t)const;   //计算当前结点的高度
 39     void updateAVLNodeHeight(AVLNode<T>* &t);
 40     T getElem(AVLNode<T>* t)const;
 41     bool getElemExist(AVLNode<T>* &t)const;
 42     void LeftRotation(AVLNode<T>* &t);
 43     void RightRotation(AVLNode<T>* &t);
 44     void PreOrderTraverse(AVLNode<T>* t, void(*visit)(AVLNode<T>&))const;
 45     void PostOrderTraverse(AVLNode<T>* t, void(*visit)(AVLNode<T>&))const;
 46 };
 47
 48 template<typename T>
 49 AVLNode<T>* AVLTree<T>::newAVLNode(T x){
 50     AVLNode<T>* avlnode = new AVLNode<T>;
 51     avlnode->data = x;
 52     avlnode->height = 1;
 53     avlnode->lchild = avlnode->rchild = NULL;
 54     return avlnode;
 55 }
 56
 57 template<typename T>
 58 void AVLTree<T>::Insert(AVLNode<T>* &t, T x){
 59     if(t==NULL){
 60         t = newAVLNode(x);
 61         return;
 62     }
 63     if(x==t->data){//结点已经存在，直接返回
 64         return;
 65     }
 66     if(x < t->data){
 67         Insert(t->lchild, x);
 68         updateAVLNodeHeight(t);
 69         if(getBalanceFactor(t)==2){
 70             if(getBalanceFactor(t->lchild)==1){
 71                 RightRotation(t);
 72             }
 73             else if(getBalanceFactor(t->lchild)==-1){
 74                 LeftRotation(t->lchild);
 75                 RightRotation(t);
 76             }
 77         }
 78     }
 79     else{
 80         Insert(t->rchild, x);   //值比当前结点大，往右子树插入
 81         updateAVLNodeHeight(t);     //更新树高
 82         if(getBalanceFactor(t)==-2){
 83             if(getBalanceFactor(t->rchild)==-1){ //RR型
 84                 LeftRotation(t);
 85             }
 86             else if(getBalanceFactor(t->rchild)==1){
 87                 RightRotation(t->rchild);
 88                 LeftRotation(t);
 89             }
 90         }
 91     }
 92 }
 93
 94 template<typename T>
 95 void AVLTree<T>::createAVLTreeFromFile(ifstream &f){
 96     T e;
 97     while(!f.eof()){
 98         InputFromFile(f, e);
 99         Insert(root, e);
100     }
101 }
102
103 template<typename T>
104 AVLNode<T>* AVLTree<T>::Root()const{
105     return root;
106 }
107
108 template<typename T>
109 int AVLTree<T>::AVLTreeDepth(AVLNode<T> *t)const{
110     int i,j;
111     if(t==NULL){
112         return 0;
113     }
114     else{
115         i = AVLTreeDepth(t->lchild);
116         j = AVLTreeDepth(t->rchild);
117     }
118     return i>j ? i+1 : j+1;
119 }
120
121 template<typename T>
122 int AVLTree<T>::getAVLTreeHeight(AVLNode<T>* t)const{
123     if(t==NULL){
124         return 0;
125     }
126     return t->height;
127 }
128
129 template<typename T>
130 int AVLTree<T>::getBalanceFactor(AVLNode<T>* t)const{
131     if(t==NULL){
132         return 0;
133     }
134     return getAVLTreeHeight(t->lchild) - getAVLTreeHeight(t->rchild);
135 }
136
137 template<typename T>
138 void AVLTree<T>::updateAVLNodeHeight(AVLNode<T>* &t){
139     t->height = max(getAVLTreeHeight(t->lchild), getAVLTreeHeight(t->rchild)) + 1;
140 }
141
142 template<typename T>
143 T AVLTree<T>::getElem(AVLNode<T>* t)const{
144     return t->data;
145 }
146
147 template<typename T>
148 bool AVLTree<T>::getElemExist(AVLNode<T>* &t)const{//判断当前结点是否为空
149     if(t!=NULL){
150         return true;
151     }
152     return false;
153 }
154
155 template<typename T>
156 void AVLTree<T>::LeftRotation(AVLNode<T>* &t){
157     AVLNode<T> *temp = t->rchild;
158     t->rchild = temp->lchild;
159     temp->lchild = t;
160     updateAVLNodeHeight(t);
161     updateAVLNodeHeight(temp);
162     t = temp;
163 }
164
165 template<typename T>
166 void AVLTree<T>::RightRotation(AVLNode<T>* &t){
167     AVLNode<T> *temp = t->lchild;
168     t->lchild = temp->rchild;
169     temp->rchild = t;
170     updateAVLNodeHeight(t);
171     updateAVLNodeHeight(temp);
172     t = temp;
173 }
174
175 template<typename T>
176 void AVLTree<T>::PreOrderTraverse(AVLNode<T>* t, void(*visit)(AVLNode<T>&))const{
177     if(t!=NULL){
178         visit(*t);
179         PreOrderTraverse(t->lchild, visit);
180         PreOrderTraverse(t->rchild, visit);
181     }
182 }
183
184 template<typename T>
185 void AVLTree<T>::PostOrderTraverse(AVLNode<T>* t, void(*visit)(AVLNode<T>&))const{
186     if(t!=NULL){
187         PostOrderTraverse(t->lchild, visit);
188         PostOrderTraverse(t->rchild, visit);
189         visit(*t);
190     }
191 }
192 #endif // _AVLTREE_H_

Function.h

 1 #ifndef _FUNCTION_H_
 2 #define _FUNCTION_H_
 3 #include "C.h"
 4 #include "AVLNode.h"
 5 #include "AVLTree.h"
 6
 7 typedef int T;
 8
 9 using namespace std;
10
11 bool InputFromFile(ifstream &f, T &e){
12     f>>e;
13     return f.good();
14 }
15
16 void visit(AVLNode<T> &t){
17     cout<<t.data<<" ";
18 }
19
20 #endif // _FUNCTION_H_

C.h

 1 #ifndef _C_H_
 2 #define _C_H_
 3 #include<iostream>
 4 #include<string>
 5 #include<stdio.h>
 6 #include<algorithm>
 7 #include<map>
 8 #include<math.h>
 9 #include<queue>
10 #include<stack>
11 #include<vector>
12 #include<fstream>
13 #include<assert.h>
14 #endif // _C_H_

AVLNode.h

 1 #ifndef _AVLNODE_H_
 2 #define _AVLNODE_H_
 3
 4 typedef int T;
 5
 6 template<typename T>
 7 struct AVLNode{
 8     int height;     //平衡因子
 9     T data;     //数据域
10     AVLNode<T> *lchild, *rchild;    //指针域
11 };
12 #endif // _AVLNODE_H_