一本通 一笔画问题 洛谷P1636 Einstein学画画

P1636 Einstein学画画

相信大家都玩过一笔画这种游戏吧，这其实算得上是我们能够接触到的比较常见的数学问题，有一个很知名的就是七桥问题

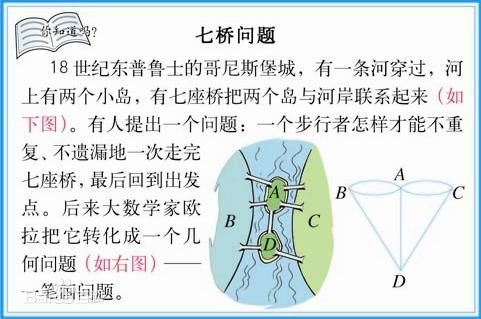
这个问题包括所有的一笔画问题都是在欧拉回路的涵盖范围内的，那么欧拉回路又是什么呢？

我们把一个这个桥化为无向图进行这样一个分析，除了起点以外，每一次当一个人由一座桥进入一块陆地（或点）时，他同时也由另一座桥离开此点。所以每行经一点时，计算两条边，从起点离开的线与最后回到始点的线亦计算两座桥，因此每一个陆地与其他陆地连接的桥数必为偶数。

读不懂没关系，多读几遍慢慢理解，我们把这个化简一下，就成了

对于无向图：

　　存在欧拉回路的条件：每个点的度都为偶数；

　　存在欧拉路的条件：有且只有两个点的度为一，且这两个点分别为起点和终点；

对于有向图：

　　存在欧拉回路的条件：每个点出度等于入度；

　　存在欧拉路的条件：存在一个点出度比入度多一作为起点，存在一点入度比出度多一作为终点，其余点出度等于入度；

你还觉得麻烦是吗，再化简一下

如果一个图能一笔画，那么叫做欧拉图，如果这个图最后能回到起点，那么叫做欧拉回路

定理一：存在欧拉路的条件：图是联通的，且只有2个奇点

定理二：存在欧拉回路的条件：图是联通的，且有0个奇点

那么我们看这个题,他其实就是考差了一个对图上所有点的遍历，我们把所有点进行遍历，把所有与其相连的边进行遍历，遍历完一个点之后，如果是奇点就加到计数器当中去，来看代码吧

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
using namespace std;
int n, m, graph[][], x, y,_count,sum;
int main()
{
    memset(graph, , sizeof(graph));
    scanf("%d%d", &n, &m);
    for (int i = ; i <= m; ++i)
    {
        scanf("%d%d", &x, &y);
        graph[x][y] = graph[y][x] = ;
    }
    for (int i = ; i <= n; ++i)
    {
        for (int j = ; j <= n; ++j)
        {
            if (graph[i][j] == )
                _count++;
        }
        if(_count%) sum++;
        _count=;
    }
    if(sum==)
    cout<<;
    else cout<<ceil(sum/2.0);
    return ;
}
/*
这道题就是一个简单的欧拉回路的模板，统计每个点的度数，如果每个点的度数都为偶数，那么就可以一笔画(因为每个点都有进有出)
否则统计度数为奇数的点的个数(记为num)
答案就是num/2(每次都把度数为奇数的点分别作为起点和终点)。
*/