bzoj2434阿狸的自动机

转载自 http://www.cnblogs.com/zj75211/p/6934976.html

●BZOJ 2434: [Noi2011]阿狸的打字机

 

●赘述题目

（题意就不赘述了）

●解法：

●我先想的一个比较暴力的方法（要TLE）：

（ac自动机）先求出last数组（参见刘汝佳的解释：last[j]：表示j节点沿着失配指针往回走时，遇到的下一个单词节点（即单词在此结束）的编号），然后对输入的编号为y的字符串的每一个位置进行递归寻找是否能连上x字符串的结束节点。（给出失败代码片段图，就不解释了）

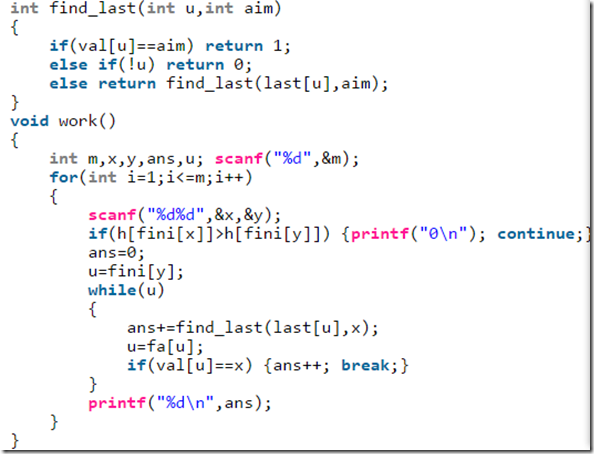
●正解：

（ac自动机）求出fail数组，然后以fail数组建树，如图

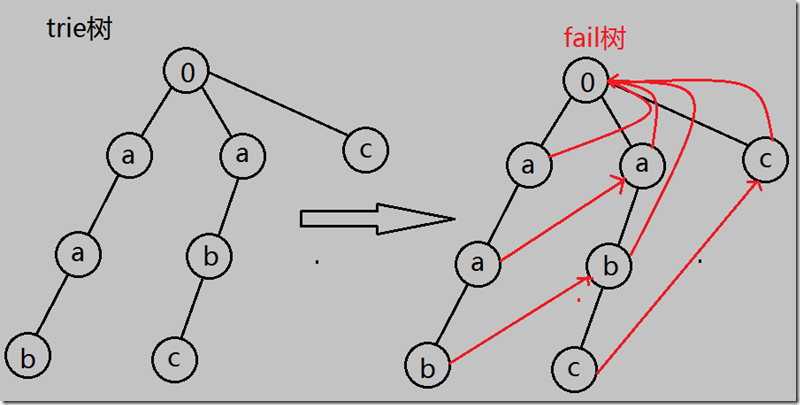
（看啊，红色的边和各点形成了另一棵树）

那么（看红树），若一个点在某个字符串结束节点的子树内，那么该字符串则出现在那个点所在的字符串里；如图中的a-b-c字符串和c字符串。

现在，我们若要求x字符串在y内出现了几次，就只需求以x的结束节点为根的子树内，有多少个节点是y字符串上的。

如何做呢？

将询问离线，y相同询问的弄在一起；

然后求出红树的dfs序（有点诡异，看代码）；

我们再遍历一遍输入的字符串：

对于输入的‘a’-‘z’，把对应的dfs序中其出现的位置的值加1，用树状数组维护；

对于输入的‘B’，现在的字符所对应的dfs序中的位置的值减1；

对于遇到的c个‘P’，我们不难发现，现在的树状树状维护的便是第c个字符串的每一个字符在dfs序中的位置的值所加1后的结果。接着便可用区间查询求出y==c的询问的答案。

那么上代码：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102

#include<cstdio> #include<cstring> #include<queue> #include<algorithm> #include<iostream> using namespace std; struct node{     int x,y; } q[100005]; struct edge{     int to,next; }e[200005]; int ch[100005][27]; int val[100005],fail[100005],fa[100005],fini[100005],l[100005],r[100005],ans[100005]; int head[100005],headq[100005],nxt[100005],lat[100005],c[150000]; char x[100005]; int cnt,pnt,ent=1,dnt,lx; int idx(char x) {return x-'a';} void modify(int u,int d) {for(int i=u;i<=dnt;i+=i&(-i)) c[i]+=d;} int query(int u) {int sum=0;for(int i=u;i;i-=i&(-i)) sum+=c[i]; return sum;} void add(int u,int v) {     e[ent]=(edge){v,head[u]};head[u]=ent++;     e[ent]=(edge){u,head[v]};head[v]=ent++; } void read_trie() {     int u=0;     for(int i=1;i<=lx;i++)     {         if(x[i]=='B') u=fa[u];         else if(x[i]=='P') val[u]=++pnt,fini[pnt]=u;         else         {             int c=idx(x[i]);             if(!ch[u][c]) ch[u][c]=++cnt,fa[ch[u][c]]=u;             u=ch[u][c];         }     } } void get_fail() {     queue<int> q;     for(int c=0;c<26;c++) {int u=ch[0][c]; if(u) q.push(u);}     while(!q.empty())     {         int r=q.front(); q.pop();         for(int c=0;c<26;c++)         {             if(!ch[r][c]) continue;             int u=ch[r][c];             q.push(u);             int v=fail[r];             while(v&&!ch[v][c]) v=fail[v];             fail[u]=ch[v][c];         }     } } //---------------------------------------------------------------------- void dfs_xu(int u,int fa) {     l[u]=++dnt;     for(int i=head[u];i;i=e[i].next) if(e[i].to!=fa) dfs_xu(e[i].to,u);     r[u]=dnt; } void work() {     int m; scanf("%d",&m);     for(int i=1;i<=m;i++)     {         scanf("%d%d",&q[i].x,&q[i].y);          nxt[i]=lat[q[i].y];         lat[q[i].y]=i;     }     for(int i=1;i<=cnt;i++) add(i,fail[i]);     dfs_xu(0,0);     int p=0,id=0;     for(int i=1;i<=lx;i++)     {         if (x[i]=='P')         {             id++;             for (int j=lat[id];j;j=nxt[j])             {                  int u=fini[q[j].x];                  ans[j]=query(r[u])-query(l[u]-1);              }          }          else if (x[i]=='B') modify(l[p],-1),p=fa[p];          else p=ch[p][idx(x[i])],modify(l[p],1);      }     for(int i=1;i<=m;i++) printf("%d\n",ans[i]); } int main() {     scanf("%s",x+1);     lx=strlen(x+1);     read_trie();     get_fail();     work();     return 0; }