mex （离散化+线段树）

Time Limit: 3000 ms   Memory Limit: 256 MB

Description

　　给你一个无限长的数组，初始的时候都为0，有3种操作：

　　操作1是把给定区间$[l,r]$设为1，

　　操作2是把给定区间$[l,r]$设为0，

　　操作3把给定区间$[l,r]$0,1反转。

　　一共n个操作，每次操作后要输出最小位置的0。

Input

　　第一行一个整数n，表示有n个操作

　　接下来n行，每行3个整数op,l,r表示一个操作

Output

　　共n行，一行一个整数表示答案

Sample Input	Sample Output
3 1 3 4 3 1 6 2 1 3	1 3 1

HINT

　　对于30%的数据$1\le n\le 10^3,1\le l\le r\le 10^{18}$

　　对于100%的数据$1\le n\le 10^5,1\le l\le r\le 10^{18}$

---

题解

　　离散化操作区间：

　　首先看到$1\le l\le r\le 10^{18}$的范围，第一反应离散化。

　   这题的离散化是非常讲究的，我们不能只把每个区间操作的两端点提取出来离散化（我就是这么干的，其他部分都是对的，结果眼睁睁地没法输出），因为这样无法考虑到区间之间的点，如下图：

　　

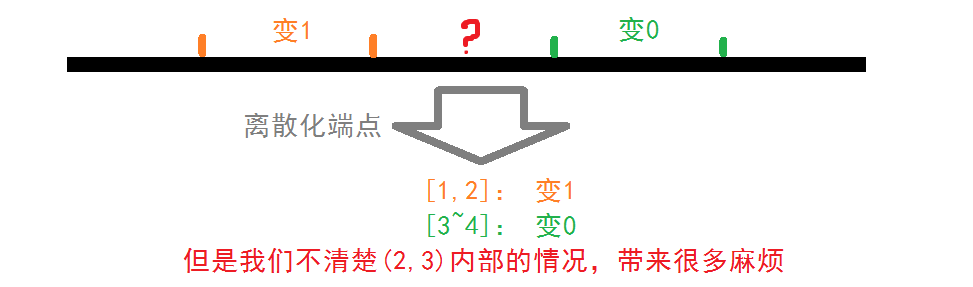
　　考虑到答案的位置，答案应该只可能出现在某一段操作区间右端点的右边一位，于是我们在离散一个操作区间$l,r$的同时，把$r+1$也离散化掉。操作并不涉及到$r+1$，仅仅是为了输出答案的正确和可行性。

　　实现修改操作：

　　　　看到熟悉的区间操作，当然要想想线段树啦。

　　　  这里采用两棵线段树的写法实现3种操作，当然也有一棵线段树搞定的写法。

　　　  两棵线段树$A,B$，都先按照离散化的规模建好，以离散化端点编号为索引。$A$记录$0$的信息，$B$记录$1$的信息。

　　　  线段树维护的信息是：$0$或$1$最左出现的位置。

　　　  第1个操作：将$A$的相应区间的信息清空（设置成最大值，因为不存在$0$了），将$B$的相应区间的信息填充（设置成区间的左端点位置），并打上清空或填充标记。日后记得下传。

　　　  第2个操作：与第1个操作完全相反。

　　     第3个操作：将$A$的相应区间节点和$B$的相应区间节点对调。

　　输出：

　　　　询问$A$中的最小值位置，输出离散化前的原值即可。可以发现这个点一定是某个区间的$r$再$+1$。

　　时间复杂度$O(n lg n)$，空间复杂度$O(n)$。

---

 #include <cstdio>
 #include <algorithm>
 #define min(a,b) (a<b?a:b)
 using namespace std;
 typedef long long ll;
 const int N=1e5+;
 ll INF=;
 int n,lshtot,opt[N][],total;
 ll inp[N][],lis[N*],minloc,maxloc,orival[N*];
 void lshAndfill(){
     sort(lis+,lis++lshtot);
     total=unique(lis+,lis++lshtot)-lis-;
     for(int i=;i<=total;i++) orival[i]=lis[i];
     orival[total+]=INF;
     for(int i=;i<=n;i++){
         opt[i][]=inp[i][];
         opt[i][]=lower_bound(lis+,lis++total,inp[i][])-lis;
         opt[i][]=lower_bound(lis+,lis++total,inp[i][])-lis;
     }
 }
 struct Seg{
     int cnt,root[],sz,ch[N*][],mark[N*];
     ll info[N*];
     void build(int Size){
         sz=Size;
         _build(root[],,sz,true);
         _build(root[],,sz,false);
     }
     void _build(int &u,int l,int r,bool isfill){
         if(!u) u=++cnt;
         mark[u]=-;
         if(l==r){
             if(isfill) info[u]=l;
             else info[u]=total+;
             return;
         }
         int mid=(l+r)>>;
         _build(ch[u][],l,mid,isfill);
         _build(ch[u][],mid+,r,isfill);
         pushup(u);
     }
     inline void pushup(int u){
         info[u]=min(info[ch[u][]],info[ch[u][]]);
     }
     inline void pushdown(int u,int l,int r){
         int lc=ch[u][],rc=ch[u][];
         if(mark[u]==-) return;
         mark[lc]=mark[rc]=mark[u];
         if(mark[u]==)
             info[lc]=info[rc]=total+;
         else{
             info[lc]=l;
             info[rc]=(l+r)/+;
         }
         mark[u]=-;
     }
     void setSeg(int flag,int l,int r){
         _setSeg(root[^flag],root[^flag],,sz,l,r);
     }
     void _setSeg(int u1,int u2,int l,int r,int L,int R){
         if(L<=l&&r<=R){
             info[u1]=total+;
             info[u2]=l;
             mark[u1]=; mark[u2]=;
             return;
         }
         pushdown(u1,l,r);
         pushdown(u2,l,r);
         int mid=(l+r)>>;
         if(L<=mid) _setSeg(ch[u1][],ch[u2][],l,mid,L,R);
         if(mid<R) _setSeg(ch[u1][],ch[u2][],mid+,r,L,R);
         pushup(u1);
         pushup(u2);
     }
     void swapSeg(int l,int r){_swapSeg(root[],root[],,sz,l,r);}
     void _swapSeg(int &u1,int &u2,int l,int r,int L,int R){
         if(L<=l&&r<=R){
             swap(u1,u2);
             return;
         }
         pushdown(u1,l,r);
         pushdown(u2,l,r);
         int mid=(l+r)>>;
         if(L<=mid) _swapSeg(ch[u1][],ch[u2][],l,mid,L,R);
         if(mid<R) _swapSeg(ch[u1][],ch[u2][],mid+,r,L,R);
         pushup(u1);
         pushup(u2);
     }
     inline ll getMin(int x){return info[root[x]];}
 }seg;
 int main(){
     scanf("%d",&n);
     minloc=-;
     for(int i=;i<=n;i++){
         scanf("%lld%lld%lld",&inp[i][],&inp[i][],&inp[i][]);
         lis[++lshtot]=inp[i][];
         lis[++lshtot]=inp[i][];
         lis[++lshtot]=inp[i][]+;
         if(minloc==-) minloc=min(inp[i][],inp[i][]);
         else minloc=min(minloc,min(inp[i][],inp[i][]));
     }
     lshAndfill();
     seg.build(total);
     for(int i=;i<=n;i++){
         if(minloc>){
             printf("1\n");
             continue;
         }
         if(opt[i][]<=)
             seg.setSeg(opt[i][]==,opt[i][],opt[i][]);
         else
             seg.swapSeg(opt[i][],opt[i][]);
         printf("%lld\n",orival[seg.getMin()]);
     }
     return ;
 }

奇妙代码