栈到CLR

提起栈想必会听到这样几个关键词：后进先出，先进后出，入栈，出栈。

栈这种数据结构，数组完全可以代替其功能。

但是存在即是真理，其目的就是避免暴漏不必要的操作。

如角色一样，不同的情景或者角色拥有不同的操作权限。

那我们来了解一下栈，栈是一种线性数据结构，并且只能从一端压入或者弹出 = 添加或者删除。

基于数组实现的栈是顺序栈，基于链表实现的链式栈。

接下来我们看一下.Net 是怎么实现栈的？

注释说的很明白：这是一个基于数组实现的顺序栈，其入栈复杂度O(n)，出栈复杂度为O(1)

    // A simple stack of objects.  Internally it is implemented as an array,
    // so Push can be O(n).  Pop is O(1).
    [DebuggerTypeProxy(typeof(System.Collections.Stack.StackDebugView))]
    [DebuggerDisplay("Count = {Count}")]
    [System.Runtime.InteropServices.ComVisible(true)]
    [Serializable]
    public class Stack : ICollection, ICloneable {
        private Object[] _array;     // Storage for stack elements
        [ContractPublicPropertyName("Count")]
        private int _size;           // Number of items in the stack.
        private int _version;        // Used to keep enumerator in sync w/ collection.
        [NonSerialized]
        private Object _syncRoot;

        private const int _defaultCapacity = ;

        public Stack() {
            _array = new Object[_defaultCapacity];
            _size = ;
            _version = ;
        }

入栈：我们也看到这个是基于数组并且支持的那个太扩容的栈，默认大小围为10，当存满之后就会两倍扩容。

        // Pushes an item to the top of the stack.
        //
        public virtual void Push(Object obj) {
            //Contract.Ensures(Count == Contract.OldValue(Count) + 1);
            if (_size == _array.Length) {
                Object[] newArray = new Object[*_array.Length];
                Array.Copy(_array, , newArray, , _size);
                _array = newArray;
            }
            _array[_size++] = obj;
            _version++;
        }

正如注释中提到的，入栈复杂度可以达到O(n)，出栈可以是O(1)　　

so Push can be O(n). Pop is O(1).　　

出栈Pop，复杂度为O(1)很好理解，

上面提到的动态栈是操作受限的数组，并且不会产生新的内存申请或者数据的搬移

我们只要是获取到最后一个，然后弹出（也就是删除）即可。

入栈Push，我们接下来分析一下出栈为什么复杂度为O(n):

前面有一篇《算法复杂度》 https://www.cnblogs.com/sunchong/p/9928293.html ，提到过：最好、最坏、平均

对于下面的入栈代码：

最好情况时间复杂度：不会有扩容和数据迁移，所以直接追加即可，复杂度为O(1)

最坏情况时间复杂度：需要扩容后并且搬移原来n个数据，然后再插入新的数据，复杂度为 O(n)

那么平均时间复杂度是多少呢？这里需要结合摊还分析法，进行复杂度分析。为什么这里要使用摊还分析法呢？

先耐心地看看其定义：

分析一个操作序列中所执行的所有操作的平均时间分析方法。

与一般的平均分析方法不同的是，它不涉及概率的分析，可以保证最坏情况下每个操作的平均性能。

总结一下摊还分析：执行的所有操作的平均时间，不扯概率。

一头雾水也不要紧，我们可以拿摊还分析来直接分析：

public virtual void Push(Object obj)
{
 //Contract.Ensures(Count == Contract.OldValue(Count) + 1);
     if (_size == _array.Length) 
　  {
      Object[] newArray = new Object[*_array.Length];
      Array.Copy(_array, , newArray, , _size);
       _array = newArray;
    }
    _array[_size++] = obj;
    _version++;
}

入栈的最坏情况复杂度是O(n),但是这个最坏情况时间复杂度是在n+1次插入的时候发生的，

剩下的n次是不需要扩容搬移数据，只是简单的入栈 O(1),所以均摊下来的复杂度是O(1)。

那么为什么微软的工程师在备注里写下push复杂度是O(n)？--这里指的是空间复杂度O(n)

栈这种数据结构的应用有很多场景，其中一种就是我们的线程栈或者说函数栈。

当开启一个线程时，Windows系统为每个线程分配一个1M大小的线程栈。分配这个用来干什么呢？

存储方法中的参数和变量。趁这个机会，我们了解一下CLR的内存模型。

首先对于C#代码时如何编程机器代码的呢？

c#代码 -> 编译器 -> IL -> JIT -> CPU指令

当一个线程执行到以下方法时会有什么操作呢？

这段代码也很简单，就是在Main方法中调用了GetCode()方法，其他的都是一些临时变量。

        static void Main(string[] args)
        {
            string parentCode = "PI001";
            string newCode = string.Empty;
            newCode = GetCode(parentCode);
        }

        static string GetCode(string sourceCode)
        {
            string currentMaxCode = "";
            string newCode = $"{sourceCode}{currentMaxCode}";
            return newCode;
        }

首先线程会分配1M内存用于存储临时变量和参数；

进入Main方法时，会将参数和返回地址依次压栈

static void Main(string[] args)

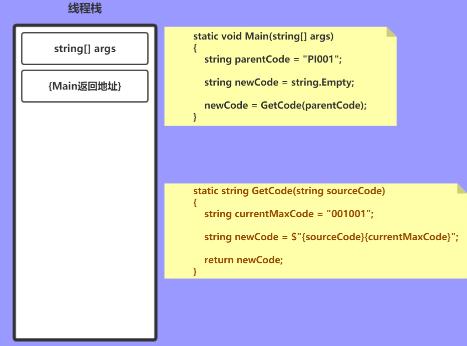
string parentCode = "PI001";
string newCode = string.Empty;

接下来开始进入到 GetCode() 方法，此时与之前一样压入参数和返回地址

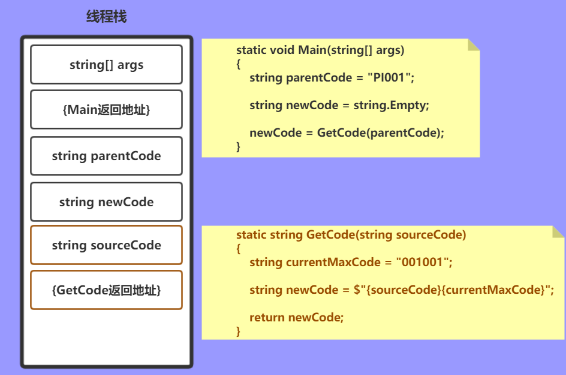
string currentMaxCode = "";
string newCode = $"{sourceCode}{currentMaxCode}";

既然说到了栈，那我们不得不再说一下托管堆，再来一段代码图解：

这是父类和子类的具体代码，可以略过此处。

     public class BaseProduct
     {
         public string GetCode()
         {
             string maxCode = "";
             return maxCode;
         }

         public virtual string Trim(string source)
         {
             return source.Trim();
         }
     }

     public class Product : BaseProduct
     {
         private static string _type="PI";

         public override string Trim(string source)
         {
             return source.Replace(" ", string.Empty);
         }

         public static string GetNewCode(string parentCode)
         {
             string currentMaxCode = "";
             string newCode = $"{parentCode}{currentMaxCode}";
             return newCode;

         }
     }

我们隐藏这些方法的具体实现，只预览他们的之间的关系：

接下来，线程即将进入到下面的这个方法：

        void GetProduct()
        {
            BaseProduct p;
            string sourceCode;
            p = new Product();
            sourceCode = p.GetCode();
            sourceCode = Product.GetNewCode(sourceCode);
        }

JIT在编译到此方法前会注意到这个方法所有的引用类型，

并向CLR发出通知，加载程序集，在托管对中创建相关的类型对象数据结构。

这也就是我们所能理解的静态字段为什么不是在实例化的时候创建，

而是在这个类型创建的时候就一直存在。

这其实就是两个概念，静态资源是属于类结构的，而实例资源时属于实例本身。

下面的图忽略String类型，因为String类型是常用类型可能在之前就已经创建好了，

类型对象包括：对象指针、同步块索引、静态资源、方法表，像下面这样：

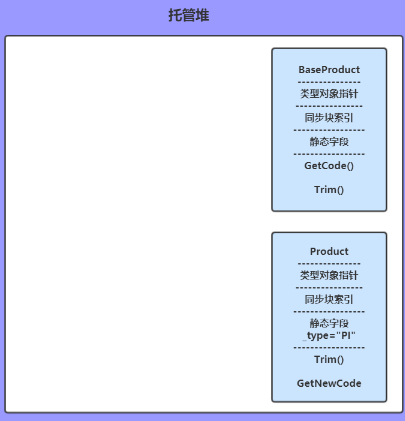
BaseProduct p;
string sourceCode;

方法变量入栈，并且引用类型初始化为null

p = new Product();

实例化Product ，托管堆创建Product对象，并将这个对象的指针指向Product类型。

将线程栈中的变量p指针，指向新创建的Product对象。

sourceCode = p.GetCode();

JIT找到这个变量p的Product对象，再找到对应的Product类型，表中找到此方法GetCode()；

当然这个方法实际是父类的方法，所以JIT会一直向上找，直到找到为止。

图中是个虚拟路线，计算结果赋值给 string sourceCode

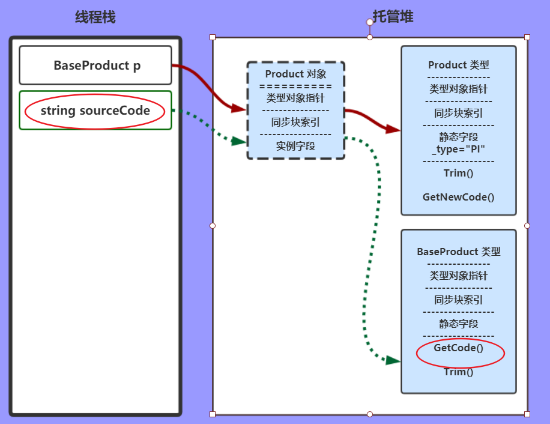
sourceCode = Product.GetNewCode(sourceCode);

和上一步类似，只不过这次是调用的静态方法。发出类型Product，静态方法是GetNewCode()

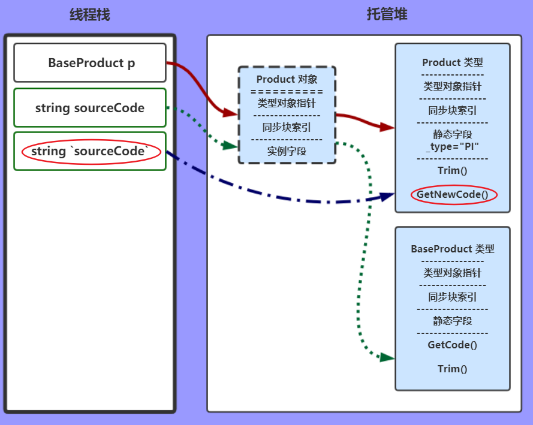
以上内容就是 JIT、CLR、线程栈、托管堆的一些运行时关系。

本文链接：https://www.cnblogs.com/sunchong/p/10011657.html，欢迎转载，如有不对的地方希望指正。

我们部门运营的公众号，里面有很多技术文章和最新热点，欢迎关注：