Ceva定理的四种证明方法

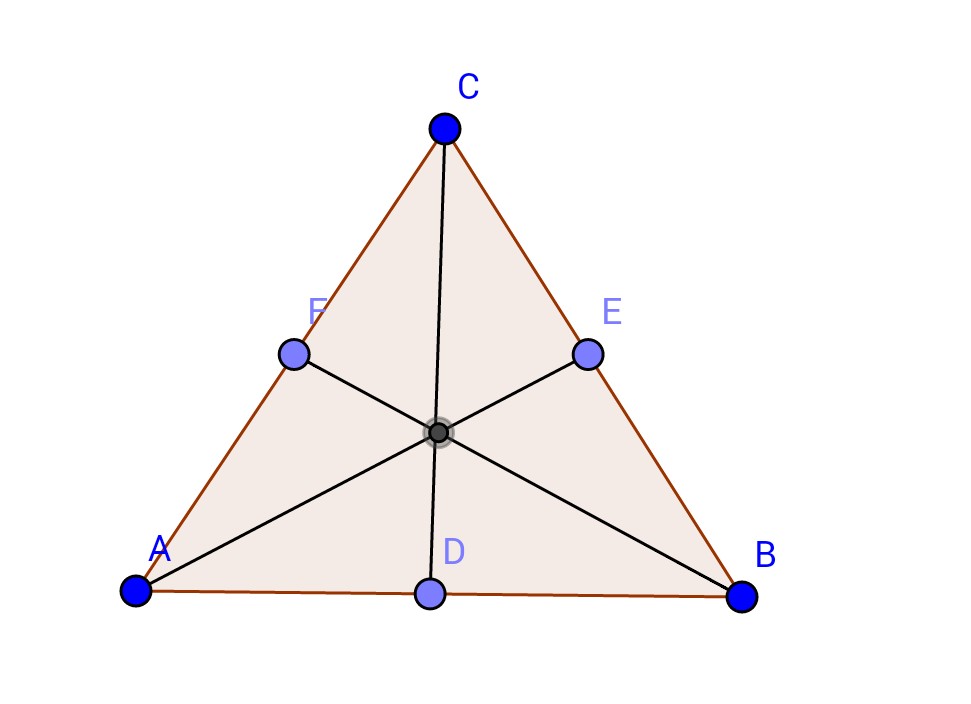
${\color{Teal} {Ceva定理}}$设$D、E、F$依次为三角形ABC的边$AB、BC、CA$的内点，记

$λ$=(A,B,D),$μ$=(B,C,E),$v$=(C,A,F)

求证:三条线段$AE、BF、CD$交于一点的充要条件是$λμv$=1

$\textbf{法一(向量法)}$

pf:

因为$$λ=(A,B,D)$$所以$$λ=\frac{AD}{DB}$$所以$$\overrightarrow {AD}=\frac{λ}{1+λ}\overrightarrow {AB}$$

同理$$\overrightarrow {BE}=\frac{μ}{1+μ}\overrightarrow {BC}$$ $$\overrightarrow {CF}=\frac{v}{1+v} \overrightarrow {CA}$$

$$\overrightarrow {CD}=\overrightarrow {CA}+\overrightarrow {AD}=\frac{1}{1+λ}\overrightarrow {CA}+\frac{λ}{1+λ}\overrightarrow {CB}$$

设CD、AE交于点O，令$\overrightarrow {CO}=α\overrightarrow {CD},\overrightarrow {AO}=β\overrightarrow {AE}$

$$\overrightarrow {CO}=\overrightarrow {BO}-\overrightarrow {BC}=\frac{α}{1+λ}\overrightarrow {CA}+\frac{αλ}{1+λ}\overrightarrow {CB}$$

$$\overrightarrow {BO}=\frac{α}{1+λ}\overrightarrow {CA}+\frac{αλ-λ-1}{1+λ}\overrightarrow {CB}$$

$$\overrightarrow {AE}=\overrightarrow {AB}+\overrightarrow {BE}=-\overrightarrow {CA}+\frac{1}{1+μ}\overrightarrow {CB}$$

$$\overrightarrow {AO}=\overrightarrow {BO}-\overrightarrow {BA}=β(\frac{1}{1+μ}\overrightarrow {CB}-\overrightarrow {CA})$$

所以$$\overrightarrow {BO}=(1-β)\overrightarrow {CA}+\frac{β-1-μ}{1+μ}\overrightarrow {BC}$$

由此我们得到$$\frac{α}{1+λ}=1+β$$ $$\frac{αλ-λ-1}{1+λ}=\frac{β-μ-1}{1+μ}$$

所以$$α=\frac{1+λ}{1+λ+λμ}$$ $$β=\frac{λ+μλ}{1+λ+μλ}$$

所以$$\overrightarrow {BO}=\frac{1}{1+λ+λμ}[\overrightarrow {CA}-(1+μλ)\overrightarrow {CB}]$$

$$\overrightarrow {BF}=\overrightarrow {BC}+\overrightarrow {CF}=\frac{1}{1+v}[v\overrightarrow {CA}-(1+v)\overrightarrow {CB}]$$

充分性证明

O在BF上，则 $$\frac{1}{v}=\frac{1+λμ}{1+v}$$ 即$$λμv=1$$

必要性证明

已知$λμv$=1

所以$$\overrightarrow {BF}=\frac{v(1+λ+λμ)}{1+v}\overrightarrow {BO}$$

所以$B、O、F$三点共线

$\textbf{法二:坐标法}$

在平面仿射坐标系$[A,\overrightarrow {AD},\overrightarrow {AC}]$中

得$B:(\frac{1+λ}{λ},0),C(0,1),D(1,D)，E:(\frac{1+λ}{λ(1+μ)},\frac{μ}{1+μ}),F:(0,\frac{1}{1+v})$

设O点坐标为$(\frac{(1+λ)x}{λ(1+μ)},\frac{μx}{1+μ})$

由$D、C、O$三点共线知$$\frac{(1+λ)x}{λ(1+μ)}+\frac{μx}{1+μ}=1$$

所以$$x=\frac{λ(1+μ)}{1+λ+λμ}$$ 所以O点坐标为$(\frac{1+λ}{1+λ+λμ},\frac{λμ}{1+λ+λμ})$

$B、O、F$共线等价于$$\begin{vmatrix} \frac{1+λ}{λ}& 0& 1\\ 0& \frac{1}{1+v}& 1\\ \frac{1+λ}{1+λ+λμ}& \frac{λμ}{1+λ+λμ} & 1 \end{vmatrix}=0$$ 即$$(1+λ)(1-λμv)=0$$ 即$$λμv=1$$

${\color{Blue} 注}$

当然如果建立仿射空间坐标系

$$C(1,0,0)、A(0,1,0)、B(0,0,1)$$

$$D(0,0,λ)、E(μ,0,1)、F(1,v,0)$$

则$$\overrightarrow {CD}=(0,λ,-1)$$ $$\overrightarrow {AE}=(-1,0,μ)$$ $$\overrightarrow {BF}=(v,-1,0)$$ 若$CD、AE、BF$三点共线于点O

则$$\begin{vmatrix} 0& λ& -1\\ -1& 0& μ\\ v& -1& 0 \end{vmatrix}=0$$ 即$$λμv-1=0$$ $$λμv=1$$

$\textbf{法三(梅氏定理)}$

对于$△CAD$和截线$FOB$

由梅氏定理得 $$\frac{AB}{BD} \frac{DO}{OC} \frac{CF}{FA}=-1$$ 同理可得$$\frac{BE}{EC} \frac{OC}{OD} \frac{DA}{AB}=-1$$ 两式相乘$$\frac{AD}{BD} \frac{BE}{EC} \frac{CD}{FA}=1$$ 即$$λμv=1$$

$\textbf{法四(面积比)}$

设$S_{△AOC}=S_{1},S_{△AOB}=S_{2},S_{△BOC}=S_{3}$

则$$\frac{CF}{AF}=\frac{S_{3}}{S_{2}}$$

$$\frac{AD}{BD}=\frac{S_{1}}{S_{3}}$$

$$\frac{BE}{EC}=\frac{S_{2}}{S_{1}}$$

三式相乘得 $$\frac{CF}{AF} \frac{AD}{BD}  \frac{BE}{EC}=1$$

即$$λμv=1$$