含隐变量模型求解——EM算法

1 EM算法的引入
1.1 EM算法
1.2 EM算法的导出
2 EM算法的收敛性
3EM算法在高斯混合模型的应用
3.1 高斯混合模型Gaussian misture model
3.2 GMM中参数估计的EM算法
4 EM推广
4.1 F函数的极大—极大算法

期望极大值算法（expectation maximizition algorithm，EM）。是一种迭代算法，1977年由Dempster总结提出，用于含有隐变量（hidden variable）的概率模型参数的极大似然估计或极大后验估计。EM算法分为两步，E步：求期望，M步：求极大值。

1 EM算法的引入

概率模型有时既含有观测变量(observable variable)，又含有隐变量或潜在变量（latent variable），如果仅有观测变量，那么给定数据就能用极大似然估计或贝叶斯估计来估计model参数；但是当模型含有隐变量时，需要一种含有隐变量的概率模型参数估计的极大似然方法估计——EM算法

1.1 EM算法

这里有一个三硬币模型，三个硬币A，B，C。正面出现的概率是π，p，q；只有当A硬币掷出后得到正面才会掷硬币B，否则C，但是独立n次后，只能观察到最后的结果，却看不到执行过程中A是什么情况，最后的结果是B还是C的。因此，



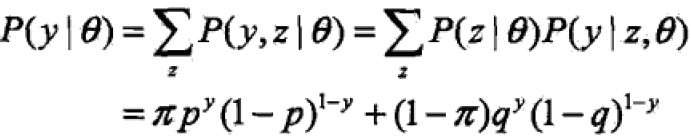
各个参数含义



观测数据的极大似然估计是：



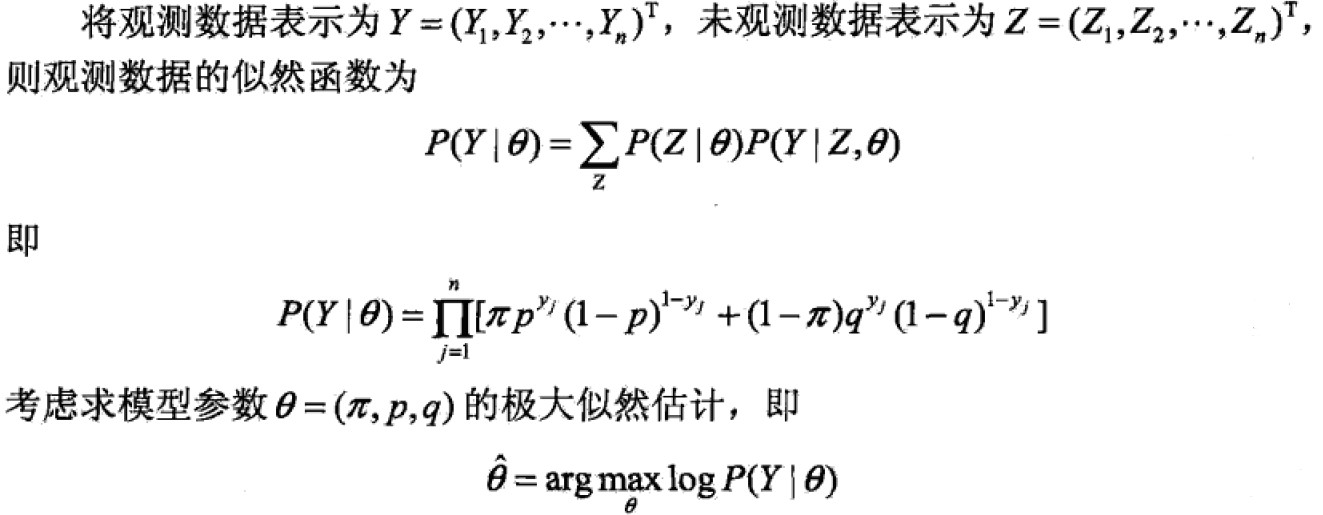
这个问题没有解析解，只能使用EM方法迭代求解。



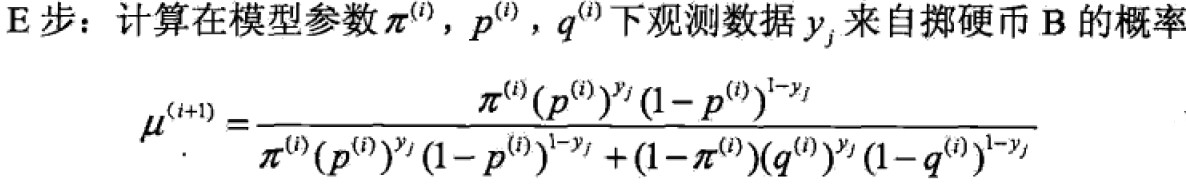
E步B的概率是一个条件概率，y取值为1,0.

M步：模型参数估计值



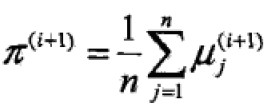
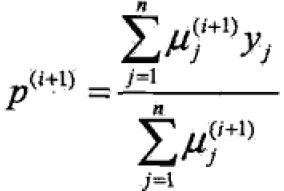
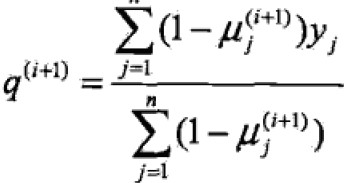
EM算法受初值影响较大。

一般地，Y表示观测数据，Z表示隐变量，Y+Z表示完全数据（complete data），Y叫做不完全数据（incomplete data）。假设给定观测数据Y其概率分布为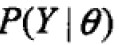，不完全数据Y的似然函数为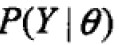，对数似然函数为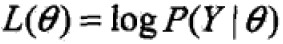，假设Y，Z联合概率分布为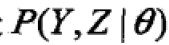，对数似然函数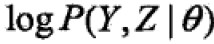，EM算法就是通过迭代求L的极大似然估计。

EM算法：





Q函数：EM算法的核心，是完全观测数据对数似然函数关于给定观测数据Y和当前参数θi对未观测数据Z的条件概率分布的期望：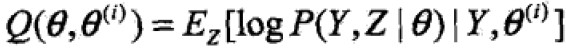

步骤1：参数的 初值可以任意选择，但是EM算法对参数初值十分敏感；

步骤2：求Q(θ，θi)第一个变元表示极大化的参数，第二个变元表示参数的当前估计值。每次迭代实际上再求Q函数及其极大。

步骤3：M步求Q的极大化，得到θi+1，完成一次迭代。

步骤4：给出停止条件，对较小的整数，满足入校条件则停止迭代。

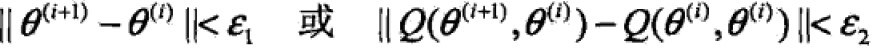
1.2 EM算法的导出

通过近似求解观测数据的对数似然函数的极大化问题来推导出EM算法的正确性。

问题是含有隐变量的概率模型，目标是极大化观测数据（不完全数据）Y关于θ的对数似然函数，即极大化，

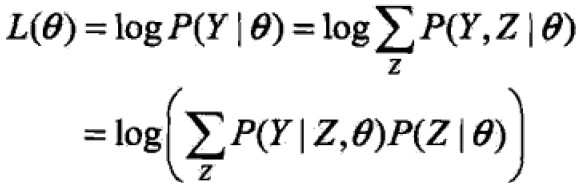困难点在于未观测数据和积分（求和）。

其实，EM算法是通过迭代逐步近似极大化L(θ)的。每次都希望最新的估计上跟上次的估计值大，来逐步达到极大值。



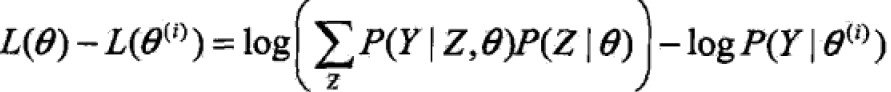
利用Jensen不等式得到下界：



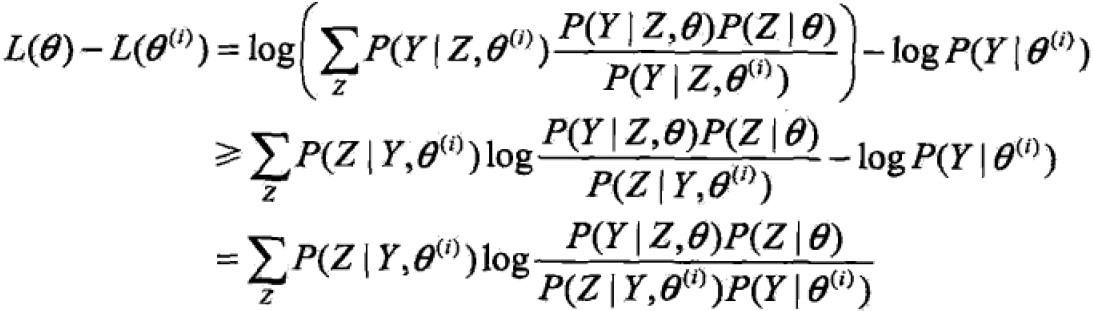
令



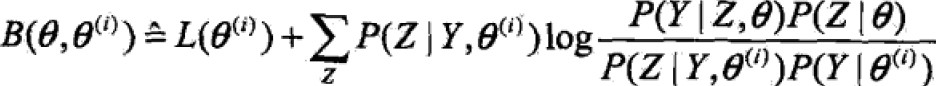
则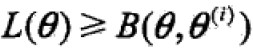，得到L的一个下界B函数，且可以发现，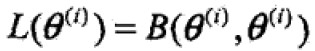

任何可以让B增大的θ也可以使得L增大，因此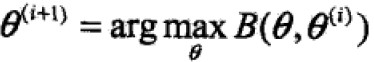，具体表达式化简（省略与θ无关的项）：



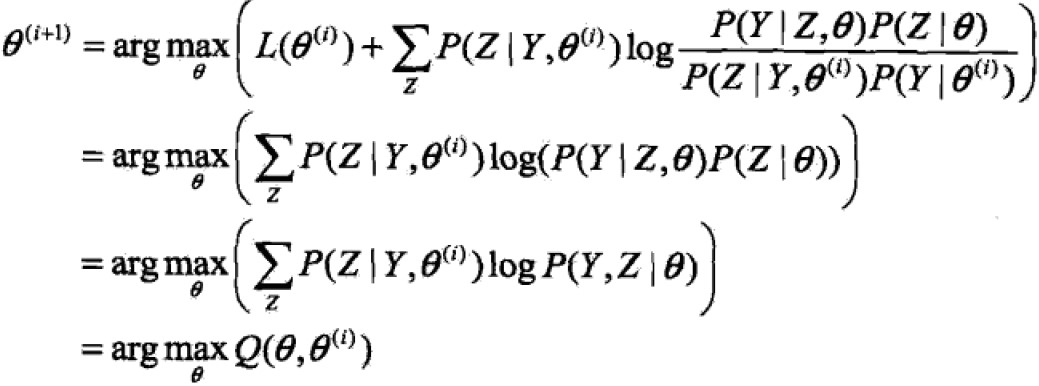
因此EM算法是通过不断求解下界的极大化来求解对数似然函数极大化的算法。

---

EM算法因为能够求解包含隐变量的概率模型，因此可用于生成模型的非监督学习，认为联合概率密度为P(X,Y)，X为观测数据，Y为未观测数据。

---

2 EM算法的收敛性

EM算法能否收敛，是否能收敛到全局最优？

两个定理：







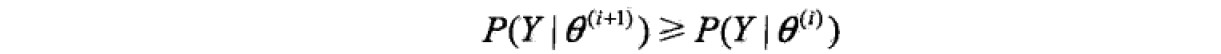
注意：定理只能保证参数估计序列收敛到对数似然函数序列的稳定点，不能保证收敛到极大值点，所以初值选择十分重要。通常的做法是选取几个不同的初值进行迭代，然后对得到的各个估计值加以比较，从中选择最好的。

3 EM算法在高斯混合模型的应用

3.1 高斯混合模型Gaussian misture model

GMM的形式：

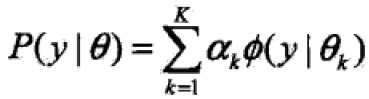，其中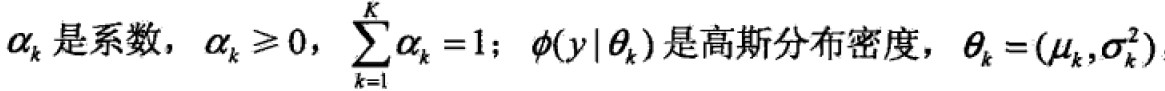

即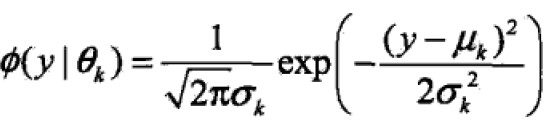，称为第k个分模型。

3.2 GMM中参数估计的EM算法

假设观测数据y1,y2,y3,…,yN由GMM生成

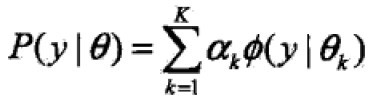其中，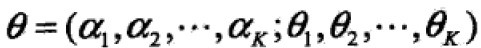

用EM算法估计参数θ。

1. 明确隐变量，写出完全数据的对数似然函数
   
   观测数据的产生：依照概率αk选择第k个高斯分布模型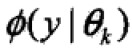；然后依照第k个分模型概率分布生成观测数据yj。这是观测数据是已知的，而反映观测数据yj的第k个分模型的数据是未知的，以隐变量γjk表示，定义如下：
   
   j=1,2,…,N;k=1,2,…,K，γ是0-1随机变量
   
   那么完全数据是：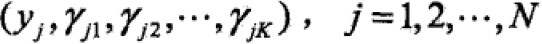
   
   完全数据似然函数是
   
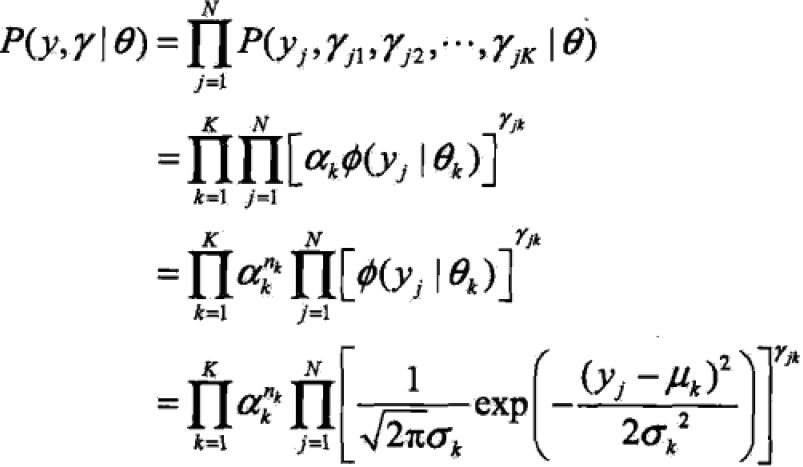   其中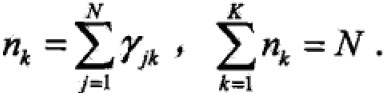，k的连乘不是很理解

对数化：

1. EM算法的E步：确定Q函数
   
   ，
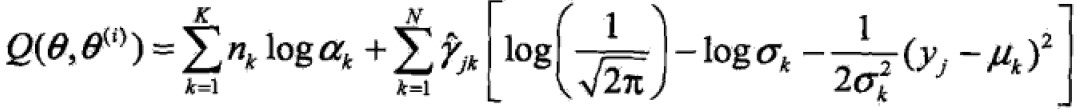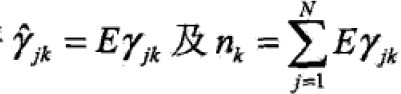
2. 确定M步
   
   
   
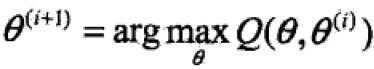
   求偏导为0推出：
   
   
   
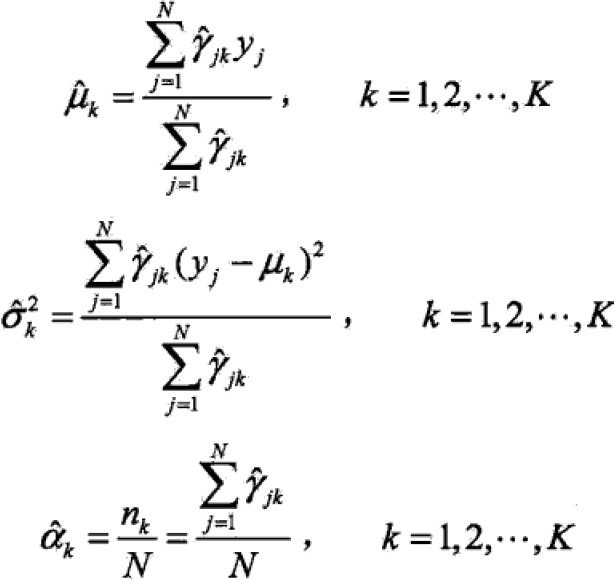
   算法：
   
   

4 EM推广

EM算法可以解释为F函数（F function）的极大—极大算法（maximization maximization algorithm），基于这个解释有若干变形，如，广义期望极大（generalized expectation maximization，GEM）算法。

4.1 F函数的极大—极大算法

F函数定义：



引理1：



引理2：



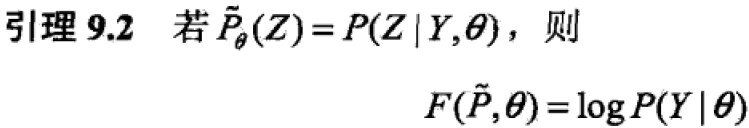
。。。未完待续。。。

推荐链接：http://blog.csdn.net/qq_20602929/article/details/51424292

总结：

EM算法是一种求解含有隐变量的概率模型参数的算法，这里主要根据《统计学习方法》介绍了EM算法及其推广和应用，主要的是理解，EM算法的E，M步，以及Q函数的构造方法，这是本质的东西。