B树(B-树)

1.基本概念:

M定义为树的高度，也叫阶，就是树的深度；

(1).B树又称为多路平衡查找树。

(2).根节点至少有两个子节点。

(3).除根节点以外的非叶子节点的儿子树为[M/2,M]。

(4).每个节点存放至少M/2 - 1 (向上取整) 和 至多 M-1个关键字。

(5).非叶子节点的关键字个数 = 指向儿子的指针个数 - 1。

(6).非叶子节点的关键字： K[1], K[2],...,K[M-1]; 且 K[i] < K[i + 1]。

(7).非叶子节点的指针 ： P[1],P[2],....P[M],其中P[1]指向关键字小于K[1]

P[M]指向关键字及其子树的值大于K[M-1]的值 。

(8).所有叶子节点位于同一层。

2.B-树的查找：

B-树的查找过程：根据给定值查找节点和在节点的关键字中进行查找交叉进行。首先从根节点开始重复如下过程：

若比节点的第一个关键字小，则查找在该节点第一个指针指向的节点进行，若等于节点中某个关键字，则查找成功；若在两个关键字之间，则查找在他们之间的指针指向的节点进行；若比该节点所有的关键字打，则查找在该节点最后一个指针指向的节点进行；若查找已经到达某个叶子节点，则说明给定值对应的数据记录不存在，查找失败。

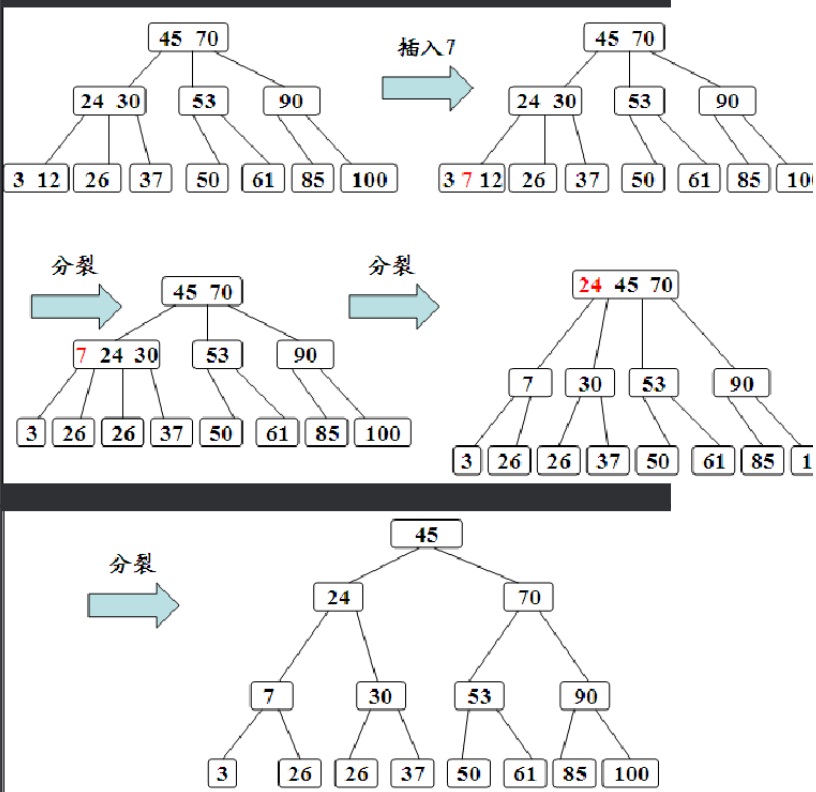
3.B-树的插入：

插入的过程分两步完成；

（1）利用前面的B-树的查找算法查找关键字的插入位置，若找到，则说明该关键字已经存在，直接返回。

（2）判断该节点是否还有空位置，即判断该节点的关键字总数是否小于M-1。若满足，则说明该节点还有空位置，直接把关键字K插入到该节点的合适位置上，若不满足，说明该节点已经没有空位置，需要把节点分成两个。

分裂的方法是：生成一个新节点。把原来节点上的关键字和K按照升序排序后，从中间位置把关键字分成两部分。左部分所含关键字放在旧节点中，右部分所含关键字放在新节点中，中间位置的关键字连同新节点的存储位置插入到父节点中。如果父节点的关键字个数也超过M-1则要再进行分裂，再往上插。直至这个过程传到根节点为止。

4.B_树的删除

在B-树上删除关键字K的过程分两步完成：

（1）利用前面的B-树的查找算法找出改关键字所在的节点。然后根据K所在节点是否为叶子节点有不同的处理方法；

（2）若该节点为非叶子节点，且被删除关键字为该节点中的第i个关键字key[i],则可从指针son[i]所指的子树中找出最小关键字Y，代替key[i]的位置，然后再叶子节点中删除Y。

因此，把在非叶子节点删除关键字K的问题就变成了删除叶子节点中的关键字问题了。

在B-树叶子节点上删除一个关键字的方法是

　　首先将要删除的关键字K直接从该叶子节点中删除。然后根据不同情况分别作相应的处理，共有三种可能情况：

（1）如果被删除关键字所在节点的原关键字个数n>=ceil(m/2),说明删除该关键字后该节点仍然满足B-树的蒂尼。这种情况最简单。

（2）如果被删除关键字所在节点的关键字个数n等于ceil(m/2) -1,说明删除该关键字后该节点不满足B-树的定义，需要调整。

　　调整的过程：如果其左右兄弟节点中右“多余”的关键字，即与该节点相邻的右（左）兄弟节点中的关键字数目大于ceil(m/2)-1。则可将右（左）兄弟节点中最小（大）关键字上移至双亲节点。而将双亲节点中小（大）于该上移关键字的关键字下移至被删关键字所在节点中。

（3）如果左右兄弟节点中没有“多余”的关键字，即与该节点相邻的右（左）兄弟节点中的关键字数目均等于ceil(m/2) - 1。这种情况比较复杂，需要把要删除关键字的节点与其左（或右）兄弟节点以及双亲节点中分割二者的关键字合并成一个节点，即在删除关键字后，该节点中剩余的关键字加指针，加上双亲节点中的关键字Ki一起，合并到Ai（是双亲节点指向该删除关键字节点的左(右）兄弟节点的指针）所指的兄弟节点中去。如果因此使双亲节点中关键字个数小于ceil(m/2) -1,则对此双亲节点做同样处理。以致于可能直到对根节点做这样的处理而使整个树减少一层。

总之，设所删关键字为非叶子节点中的Ki,则可以指针Ai所指子树中的最小关键字Y代替Ki，然后再相应节点中删除Y。对任意关键字的删除都可以转换为对最下层关键字的删除。

参考文献：http://www.cnblogs.com/oldhorse/archive/2009/11/16/1604009.html

　　　　　https://wenku.baidu.com/view/387c4d6c5727a5e9856a6186.html