洛谷 P2822 组合数问题

题目描述

组合数C_n^mC​n​m​​表示的是从n个物品中选出m个物品的方案数。举个例子，从（1,2,3) 三个物品中选择两个物品可以有（1,2),(1,3),(2,3)这三种选择方法。根据组合数的定 义，我们可以给出计算组合数的一般公式：

C_n^m=\frac{n!}{m!(n - m)!}C​n​m​​=​m!(n−m)!​​n!​​

其中n! = 1 × 2 × · · · × n

小葱想知道如果给定n,m和k，对于所有的0 <= i <= n，0 <= j <= min(i,m)有多少对 (i,j)满足C_i^jC​i​j​​是k的倍数。

输入输出格式

输入格式：

第一行有两个整数t,k，其中t代表该测试点总共有多少组测试数据，k的意义见 【问题描述】。

接下来t行每行两个整数n,m，其中n,m的意义见【问题描述】。

输出格式：

t行，每行一个整数代表答案。

输入输出样例

输入样例#1：

1 2
3 3

输出样例#1：

1

输入样例#2：

2 5
4 5
6 7

输出样例#2：

0
7

说明

【样例1说明】

在所有可能的情况中，只有C_2^1 = 2C​2​1​​=2是2的倍数。

【子任务】

题解：杨辉三角求组合数+前缀和

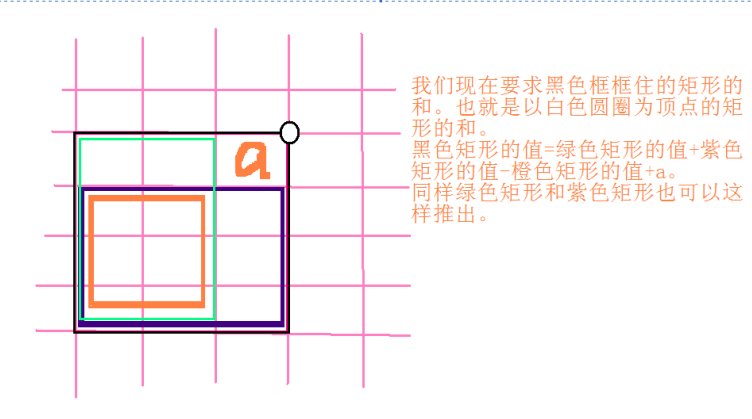
代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int c[][],sum[][];
int t,k,n,m;

int main(){
    scanf("%d%d",&t,&k);
    for(int i=;i<=;i++){
        for(int j=;j<=i;j++){
            if(j==)c[i][j]=;
            else if(i==j)c[i][j]=;
            else c[i][j]=(c[i-][j]%k+c[i-][j-]%k)%k;
        }
    }
    sum[][]=c[][]==?:;
    for(int i=;i<=;i++){
        for(int j=;j<=;j++){
            sum[i][j]=sum[i-][j]+sum[i][j-]-sum[i-][j-];
            if(c[i][j]==&&i>=j)sum[i][j]++;
        }
    }
    while(t--){
        scanf("%d%d",&n,&m);
        printf("%d\n",sum[n][m]);
    }
    return ;
}