Complete Binary Search Tree

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
• Both the left and right subtrees must also be binary search trees.

  A Complete Binary Tree (CBT) is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.

  Now given a sequence of distinct non-negative integer keys, a unique BST can be constructed if it is required that the tree must also be a CBT. You are supposed to output the level order traversal sequence of this BST.

  Input Specification:

  Each input file contains one test case. For each case, the first line contains a positive integer N (≤). Then N distinct non-negative integer keys are given in the next line. All the numbers in a line are separated by a space and are no greater than 2000.

  Output Specification:

  For each test case, print in one line the level order traversal sequence of the corresponding complete binary search tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.

  Sample Input:

  Sample Output:

 #include <cstdio>
 #include <math.h>
 #include <algorithm> 

 using namespace std;

 int a[];
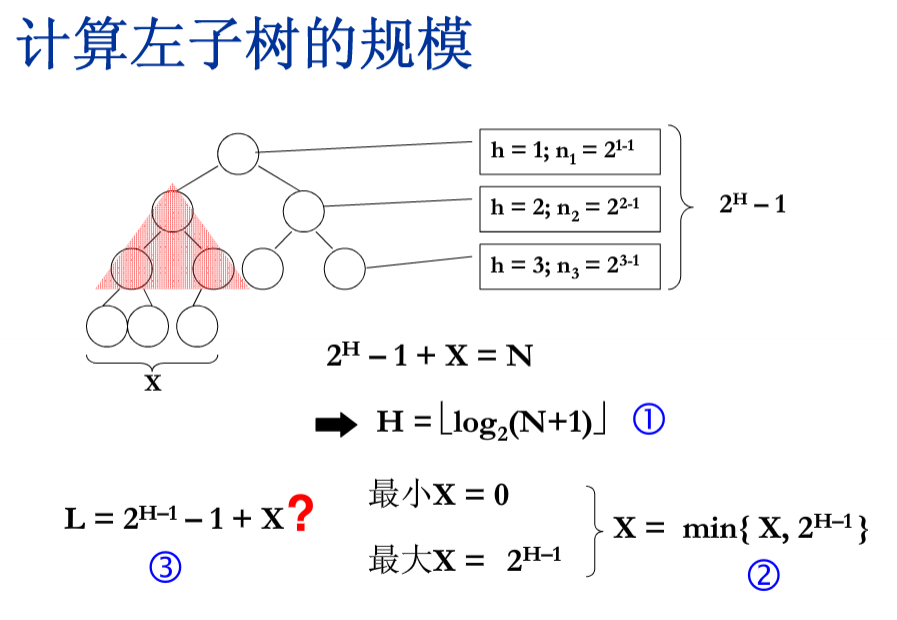
 int T[];

 int GetLeftLength(int n)
 {
     int H=log(n+)/log();
     int X=n+-pow(,H);
     if(X>pow(,H-))
         X=pow(,H-);
     int L=pow(,H-)-+X;
     return L;
 }

 void solve(int ALeft,int ARight,int TRoot)
 {
     int n=ARight-ALeft+;
     if(n==) return;
     int L=GetLeftLength(n);
     T[TRoot]=a[ALeft+L];
     int LeftTRoot=TRoot*+;
     int RightTRoot=LeftTRoot+;
     solve(ALeft,ALeft+L-,LeftTRoot);
     solve(ALeft+L+,ARight,RightTRoot);
 }

 int main()
 {
     int n;
     scanf("%d",&n);
     for(int i=;i<n;i++)
     {
         scanf("%d",&a[i]);
     }
     sort(a,a+n);
     solve(,n-,);
     for(int i=;i<n;i++)
     {
         if(i==)
             printf("%d",T[i]);
         else printf(" %d",T[i]);
     }
     return ;
 }