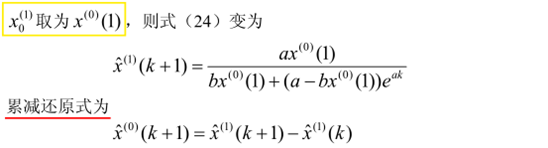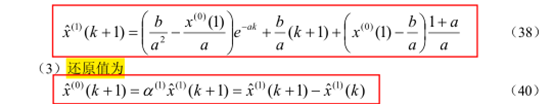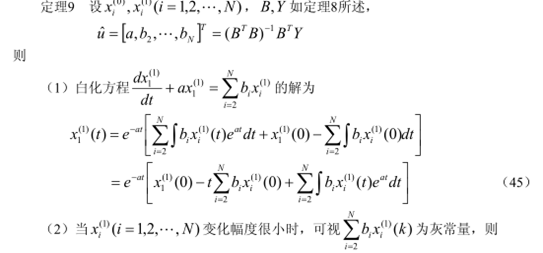【数学建模】灰色系统理论II-Verhulst建模-GM(1,N)-GM(2,1)建模
灰色系统理论中,GM(1,1)建模很常用,但他是有一定适应范围的。
GM(1,1)适合于指数规律较强的序列,只能描述单调变化过程。对于具有一定随机波动性的序列,我们考虑使用Verhulst预测模型,或者GM(2,1)模型。
Verhulst和GM(2,1)适合于非单调的摆动发展序列或者具有饱和状态的 S 形序列。
Verhulst预测模型
Verhulst模型的定义如下:
对于模型参数,使用最小二乘估计有以下结果:
最终,可以求得灰色Verhulst的解为:
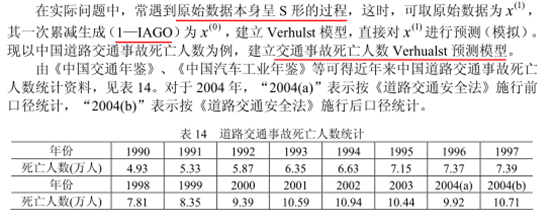
Verhulst模型应用:道路交通事故预测
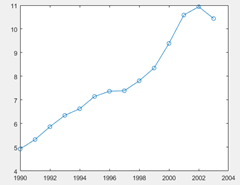
对于交通事故死亡人数统计数据,我们首先做出大体曲线变化图,以从整体上着手。
可见曲线呈现S型,考虑使用verhulst建模。建模过程如下:
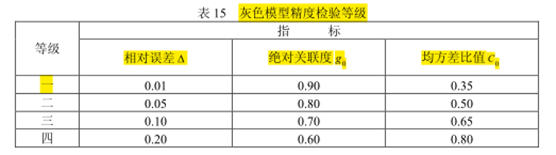
最后我们还要进行一步模型精度检验。灰色模型有一套具体的检验标准,后注。
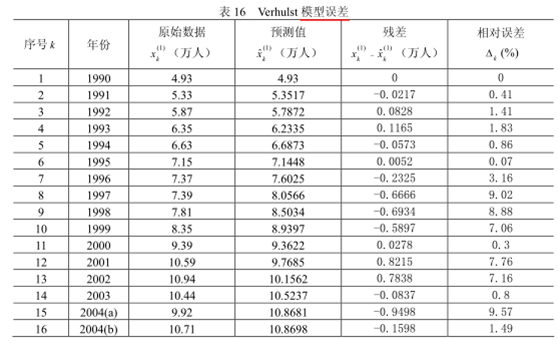
检验三个指标:相对误差、绝对关联度、均方差比值。利用MATLAB检验结果如下:
可见:
平均相对误差为 3.74% ,则模型精度为二级;同时算得绝对关联度 g 为 0.9845,
均方差比值 C 为 0.2355,则模型精度为一级,可见模型精度较高,可用于事故预测。附MATLAB程序:
clc,clear
x1=[4.93 5.33 5.87 6.35 6.63 7.15 7.37...
7.39 7.81 8.35 9.39 10.59 10.94 10.44];
n = length(x1);
nian=:;
plot(nian,x1,'o-');
x0=diff(x1); %作累减生成
x0=[x1(),x0]
z1=0.5*(x1(:n)+x1(:n-)) %求紧邻均值生成序列
B=[-z1',z1'.^]
Y=x0(:end)'
ab_hat=B\Y %估计参数 a,b 的值
x=dsolve('Dx+a*x=b*x^2','x(0)=x0'); %求解常微分方程
x=subs(x,{'a','b','x0'},{ab_hat(),ab_hat(),x1()}); %代入参数值
yuce=subs(x,'t',:) %计算预测值
%下面显示微分方程的解,为了提高计算精度,把该语句放在计算预测值之后
x=vpa(x,)
x1_all=[x1,9.92,10.71]; %加上 年的两个观测值
yuce()=yuce(); % 年有两个观测值,要对应两个相同的预测值
epsilon=x1_all-yuce %计算残差
delta=abs(epsilon./x1_all) %计算相对误差
delta_mean=mean(delta) %计算平均相对误差
x1_all_0=x1_all-x1_all(); %观测值数据列的始点零化像
yuce_0=yuce-yuce(); %预测值数据列的始点零化像
s0=abs(sum(x1_all_0(:end-))+0.5*x1_all_0(end));
s1=abs(sum(yuce_0(:end-))+0.5*yuce_0(end));
tt=yuce_0-x1_all_0;
s1_s0=abs(sum(tt(:end-))+0.5*tt(end));
absdegree=(+s0+s1)/(+s0+s1+s1_s0) %计算灰色绝对关联度
c=std(epsilon,)/std(x1_all,) %计算标准差比值
灰色预测模型检验标准:
1. 残差合格模型
2. 关联度合格模型
3. 均方差比合格模型
由上可知,给定一组取值,就确定了检验模型精度的一个等级。常用的精度等级见下表:
GM(2,1)模型和DGM模型
1. GM(2,1)模型
弱化算子
对于初期增长势头过于猛烈的模型,为了提高精度,可以考虑使用弱化算子处理原始数列。
对应的,依旧是最小二乘估计参数,再对微分方程求解,得到:
2. DGM(2,1)模型
证明略。
GM(1,N)模型和GM(0,N)模型
1. GM(1,N)
2. GM(0,N)模型
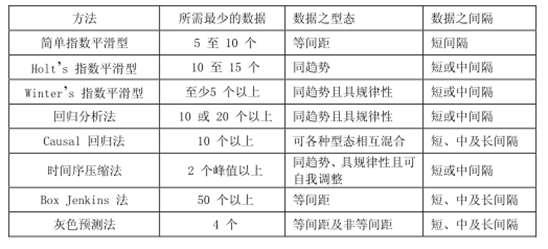
总结:灰色预测法与传统统计方法的比较
【数学建模】灰色系统理论II-Verhulst建模-GM(1,N)-GM(2,1)建模的更多相关文章
- 数学建模-灰色预测模型GM(1,1)_MATLAB
GM(1,1).m %建立符号变量a(发展系数)和b(灰作用量) syms a b; c = [a b]'; %原始数列 A A = [174, 179, 183, 189, 207, 234, 22 ...
- 《Entity Framework 6 Recipes》翻译系列 (5) -----第二章 实体数据建模基础之有载荷和无载荷的多对多关系建模
2-3 无载荷(with NO Payload)的多对多关系建模 问题 在数据库中,存在通过一张链接表来关联两张表的情况.链接表仅包含连接两张表形成多对多关系的外键,你需要把这两张多对多关系的表导入到 ...
- 【数学建模】数模day13-灰色系统理论I-灰色关联与GM(1,1)预测
接下来学习灰色系统理论. 0. 什么是灰色系统? 部分信息已知而部分信息未知的系统,我们称之为灰色系统.相应的,知道全部信息的叫白色系统,完全未知的叫黑色系统. 为什么采用灰色系统理论? 在给定信息不 ...
- 卓金武《MATLAB在数学建模中的应用》 第2版
内容介绍 本书的作者都具有实际的数学建模参赛经历和竞赛指导经验.书中内容完全是根据数学建模竞赛的需要而编排的,涵盖了绝大部分数学建模问题的matlab求解方法.本书内容分上下两篇.上篇介绍数学建模中常 ...
- 2020华为杯数学建模B题-RON建模 赛后总结与分析
好久好久没有写博客了...挺累的,从二月份开始找暑期实习,接着在进行暑期实习,然后马不停蹄地进行秋招,现在总算结束实习,前两天又参加了华为杯数学建模竞赛,感觉接下来就会很轻松了,希望能好好休息休息.这 ...
- Python小白的数学建模课-07 选址问题
选址问题是要选择设施位置使目标达到最优,是数模竞赛中的常见题型. 小白不一定要掌握所有的选址问题,但要能判断是哪一类问题,用哪个模型. 进一步学习 PuLP工具包中处理复杂问题的字典格式快捷建模方法. ...
- 《Entity Framework 6 Recipes》中文翻译系列 (30) ------ 第六章 继承与建模高级应用之多对多关联
翻译的初衷以及为什么选择<Entity Framework 6 Recipes>来学习,请看本系列开篇 第六章 继承与建模高级应用 现在,你应该对实体框架中基本的建模有了一定的了解,本章 ...
- .NET应用架构设计—面向对象分析与设计四色原型模式(彩色建模、领域无关模型)(概念版)
阅读目录: 1.背景介绍 2.问自己,UML对你来说有意义吗?它帮助过你对系统进行分析.建模吗? 3.一直以来其实我们被一个缝隙隔开了,使我们对OOAD遥不可及 4.四色原型模式填补这个历史缝隙,让我 ...
- Smart3D系列教程1之《浅谈无人机倾斜摄影建模的原理与方法》
一.引言 倾斜摄影测量技术是国际测绘遥感领域近年发展起来的一项高新技术,以大范围.高精度.高清晰的方式全面感知复杂场景,通过高效的数据采集设备及专业的数据处理流程生成的数据成果直观反映地物的外观.位置 ...
随机推荐
- css中关于table的相关设置
一.设置好看的单边框表格 1.一种实现方式 分别给table标签和td标签设置不在同一方向的border属性,如下table设置‘左上’边框,td设置‘右下’边框.其他设置方式同样可以实现. tabl ...
- bootstrap-treeview 树形菜单带复选框以及级联选择
<div id="searchTree"></div> <script> var treeData = [{ text: "Paren ...
- 自然底数e的意义是什么?
自然底数e的意义是什么? https://mp.weixin.qq.com/s?__biz=MzA5ODUxOTA5Mg==&mid=2652553811&idx=1&sn=0 ...
- Arcgis瓦片--js客户端加载
接上篇博客,下载好arcgis格式的瓦片数据以后,需要用js客户端在前端加载出来.这里介绍两种方案: 1.使用超图iServer将瓦片发布成rest地图服务,或者arcgis地图服务,客户端直接加载 ...
- linux命令df中df -h和df -i
df 命令: linux中df命令的功能是用来检查linux服务器的文件系统的磁盘空间占用情况.可以利用该命令来获取硬盘被占用了多少空间,目前还剩下多少空间等信息. 1.命令格式: df [选项] [ ...
- electron入坑指南
electron入坑指南 简介 electron 实际集成chrome浏览器和node环境, 运行你写的网页 app 基本目录结构 index.html 名称可以不是index, 这个文件与普通网页的 ...
- UE4分支的Git Flow
UE4作为开源商业引擎,其代码托管在私有库:https://github.com/EpicGames/UnrealEngine 为了能看到并下载UE4的代码,开发者需要有GitHub账号和Unreal ...
- Linux系统下 MySQL 安装 指南(5.7和8.0 版本)
一. 准备工作 1 删除本地centos7中的mariadb: 查看系统中是否已安装 mariadb 服务: rpm -qa | grep mariadb 或 yum list installed | ...
- 2017 百度杯丶春秋欢乐赛 writeup
1. 内涵图(Misc) 题目: 我不是一个简单的图片 我是一个有内涵的图片 解:保存到桌面,右键属性->详细信息,即可获得flag. 2. 小电影(Misc) 题目: 我说过 这次比赛是让大家 ...
- 【English】20190321
Keep in mind记住[kip ɪn maɪnd] maintenance维护[ˈmentənəns] Also Keep in mind that table maintenance use ...