BUAA-OO第一单元小结

引言

四周过去了，oo课程的第一阶段作业也算告一段落。在第一单元的内容中，主题是始终如一的多项式求导，但三次作业要求完善的求导功能一次比一次丰富，难度也逐渐增加，也是费了不少心思。接下来就回顾与小结一下这三次作业，分析一下程序结构、遇到的bug以及总结这第一单元作业给我的感受。

第一次作业（关于幂函数多项式求导）

类图：

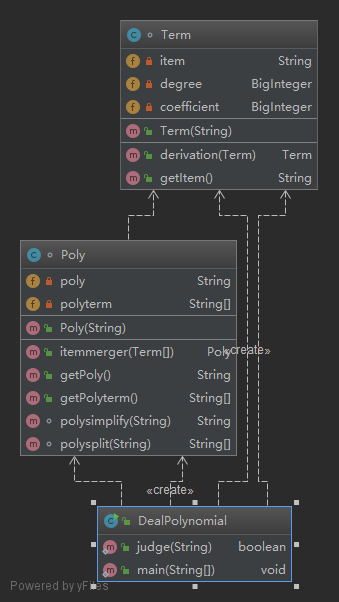度量分析：

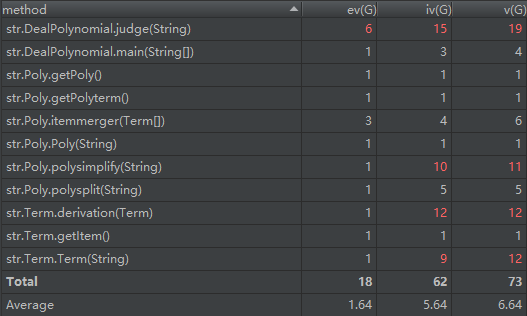
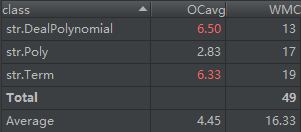程序分析：

由于是第一次作业对于面向对象了解不是很透彻，只是根据面向对象的教材依葫芦画瓢创建了两个类，Term类完成项的求导，Poly类完成多项式的求导。但显然类的封装性并不好，并且class内部的架构考虑的不是很清楚。

但由于第一次作业比较简单，并且当时没有考虑到性能的问题，并没有对多项式进行化简的处理，因此整体程序较为简单。

Bug分析：

第一次作业最困扰我的是多项式判定的问题，一开始采用一个正则表达式判定多项式的正确性，但是发现过于暴力，程序会爆栈，于是又费尽心机使用多种方法判定多项式的正确性。但是由于考虑不全面，互测时几乎全部都是由于多项式判定考虑不全面的bug。

而关于找寻别人的bug，我主要采取阅读代码与测试数据一起进行的方式，在测试数据时进行代码阅读，找出可能的bug。但是主要找到的bug大部分还是因为多项式判定的问题。

第二次作业（关于幂函数与三角函数相乘的多项式求导）

类图：

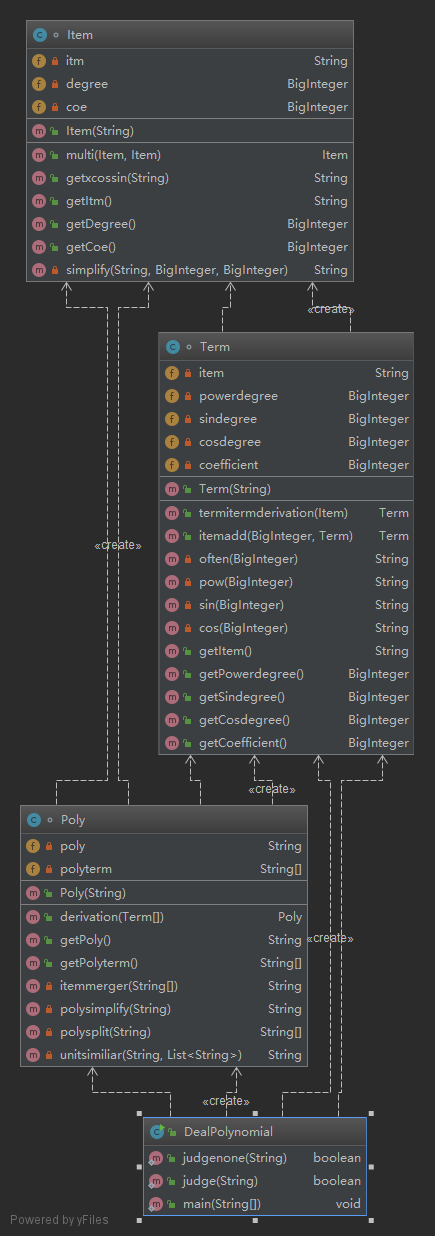
度量分析：

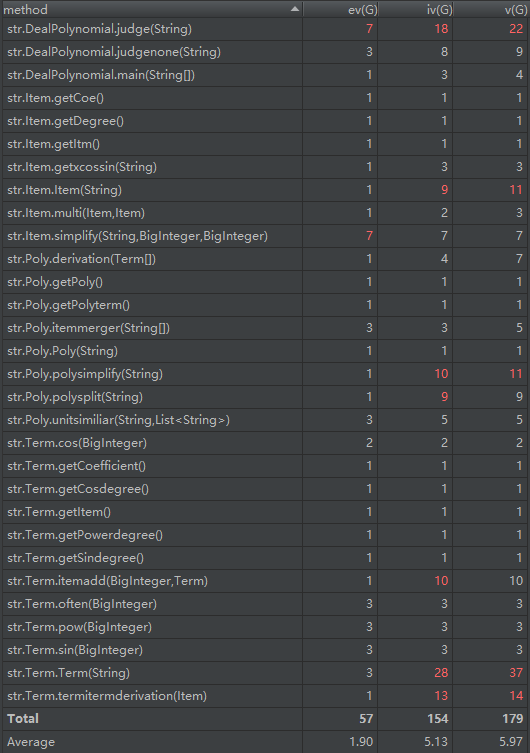
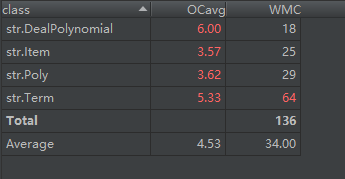
程序分析：

这一次作业应该是上次作业里最不满意的一次，甚至因为这一次作业非常混乱的逻辑，导致第三次作业进行了大篇幅的重构。这一次作业由于吸取了第一次作业没有化简多项式，导致代码复杂度很高的问题，在修改第一次作业的同时，增加了合并同类项这样的功能。为了化简多项式，我的思路是对要求导的多项式进行化简，求完导后再进行一次化简。于是我将化简写入了Poly类的构造器部分，产生了每次构造一个多项式都要进行化简的问题，使得代码逻辑混乱。

Bug分析：

由于第一次作业的教训，加上第二次作业在中测时就进行了大部分的多项式判定测试，在多项式判定的部分bug就少了很多。主要的bug是在多项式化简的问题上，很多细节没有考虑到位。包括有时候会因为字符串和数组大小的问题，使得程序RUNTIME_ERROR。

在对别人的代码进行测试的时候，由于作业代码量比第一次明显偏大，所以主要采用测试数据的方式。但是发现的bug仅仅停留在多项式判定上，并且大部分是因为化简的问题。

第三次作业（关于幂函数与三角函数的复合函数多项式求导）

类图：

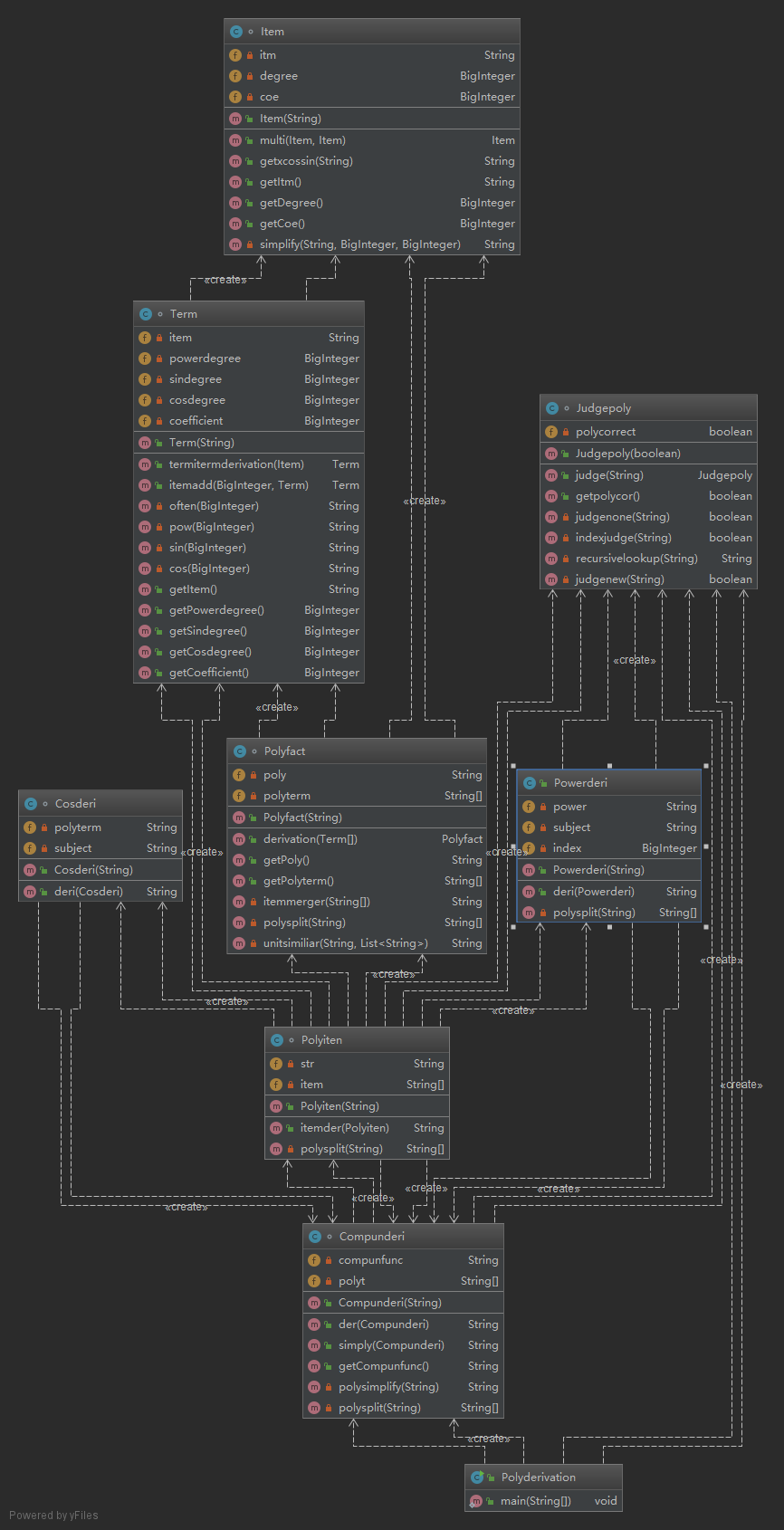
度量分析：

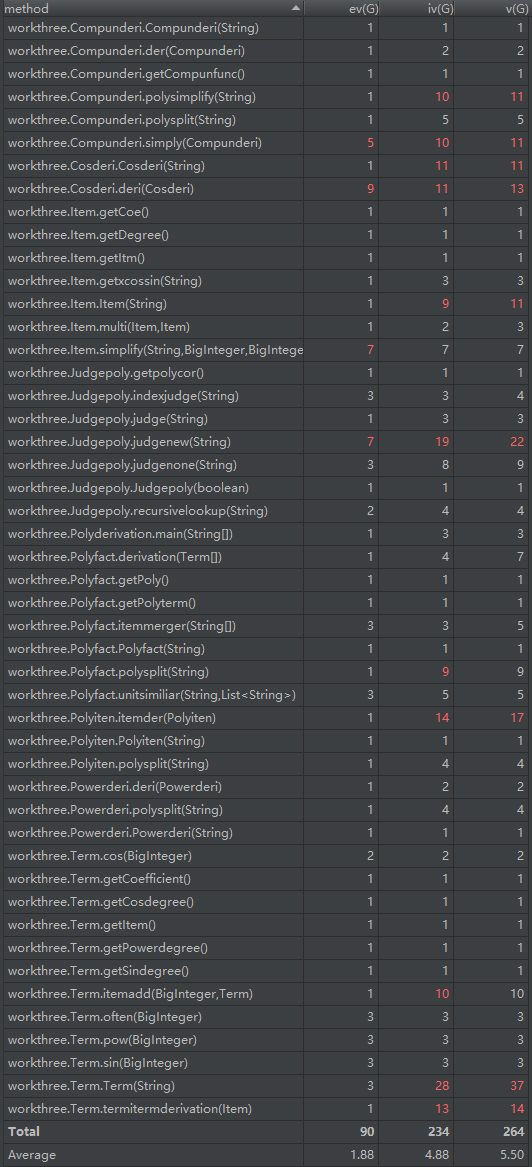
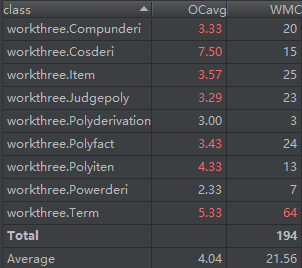
程序分析：

由于第二次作业失败的多项式化简以及代码逻辑混乱，再加上对于类的理解的深入，我对第三次代码进行了大范围的重构，包括多项式的判定，幂函数、三角函数求导，复合函数求导等，我一一构造类来完成这些功能，然后完成项的求导类，最后再将他们运用到多项式类里，完成一个多项式求导。这一次作业性能分占比较小，因此我并没有考虑，仅仅实现了求导的功能。实际上这一次作业代码内在逻辑很容易理顺，但是如果遇上疯狂递归，运行时间较长。

Bug分析：

这一次作业同样在多项式判定上没有问题，但由于很多小细节被忽略，导致代码错误较多。比方说因为没有考虑到+/-()这样的形式造成的问题，再比如在最后化简输出时没有考虑到输出多项式长度只有1的可能等等。而这些细节错误，主要还是由于自己的测试数据不够全面，自己应该认识到仅仅过中测是不够的。

在互测阶段，由于这次的代码需要考虑递归，可以说看别人的代码找bug是比较费时费力的，因此我还是采用测试数据的方式进行，但是不大理想。

第一单元总结

在这一阶段的代码编辑过程中，对于面向对象有了一定的了解，对于一个类的编辑，还是有了一些体会，特别是构造器，在三次作业中类的构造器，逐渐简化，不会再出现第二次作业那种每次构造一个类就要进行很复杂的操作这样子。但是显然，对于面向对象，我还有很多方面不是很清晰，特别是继承这一块，还并不了解。

考虑代码的重构，对于第三次作业，我可能会将最后一部分x以及常数求导那里因为偷懒直接放上第二次作业代码，对这部分进行化简；并且加上求导结果简化的代码，完善代码风格。而第二次作业，我会考虑将化简与构造器分离。

虽然经过这三次作业对于面向对象有了一定的了解，特别是类的封装的部分，但是对于其他的了解还不够深入，因此希望在今后的学习中，能加深自己对于面向对象的了解。