SA：T1编写主函数法和T2Matlab自带的SA工具箱GUI法，两种方法实现对二元函数优化求解——Jason niu

%SA：T1法利用Matlab编写主函数实现对定义域[-5,5]上的二元函数求最优解—Jason niu
[x,y] = meshgrid(-5:0.1:5,-5:0.1:5);
z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20;
figure
mesh(x,y,z)
hold on
xlabel('x')
ylabel('y')
zlabel('z')
title('SA：利用SA最优化，定义域[-5,5]上的二元函数z =  x^2 + y^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20的最大值—Jason niu')

maxVal = max(z(:));
[maxIndexX,maxIndexY] = find(z == maxVal);
for i = 1:length(maxIndexX)
    plot3(x(maxIndexX(i),maxIndexY(i)),y(maxIndexX(i),maxIndexY(i)), maxVal, 'r*','linewidth',2)
     text(x(maxIndexX(i),maxIndexY(i)),y(maxIndexX(i),maxIndexY(i)), maxVal, {['    X: ' num2str(x(maxIndexX(i),maxIndexY(i)))];['    Y: ' num2str(y(maxIndexX(i),maxIndexY(i)))];['    Z: ' num2str(maxVal)]})
    hold on
end

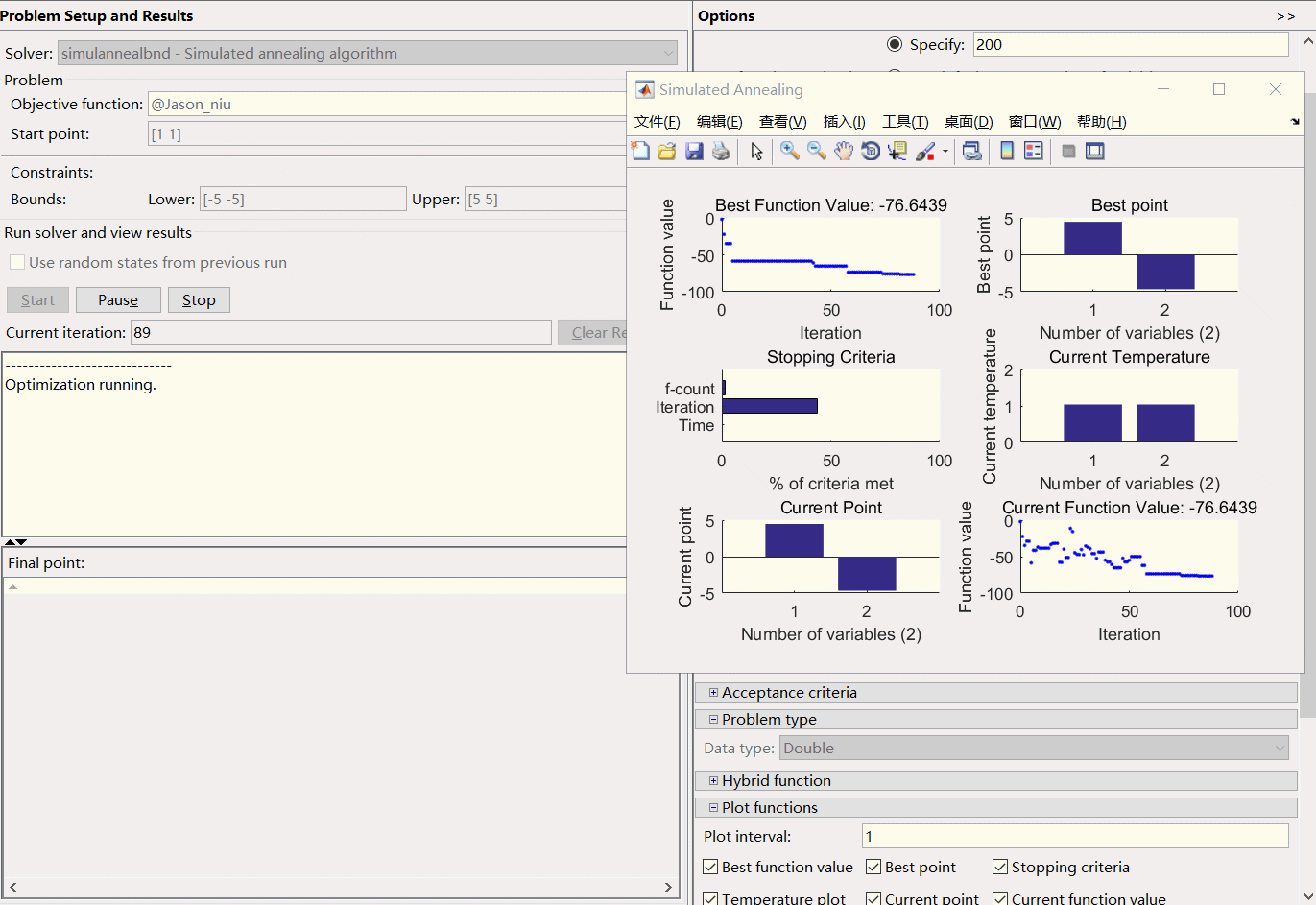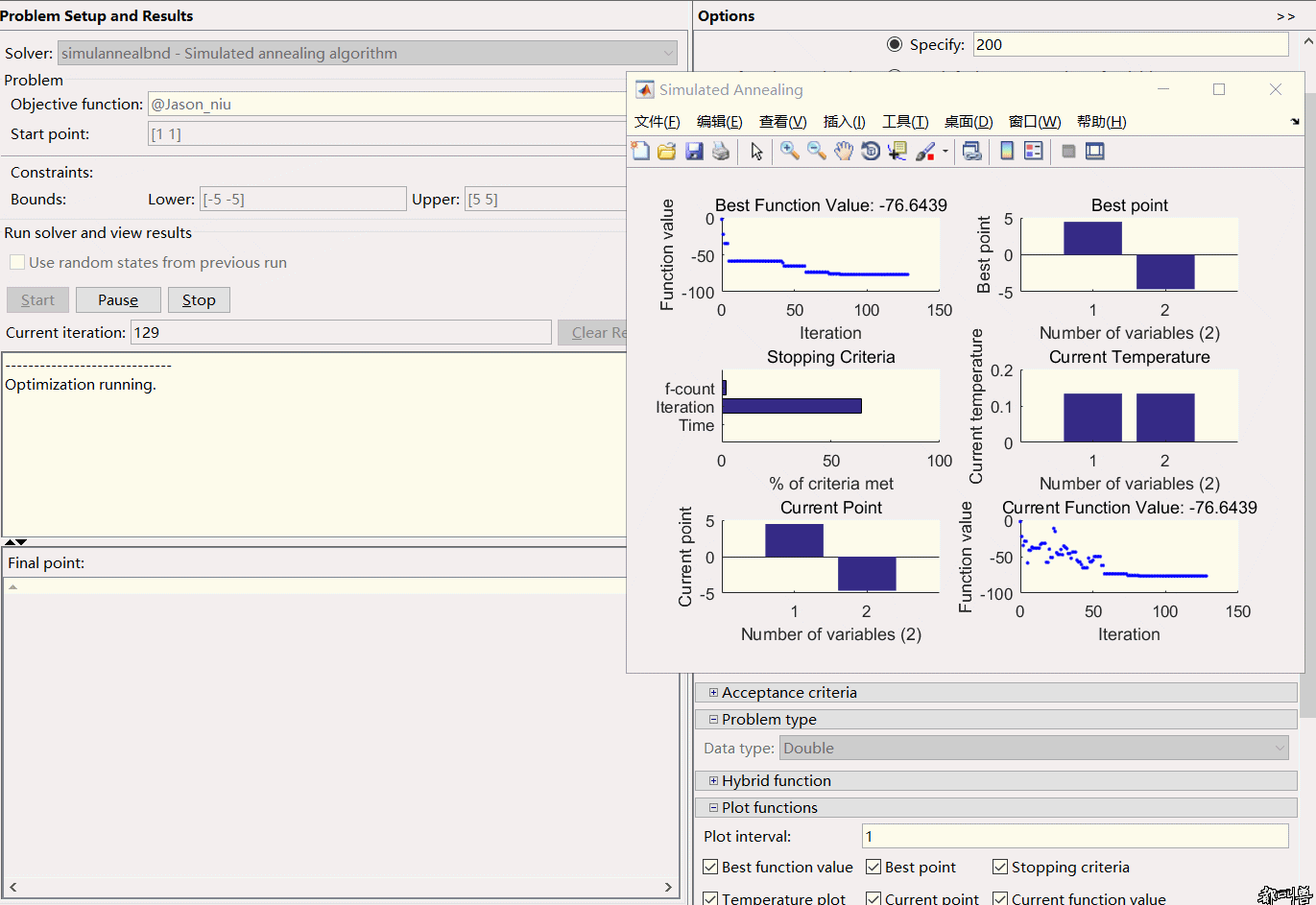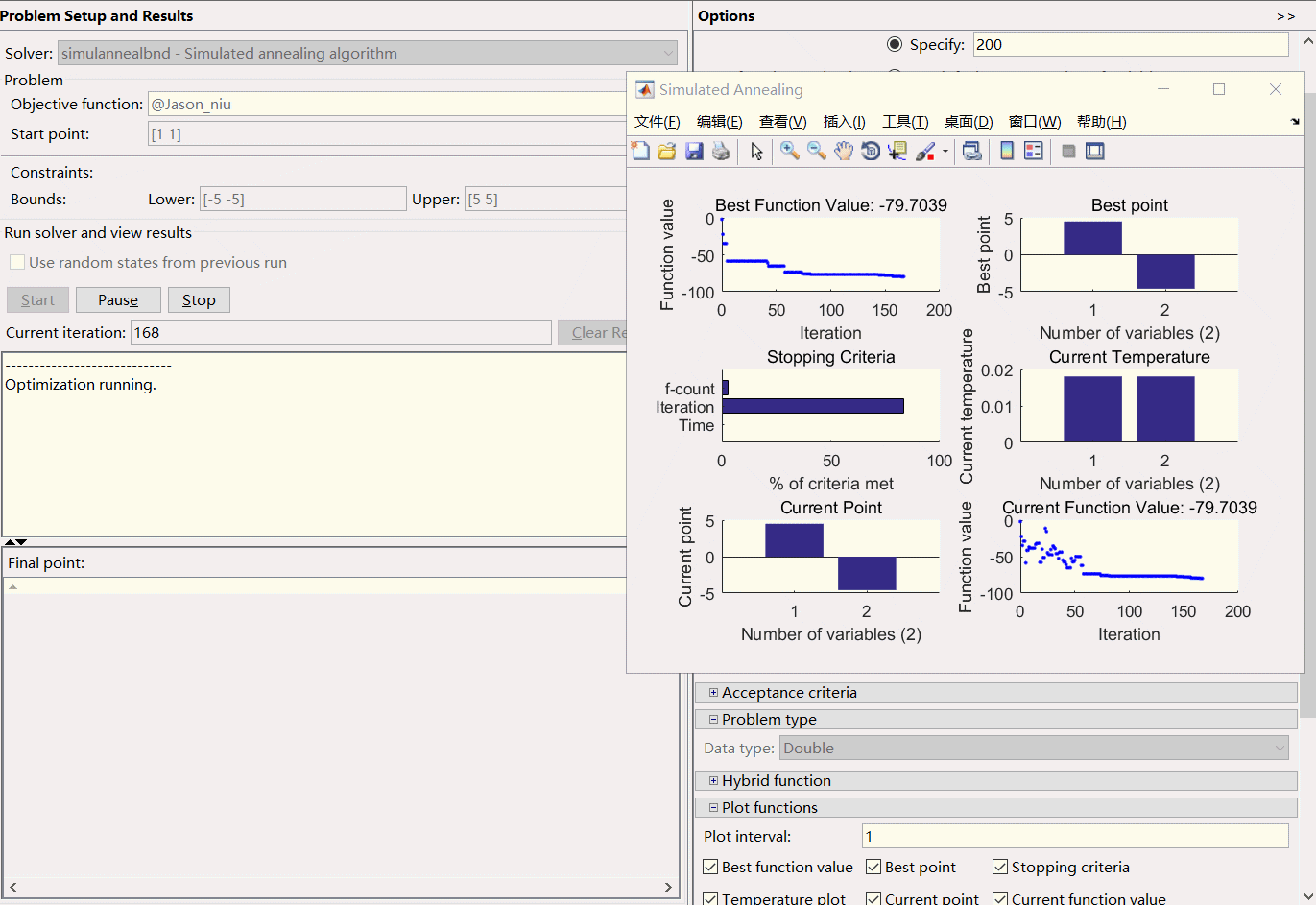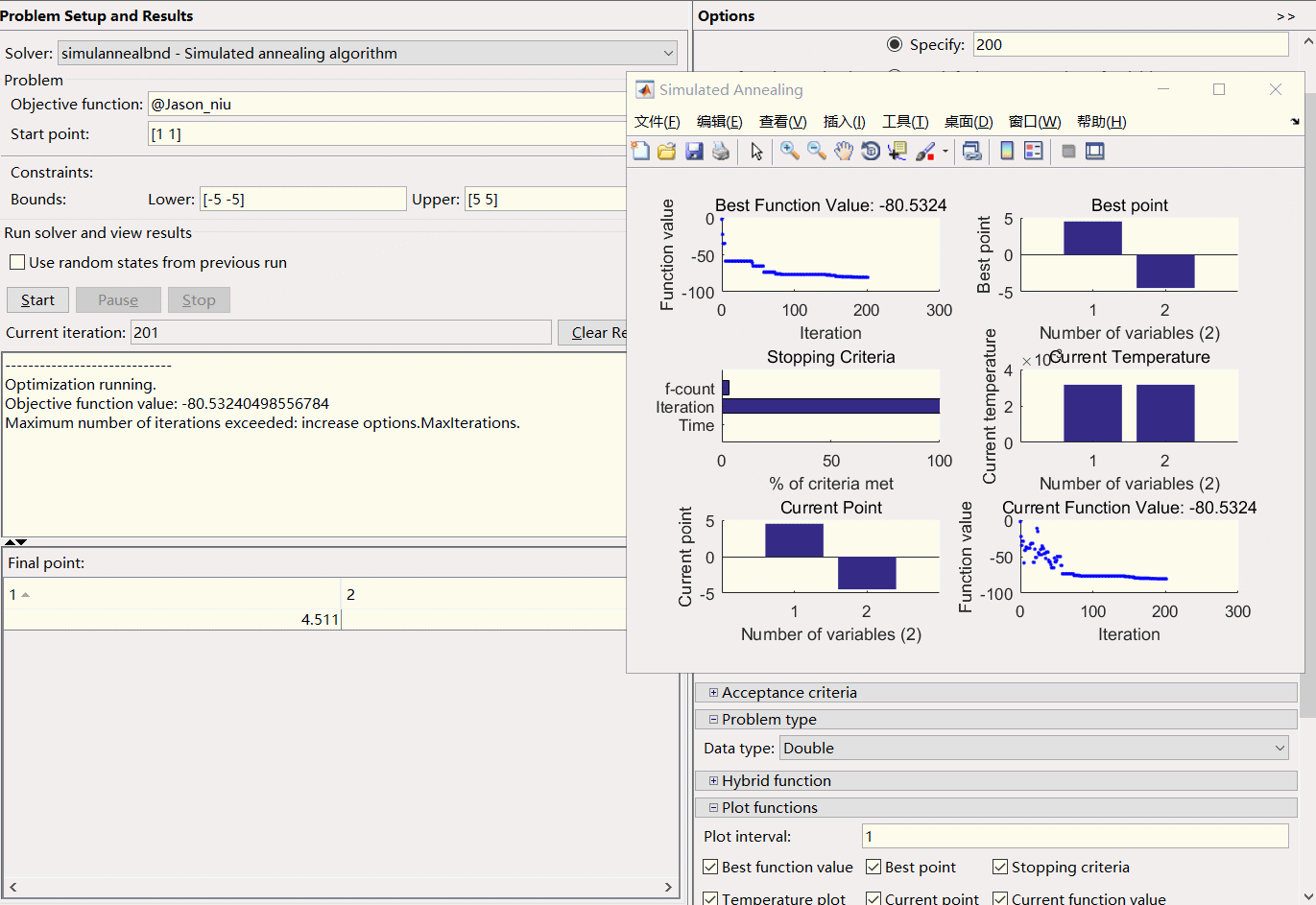
%SA：T2法利用Matlab自带的SA工具箱optimtool通过GUI调用@Jason_niu函数实现对二元函数优化求解—Jason niu
function fitnessVal = Jason_niu( x )